神经网络，手写数字识别，学习笔记

参考资料

wzy 的博客：https://blog.csdn.net/WAautomaton/article/details/108542706?spm=1001.2014.3001.5501
Nueral Networks and Deep Learning（网上可以下）
3Blue1Brown 的视频：https://www.bilibili.com/video/BV1bx411M7Zx
MNIST 的数据：http://yann.lecun.com/exdb/mnist/

神经网络

类似人类神经元，建立了若干层结点，相邻层有连边
边上有系数（表示上一层基底对下一层的影响）
下一层的值 \(d_i=\sum_{j}w_{j,i}v_j+c_i\)（最后映射到 \([0,1]\)）
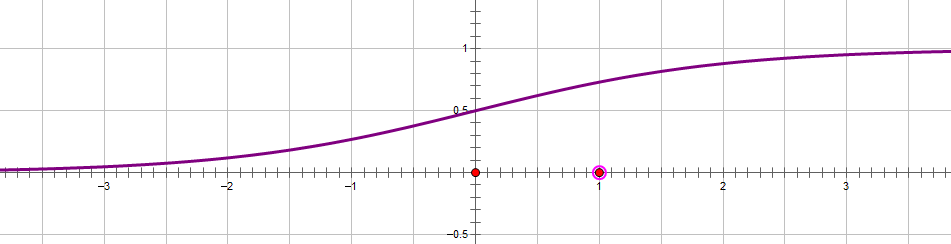
我们需要找到一个连续的函数来完成这个映射，sigmod 函数 \(\frac 1{1+e^{-x}}\)，即 \(v_i=sigmod(d_i)\)

我们要做的就是分配系数，使得对于所有数据，输出向量和我们想要的尽量接近
用估价函数 \(E=\sum_{i=0}^9(v_i-a_i)^2\) 来刻画（希望是 \(a\)），那么如何分配系数使其最小化呢
我们求出偏导 \(\frac{\partial E}{\partial v_i}\)，那么我们希望 \(v\) 朝向量 \((\frac{\partial E}{\partial v_1},\frac{\partial E}{\partial v_2},\dots)\) 的方向移动一小步
我们知道，\(E\) 是关于 \(w_{i,j},c_i\) 的多元函数，我们希望求出 \(\frac{\partial E}{\partial w_{i,j}},\frac{\partial E}{\partial c_i}\)
\(\frac{\partial E}{\partial c_i}=\frac{\partial E}{\partial d_i}\)，我们只需要求出 \(\frac{\partial E}{\partial d_i}\)
而由链式法则：\(\frac{\partial E}{\partial d_i}=\frac{\partial E}{\partial v_i}\frac{\partial v_i}{\partial d_i}\)，后者即为 \(v_i(1-v_i)\)
这样我们就算出了最后一层的 \(\frac{\partial E}{\partial d_i}\)
考虑到 \(d_i=\sum_j w_{j,i}v_j\)，故 \(\partial d_i=\sum_j w_{j,i}\partial v_j\)（将 \(w\) 看成常数）
那么 \(\frac{\partial E}{\partial v_i}=\sum_j w_{i,j}\frac{\partial E}{\partial d_j}\)
算出这个过后就能算出 \(\frac{\partial E}{\partial d_i}\)
考虑计算 \(\frac{\partial E}{\partial w_{i,j}}\)，注意到 \(d_i=\sum_j w_{i,j} v_j\)
故 \(\frac{\partial d_j}{\partial w_{i,j}}=v_i\)，\(\frac{\partial E}{\partial w_{i,j}}=v_i\frac{\partial E}{\partial d_j}\)
最后我们只需要将所有值移动一点距离（具体来讲，如 \(w_{i,j}\) 减去 \(\eta v_i\frac{\partial E}{\partial d_j}\)，实现中我的 \(\eta\) 设的是 0.1）
把数据喂进去不断迭代就可以找到较优的系数

Code(c++)

我写了两份，一份读入图片和数字，输出迭代好的系数
第二份读入系数和图片，输出数字，和答案进行比对
网络隐藏层用了 64 个结点
code1
code2
学习 6w 个数据用了大约 5 min，正确率达到了 \(\%95.94\)