高中数学

Author : ArrowHaru

目录

• 解析几何
  • 圆锥曲线
    • 圆
    • 椭圆
      • 焦半径
      • 焦点三角形
      • 第二定义
      • 中点弦
    • 抛物线
      • 两点式与平均性质
        • 两点式
        • 平均性质
    • 切线
    • 好题

解析几何

圆锥曲线

圆

椭圆

主要讨论焦点在 \(x\) 轴上的情况。

用 \(F_1(F_2)\) 表示左（右）焦点（focus），\(P(x_0, y_0)\) 表示椭圆上任意一点。

焦半径

\(|PF_1| = a + ex_0, |PF_2| = a - ex_0\)。\(|PF_{1/2}| \in [c - a, c + a]\)。

\(P(x, y)\) 为椭圆上任意一点，有 \(|PF_1| = \sqrt{(x + c)^2 + y^2}, |PF_2| = \sqrt{(x - c)^2 + y^2}\)。

\(\begin{cases}|PF_1|+|PF_2| = 2a\\|PF_1|^2 - |PF_2|^2 = 4cx\end{cases}\Longrightarrow |PF_1| - |PF_2| = \dfrac{2cx}{a}\Longrightarrow |PF_1| = a + \dfrac{c}{a}x,|PF_1| = a - \dfrac{c}{a}x\)。

焦点三角形

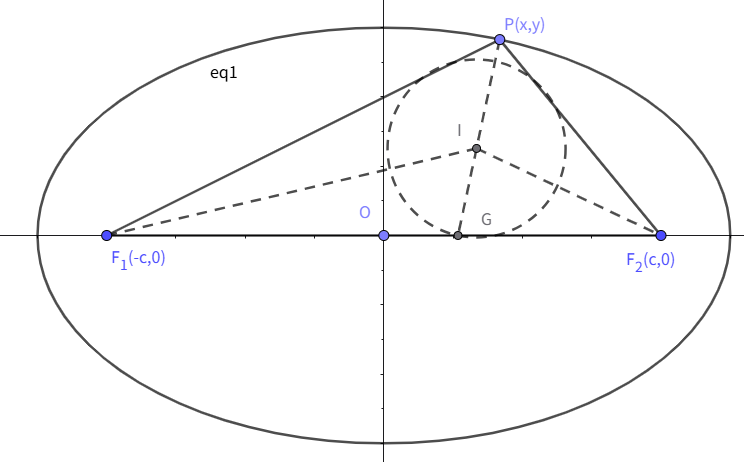
如图 \(P(x, y)\) 为椭圆上异于左右顶点上的一点，\(\triangle PF_1F_2\) 为椭圆的焦点三角形。记 \(\theta = \angle F_1PF_2\)。

1. 周长：\(C = |PF_1| + |PF_2| + |F_1F_2| = 2a + 2c\)。

2. 面积：\(S = b^2\tan \dfrac{\theta}{2}\)。

   对 \(\triangle F_1PF_2\) 用余弦定理可以得到 \(|PF_1|\cdot|PF_2| = \dfrac{2b^2}{1+\cos \theta}\)。

   故 \(S_{\triangle PF_1F_2} = |PF_1|\cdot|PF_2|\cdot\sin \theta /2 = b^2\tan \dfrac{\theta}{2}\)。

3. 内心：\(I\) 为 \(\triangle PF_1F_2\) 内心。

   在 \(\triangle PF_1F_2\) 中，由正弦定理可得\(\dfrac{|PF_1|}{|GF_1|}=\dfrac{|PF_2|}{|GF_2|} = \dfrac{|PF_1|+|PF_2|}{|GF_1|+|GF_2|}=\dfrac{a}{c}\)。

   在 \(\triangle PF_1G\) 中，由角平分线定理可得 \(\dfrac{|PI|}{|IG|} = \dfrac{|PF_1|}{|GF_1|} = \dfrac{|PF_2|}{|GF_2|} = \dfrac{a}{c}\)。

4. \(e\in[\sin\dfrac{\theta}{2},1)\)。

   由 \(S_{\triangle PF_1F_2} = b^2\tan \dfrac{\theta}{2} = c|y|\) 可得，当 \(|y| = b\) 时，\(\tan \dfrac{\theta}{2}\) 最大 \(\Longleftrightarrow \sin\dfrac{\theta_{\max}}{2} = \dfrac{c}{a} = e \ge \sin\dfrac{\theta}{2}\)。

5. 离心率公式：设 \(\angle PF_1F_2 = \alpha, \angle PF_2F_1 = \beta\),则 \(e = \dfrac{c}{a} = \dfrac{|F_1F_2|}{|PF_1|+{|PF_2| }} = \dfrac{\sin(\alpha+\beta)}{\sin\alpha+\sin\beta}\)。

第二定义

平面上到定点（焦点）与到定直线（准线（Diretirx））的距离之比为常数 \(e\) 的点的轨迹是椭圆。

左准线\(D_1\)：\(x = -\dfrac{a^2}{c}\)，右准线 \(D_2\) ：\(x = \dfrac{a^2}{c}\)。即 \(\dfrac{|PF_1|}{\mathrm{Dis}(F_1, D_1)} =\dfrac{|PF_2|}{\mathrm{Dis}(F_2, D_2)} = e\)。

\(|PF_1| = a + \dfrac{c}{a}x =\dfrac{c}{a}(x + \dfrac{a^2}{c})= \sqrt{(x + c)^2 + y^2} \Longleftrightarrow\) \(\dfrac{|PF_1|}{\mathrm{Dis}(P,x = -\dfrac{a^2}{c})} = e\)，同理 \(\dfrac{|PF_2|}{\mathrm{Dis}(P,x = \dfrac{a^2}{c})} = e\)。

中点弦

抛物线

两点式与平均性质

讨论抛物线 \(y^2 = 2px\) 上有 \(A(x_1, y_1), B(x_2, y_2)\) 时的性质。

两点式

推导可得：

• 对于 \(y^2 = 2px, l_{AB}:(y_1+y_2)y=2px +y_1y_2\)。

• 对于 \(x^2 = 2py,l_{AB}:(x_1+x_2)x=2py +x_1x_2\)。

平均性质

设直线 \(AB\) 与 \(x\) 轴交于 \(M(x_0, 0)\)。\(x_1x_2 = x_0^2, y_1y_2 = -2px_0\)。

\(M\) 代入 \(l_{AB}\) 中，得 \(y_1y_2 = -2px_0\Longleftrightarrow \begin{cases}y_1^2y_2^2=4p^2x_0^2\\y_1^2 = 2px_1\\y_2^2 = 2px_2\end{cases}\Longleftrightarrow x_1x_2=x_0^2\)。

同理，对于 \(x^2 = 2py,M(0, y_0),x_1x_2 = -2py_0, y_1y_2 = y_0^2\)。

切线

记 \(P(x_0, y_0)\) 为圆锥曲线上一点，求过点 \(P\) 的切线 \(l\)。

• 圆：\(l:(x_0-a)(x-a)+(y_0-b)(y-b)=r^2\)。

• 椭圆：\(l : \dfrac{x_0}{a^2}x+\dfrac{y_0}{b^2}y=1\)。

• 双曲线：\(l : \dfrac{x_0}{a^2}x-\dfrac{y_0}{b^2}y=1\)。

• 抛物线：\(l:y_0y=x+x_0\)。

证明以椭圆为例。

证法一：

好题

1. 设抛物线 \(C:y^2 = 2px(p>0)\) 的焦点为 \(F\)，点 \(D(p, 0)\)，过 \(F\) 的直线交 \(C\) 于 \(M, N\) 两点，当直线 \(M\!D\) 垂直于 \(x\) 轴时，\(|M\!F| = 3\)。

   1. 求 \(C\) 的方程
   2. 设直线 \(M\!D, C\!D\) 与 \(C\) 的另一个交点分别为 \(A, B\)，记直线 \(M\!N, A\!B\) 的倾斜角分别为 \(\alpha, \beta\)，当 \(\alpha - \beta\) 取最大值时，求直线 \(A\!B\) 的方程

   1. 由焦半径公式得 \(p + p/2 = 3 \Rightarrow p = 2\Rightarrow C:y^2 = 4x\)。

   2. 设直线 \(AB\) 与 \(x\) 轴相交于 \(P(x_0, 0),M(x_1, y_1), N(x_2, y_2), A(x_3, y_3), B(x_4, y_4)\)。

      由抛物线的平均性质可得：\(y_1y_2 = -4,y_1y_3=-8, y_2y_3 = -8\Rightarrow y_1y_2y_3y_4 = 64\Rightarrow y_3y_4 = -16\Longleftrightarrow AB\) 过定点 \((4, 0)\)。

      1. \(M\!N \perp x\) 轴，\(A\!B \perp x\) 轴，故\(\alpha - \beta = 0\)。

      2. \(k_{M\!N} = \dfrac{y_1 - y_2}{x_1 - x_2}=\dfrac{4}{y_1+y_2},k_{AB} = \dfrac{4}{y_3+y_4} = \dfrac{4}{\frac{-8}{y_1}+\frac{-8}{y_2}} = \dfrac{y_1y_2}{-2(y_1 + y_2)} = \dfrac{2}{y_1+y_2}\)。

         \(k_{M\!N} = 2k_{A\!B} \Rightarrow \alpha,\beta\) 同为锐角或钝角 \(\Rightarrow \alpha - \beta \in\big[0, \dfrac{\pi}{2}\big)\)。

         \(\tan(\alpha - \beta) = \dfrac{1}{\dfrac{1}{k_{AB}} + 2k_{AB}}\le \dfrac{1}{2\sqrt{2}}\)，当且仅当 \(k_{A\!B} = \dfrac{\sqrt{2}}{2}\) 取等号。

      故 \(l_{AB}: x - \sqrt{2}y - 4 = 0\)。

2. 已知抛物线 \(C:y^2=2px\) 的焦点为 \(F(1,0)\)，过点 \(M(5,0)\) 且斜率为 \(k\) 的直线 \(l\) 与 \(C\) 交于 \(A, B\) 两点，若 \(\triangle F\!A\!B\) 的外心 \(N\) 在 \(x\) 轴上，则直线 \(l\) 的斜率等于（）

   A. \(\pm \sqrt{3}\) B. \(\pm \dfrac{1}{2}\) C. \(\pm\dfrac{\sqrt{3}}{3}\) D. \(\pm2\)

   解法一

   由题意 \(y^2=4x\)，设直线 \(l : k(x-5)=y,A(x_1,2\sqrt{x_1}),B(x_2,2\sqrt{x_2})\).

   \(\begin{cases}y=k(x-5)\\y^2=4x\end{cases}\Rightarrow k^2x^2-(10k^2+4)x+25k^2=0\Rightarrow x_1x_2=25,x_1+x_2=\dfrac{10k^2+4}{k^2}\).

   \(k_{F\!A}=\dfrac{2\sqrt{x_1}}{x_1-1}\)，由题 \(F\!A\) 的中垂线 \(l_1:-\dfrac{x_1-1}{2\sqrt{x_1}}\left(x-\dfrac{x_1+1}{2}\right)=y-\sqrt{x_1}\).

   \(l_1\) 与 \(x\) 轴相交于 \(\left(\dfrac{2x_1}{x_1-1}+\dfrac{x_1+1}{2},0\right)\).同理 \(FB\) 的中垂线 \(l_2\) 与 \(x\) 轴相交于 \(\left(\dfrac{2x_2}{x_2-1}+\dfrac{x_2+1}{2},0\right)\).

   显然，两点应该重合，有\(\dfrac{2x_1}{x_1-1}-\dfrac{2x_2}{x_2-1}=\dfrac{x_2-x_1}{2}\Rightarrow \dfrac{10k^2+4}{k^2}=22\Rightarrow k=\pm\dfrac{\sqrt{3}}{3}\)，故选 D.

   解法二

   设点 \(N(n,0)\)，则 \(\odot N\) 外切 \(\triangle F\!A\!B\)，设 \(\odot N:(x-n)^2+y^2=(n-1)^2\).

   联立 \(\begin{cases}(x-n)^2+y^2=(n-1)^2\\y^2=4x\end{cases}\)，得 \(x^2-(2n-4)x+2n-1=0\).

   联立 \(\begin{cases}y=k(x-5)\\y^2=4x\end{cases}\)，得 \(x_1x_2=25,x_1+x_2=\dfrac{10k^2+4}{k^2}\).

   可得 \(n = 13, k = \pm\dfrac{\sqrt{3}}{3}\)，故选 D.

   显然，解法二的计算量不大，三个图形比两个图形更好刻画。当然，可以每一个试过去