数论专题

组合数学核心概念：第二类斯特林数与球盒模型

整理核心公式与模型，清晰呈现组合计数逻辑

一、第二类斯特林数（\(\left\{ n \atop m \right\}\) / \(S_2(n,m)\)）

定义：\(n\) 个不同元素放入 \(m\) 个非标号、非空盒子的方案数（盒子无区别，不可空）

1. 递推关系

\[\left\{ n \atop m \right\} = \left\{ n-1 \atop m-1 \right\} + m \cdot \left\{ n-1 \atop m \right\} \]

• 解释：第 \(n\) 个元素单独放新盒（对应 \(\left\{ n-1 \atop m-1 \right\}\) ），或放进已有 \(m\) 个盒之一（对应 \(m \cdot \left\{ n-1 \atop m \right\}\) ）

2. 容斥公式

\[\left\{ n \atop m \right\} = \frac{1}{m!} \sum_{i=0}^m (-1)^{m-i} \binom{m}{i} \cdot i^n \]

• 思路：用容斥原理计算“恰好 \(m\) 个非空盒”的方案数（总放法 \(-\) 至少空1盒 \(+\) 至少空2盒 \(\dots\) ）

3. 贝尔数（Bell Number）

\(n\) 个元素所有划分方式的总数（盒子可空、非标号）：

\[B(n) = \sum_{i=0}^n \left\{ n \atop i \right\} \]

二、球盒模型汇总（\(n\) 球，\(m\) 盒）

按球是否不同、盒是否不同分类，整理核心场景与公式：

模型条件（球、盒是否不同）	具体限制	方案数公式/思路
球不同，盒不同	无限制	\(m^n\)（每个球独立选盒）
	盒中至多1个球	\(\dbinom{m}{n} \cdot n! = P(m,n)\)（排列：选 \(n\) 盒放球并排列）
	盒中至少1个球	\(\sum_{i=0}^m (-1)^i \binom{m}{i} (m-i)^n\)（容斥：总放法 \(-\) 至少空盒的情况）
球不同，盒相同	无限制	\(\sum_{i=0}^m \left\{ n \atop i \right\}\)（所有非空划分方式求和）
	盒中至多1个球	\(1\)（仅当 \(n \leq m\)，等价“单元素/空集划分”，无区别时仅1种）
	盒中至少1个球	\(\left\{ n \atop m \right\}\)（直接对应第二类斯特林数定义）
球相同，盒不同	无限制	\(\dbinom{n+m-1}{m-1}\)（隔板法：\(n\) 球排开，\(m-1\) 个板分 \(m\) 组）
	盒有容量限制（如 \(x_i \leq A\) 或 \(x_i \geq B\)）	容斥调整隔板法（减去/补充超过限制的情况）
球相同，盒相同	无限制	动态规划：\(f(n,m) = f(n-1,m-1) + f(n-m,m)\)（最后一盒放1个球，或放至少1个球转化为“\(n-m\) 球放 \(m\) 盒”）；关联五边形数定理，用于整数分拆计数

三、补充关联

• 公式关联：\(m^n = \sum_{i=0}^m \binom{m}{i} \cdot i! \cdot \left\{ n \atop i \right\}\)
  （解释：球不同、盒不同的总放法 = 选 \(i\) 个非空盒 \(\times\) 排列球进盒 \(\times\) 第二类斯特林数划分 ）
• 置换（Permutation）：与斯特林数共同用于组合计数（如划分后排列盒子场景）

核心逻辑：通过“元素是否可区分、容器是否可区分”分类，用斯特林数、容斥原理、隔板法、动态规划覆盖所有组合分配场景，是组合计数的基础框架。

欧拉函数

定义

\(\varphi(n)\) 定义为小于 \(n\) 与 \(n\) 互质的数的个数。 定义 \(\varphi(1)=1\)。

即可得 \(\Large\sum\limits_{i=1}^{n}[\gcd(i,n)=1]=\varphi(n)\)。

例题：P1390 公约数的和

给定 \(n\)，求 $$\large\sum_{i = 1}^n \sum_{j = i + 1}^n \gcd(i, j)$$

\[\large\sum_{i = 1}^n \sum_{j = i + 1}^n \gcd(i, j)\\ =\large\sum_{i = 1}^n \sum_{j = i + 1}^n \sum_{d=1}^{n}d[\gcd(i, j)=d]\\ =\large\sum_{i = 1}^n \sum_{j = i + 1}^n \sum_{d=1}^{n}d[\gcd(\frac{i}{d}, \frac{j}{d})=1]\\ =\sum_{d=1}^{n}d\large\sum_{i = 1}^{\frac{n}{d}} \sum_{j = i + 1}^{\frac{n}{d}} [\gcd(i, j)=1]\\ =\sum_{d=1}^{n}d((\sum_{i=1} ^{\frac{n}{d}}\varphi(i))-1) \]

2

例题：P2303 [SDOI2012] Longge 的问题

给定 \(n\) 求 \(\large\sum\limits_{i=1}^{n}\gcd(i,n)\) , \(1\le n \le 2^{31}-1\)。

\[枚举\gcd(i,n) 的 值:\\ \large\sum\limits_{i=1}^{n}\gcd(i,n)=\sum\limits_{d|n}d\sum\limits_{i=1}^{n}[\gcd(i,n)=d]\\ \large同除 d 得:\\ \large=\sum\limits_{d|n}d\sum\limits_{i=1}^{\frac{n}{d}}[\gcd(i,\frac{n}{d})=1]\\ =\sum\limits_{d|n}d \varphi(\frac{n}{d}) \]

例题：P1891 疯狂 LCM

\[\sum\limits_{i=1}^{n}lcm(i,n)=n\sum\limits_{i=1}^{n}\frac{i }{\gcd(i,n)} \\ =n\sum\limits_{d|n}\sum\limits_{i=1}^{n}\frac{i}{d\times[gcd(i,n)=d]}\\ =n\sum\limits_{d|n}\sum\limits_{i=1}^{n}\frac{i}{d}[gcd(i,n)=d]\\ =n\sum\limits_{d|n}\sum\limits_{i=1}^{\frac{n}{d}}i[gcd(i,\frac{n}{d})=1]\\ =n\sum\limits_{d|n}\sum\limits_{i=1}^{d}i[gcd(i,\frac{n}{d})=1]\\ \]

又对于 \(\gcd(i,d)=1\) 显然有 \(\gcd(d-i,d)=1\)，所以 \(i\) 成对出现，对于每对之和为 \(d\)，有 \(\frac{\varphi(d)}{2}\) 对。 显然可得 \(\sum_{i=1}^{d}i\times [\gcd(i,d)=1]=\frac{\varphi(d)}{2}d\)。

\[n\sum\limits_{d|n}\sum\limits_{i=1}^{d}i[gcd(i,\frac{n}{d})=1]\\ =n\sum\limits_{d|n}\frac{\varphi(d)}{2}d \]

例题：P2398 GCD SUM

给定 \(n\) ，求 \(\Large\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\gcd(i,j)\)，\(n\le10^5\)。

\[ \large \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} \gcd(i,j)\\ =\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\sum\limits_{d=1}^{n}d[\gcd(i,j)=d]\\ =\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\sum\limits_{d=1}^{n}d[\gcd(\frac{i}{d},\frac{j}{d})=1]\\ =\sum\limits_{d=1}^{n}d\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[\gcd(\frac{i}{d},\frac{j}{d})=1]\\ =\sum\limits_{d=1}^{n}d(\sum\limits_{i=1}^{\frac{n}{d}}2\varphi(i))-1 \]

莫比乌斯反演专题

公式 & 性质

\[\large\large[\gcd(i,j)=1]=\sum\limits_{d|gcd(i,j)}\mu(d)\\ \]

\[\Large\large\sum\limits_{d|n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}\\ \\ \Large\large\sum\limits_{i=1}^{n}\sum\limits_{d|i}\mu(d)=\sum\limits_{d=1}^{n}\lfloor\frac{n}{d}\rfloor\mu(d)\\ \]

套路

\[\Large 对于形如\sum\limits_{i=1}^{n}\sum\limits_{d|i}\mu(d)可以直接枚举d\\ 变为\sum\limits_{d=1}^{n}\sum\limits_{i=1}^{\lfloor \frac{n}{d} \rfloor}\mu(d)=\sum\limits_{d=1}^{n}{\lfloor \frac{n}{d} \rfloor}\mu(d) \]

板子 1

\[\Large\large\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=1]\\ =\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}\sum\limits_{d|gcd(i,j)}\mu(d)\\ =\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}\sum\limits_{d|i}\sum\limits_{d|j}\mu(d)\\ =\sum\limits_{d=1}^{n}\lfloor\frac{n}{d}\rfloor\sum\limits_{j=1}^{m}\lfloor\frac{m}{d}\rfloor\mu(d)\\ =\sum\limits_{d}^{\min(n,m)}\mu(d)×\lfloor\frac{n}{d}\rfloor×\lfloor\frac{m}{d}\rfloor\\ \sum_{i=1}^{n}\sum_{j=1}^{n}[gcd(i,j)=1]=\sum_{d=1}^{n}\mu (d) × \left \lfloor \frac{n}{d} \right \rfloor ^2 \]

板子 2

\[\LARGE\large f(x)=\large\large\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=k]\\ \large\large 当 \gcd(i,j)=k 时 [gcd(i,j)=k]=1 \\ \large\large 这未免有点太啰嗦了，所以离散化一下，变成:\\ \large\large f(x)=\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}[\gcd(i,j)=1]\\ \large\large可得\\ \large\large f(x)=\sum\limits_{d}^{\min(\lfloor\frac{n}{k}\rfloor,\lfloor\frac{m}{k}\rfloor)}\mu(d)×\lfloor\frac{n}{kd}\rfloor×\lfloor\frac{m}{kd}\rfloor \]

板子 3

\[\large\large\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}ij[gcd(i,j)=k]= \large\large\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}ij[gcd(i,j)=1]×k^2\\ \]

\[因为 n 和 m 都为原来的\frac{1}{k}了所以 i, j也为原来的\frac{1}{k}，要把 ij 项补回去所以乘k^2\\ \large\large\sum\limits_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{k}\rfloor}ij\sum\limits_{d|gcd(i,j)}\mu(d)×k^2\\ \sum\limits_{d=1}^{\lfloor\frac{\min(n,m)}{k}\rfloor} \mu(d)×d^2\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{kd}\rfloor}ij×k^2\\ 整理一下\\ k^2×\sum\limits_{d=1}^{\lfloor\frac{\min(n,m)}{k}\rfloor} \mu(d)×d^2\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}i\sum\limits_{j=1}^{\lfloor\frac{m}{kd}\rfloor}j\\ 后两项\sum\limits_{i=1}^{\lfloor\frac{n}{kd}\rfloor}i\sum\limits_{j=1}^{\lfloor\frac{m}{kd}\rfloor}j为等差数列直接求 \]

杜教筛

狄利克雷卷积

设 \(f,g\) 是两个数论函数，它们的狄利克雷卷积卷积是: \(\large\large(f×g)(n)=\sum\limits_{d|n}f(d)g(\frac{n}{d})\)

性质：满足交换律，结合律。

结合狄利克雷卷积得到的几个性质：

\[\mu*I=\epsilon\\ \varphi*I=id\\ \mu*id=\varphi\\ \]

后记

对于符号的解释：

\(\sum\limits_{i=1}^{n}i\) 代表变量 \(i\) 初始值为 \(1\) , \(i\) 的上界为 \(n\) 每次将 \(i+1\) ,并对 \(i\) 求和。

\(d|n\) 代表 \(d\) 是 \(n\) 的约数。

\([a=b]\) 可认为是一个 bool 变量，当 \(a=b\) 时 \([a=b]=1\) 否则 \([a=b]=0\)。

所以 \([a=b]为a==b?1:0\)。

微积分

计算 \(\pi\)

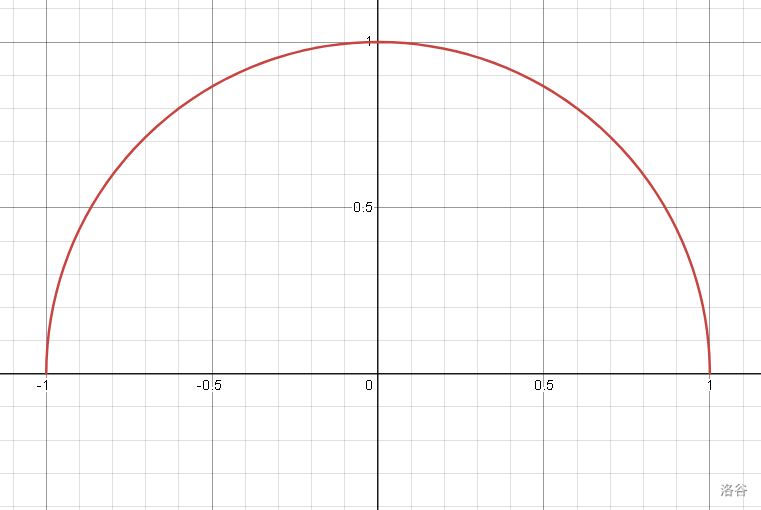
我们知道单位圆的函数为 \(y^2=1-x^2\) ， 而单位圆的面积为 \(\pi\) 我们可以用积分求得单位圆的面积，从而求得 \(\pi\)。

而 \(\int_{a}^{b} f(x)dx\) 代表 \(x\) 从 \(a\) 到 \(b\) 函数 \(f(x)\) 与 \(x\) 轴的面积之和，由于对单位圆积分显然为 \(0\) ，所以需要稍微变形为 \(f(x)=\sqrt{1-x^2}\)。

让我们坐稳了，前方高能！

\[\Large f(x)=\sqrt{1-x^2}\\ \frac{\pi}{4}=\int_{0}^{1}f(x)dx\\ =\lim_{n \to \infty}\sum\limits_{i=1}^{n} f(\frac{i}{n}) \cdot\frac{1}{n}\\ =\lim_{n \to \infty}\sum\limits_{i=1}^{n} \sqrt{1-\frac{i^2}{n^2}} \cdot\frac{1}{n}\\ =\lim_{n \to \infty}\frac{1}{n}\sum\limits_{i=1}^{n} \sqrt{\frac{n^2-i^2}{n^2}} \\ =\lim_{n \to \infty}\frac{1}{n^2}\sum\limits_{i=1}^{n} \sqrt{n^2-i^2} \\ \therefore \frac{\pi}{4}=\lim_{n \to \infty}\frac{1}{n^2}\sum\limits_{i=1}^{n} \sqrt{n^2-i^2} \]