Codeforces难题精选

\(\color{purple}\text{Greedy Change}\)

\(\color{red}\text{Rating:2600}\)
\(\color{green}\text{time:2023.3.9}\)

有时侯越是深入，越难看清，不如置身世外，跟着感觉走。

我们记答案为 \(\text{S}\) 。（即要表示的金额）

其实我们都不难感觉到，大概要找一个接近一种货币 \(T\) 但稍微大一点的值作为 \(\text{S}\)，因为这样贪心的笨蛋用了这种货币 \(T\) 后就只能用更小的货币了，这样就容易造成劣解。但是究竟该怎么找，恐怕难以具象化为程序。

方法是设定一个最下界货币 \(j\) ，上文说了，“笨蛋只能用更小的货币了”，那么正解肯定不会去用很小的货币，设定一个下界 \(j\) ，当表示 \(T\) 时强制只能用 \(j\) 到 \(T\) 之间的货币。 然后对于这种方案润色一下（你暂时不需要明白怎么“润色”），再交给笨蛋做，比较一下答案对不对。

关键变成了枚举这个 \(S\) ，有一点显然， \(S<a[T+1]\) ，（否则笨蛋还会选 \(T\) 么？），不妨先设 \(S=a[T+1]-1\) （\(T\) 枚举），枚举下界 \(j\) ，然后贪心一遍模拟聪明人，此时 \(S\) 可能仍有剩余，方法是简单粗暴地去掉这个剩余；此时又发现可能用的最小货币可能不是 \(j\) ，方法是 \(S+=a[j]\) 。

确定了合法的 \(S\) 后其他就是顺藤摸瓜：模拟笨蛋做一遍，与聪明人对比，如果更劣就更新答案。

嗯，然后就结束了。其实看到这里你肯定还是不明白，没关系，因为我也不明白。冗杂的证明看不来，尚且能根据人类的推理能力得出答案。

其实世界就是这样呢，有时候不需要知道为什么，也会勇敢地尝试。

\(\color{purple}\text{Galaxy Union}\)

\(\color{red}\text{Rating:2700}\)
\(\color{green}\text{time:2023.3.12}\)
简化题面：给定一个 $n $ 点无向基环树，求每个点到其余点最短路之和。

先考虑普通的树怎么做：U285295 的 & 树 。
以一号点为根，怎么求出他到其他点的距离？也许可以树形 \(DP\) ，设置 \(dp[i]\) 表示从 \(i\) 点到其他点的距离， \(sze[i]\) 表示 \(i\) 点子树大小：

void work(int u,int fa){
	sze[u]=1;
	for(int i=head[u];i;i=last[i]){
		int v=to[i];if(v==fa || bk[v]==2)continue;//暂时忽略bk[v]==2
		work(v,u);
		sze[u]+=sze[v];
		dp[u]+=dp[v]+w[i]*sze[v];
	}
	return;
}

然后呢？然后是换根 \(DP\)，求出剩下点为根的答案：

void tree_dp(int u,int fa){
	ans[u]=dp[u];
	for(int i=head[u];i;i=last[i]){
		int v=to[i];if(v==fa || bk[v]==2)continue;//暂时忽略bk[v]==2
		int r1=dp[u],r2=sze[u],r3=dp[v],r4=sze[v];
		dp[u]-=dp[v]+sze[v]*w[i];sze[u]=n-sze[v];
		dp[v]+=dp[u]+sze[u]*w[i];sze[v]=n;
		tree_dp(v,u);
		dp[u]=r1,sze[u]=r2;
		dp[v]=r3,sze[v]=r4;//还原
	}
	return;
}

完成这些后即可通过弱化版的此题。
接下来考虑基环树上：

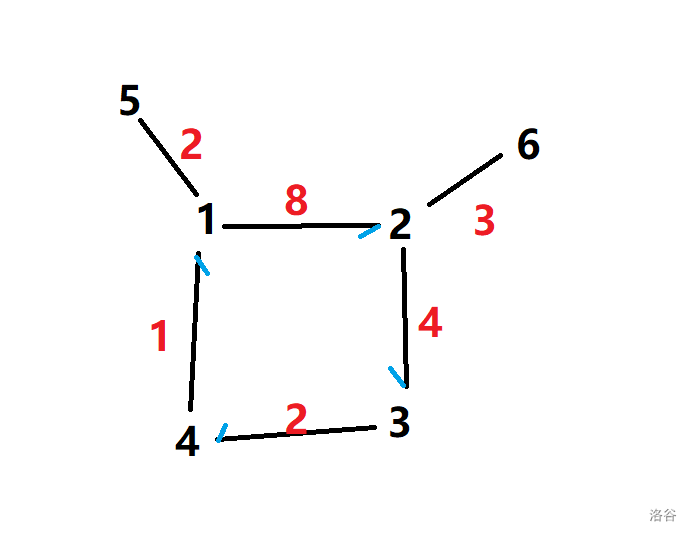
首先找环，这里不多说了。
然后对环上每个点向它的子树做一次树形 \(DP\) 。

接下来考虑以 \(1\) 为起点，那么它的最短路怎么走：发现最优秀走法是对于环上的 \(\text{4,3}\) 点及其子树走逆时针，对于 \(2\) 及其子树走顺时针。子树中的点已经树形 \(DP\) 计算过了，剩下的只要考虑环上的边的贡献即可。

显然有一个性质，对于点 \(i\) 出发 ,有半个环的最优走法是顺时针，剩下半个环是逆时针。我们考虑变换起点时维护环上的走顺时针的点的区间，然后即可计算出环上每个点的答案，最后在对环上每个点的子树内做一次换根\(DP\) 那么这题就结束了。

\(\color{purple}\text{Pairs}\)

\(\color{red}\text{Rating:2700}\)
\(\color{green}\text{time:2023.3.14}\)
简化题面：给定基环树（森林），每个点被染为白或黑色，求基环树的最大匹配，且此时黑色与白色的匹配数量最大。

还是先考虑树上怎么做，考虑树形 \(DP\) ，根据经验，我们可以把最大匹配的权值乘上 \(2e5\) ，显然这样保证优先最多匹配。设置 \(f[i][0]\) 表示 \(i\) 不被匹配时 \(i\) 及其子树最大匹配数， \(f[i][1]\) 表示 \(i\) 不论匹配与否时 \(i\) 及其子树最大匹配数。易得：

\(f[i][0]=\sum_{j∈son[i]}f[j][1]\)
\(f[i][1]=\max(f[i][0],max_{j=son[i]}(f[i][0]-f[j][1]+f[j][0]+2e5+(gender[i]!=gender[j])))\)

然后考虑基环树，显然我们可以删掉一条边变成一棵树，然后枚举这条边选不选，即可得到答案（其实我不是这么写的，但思路大致相同）。

最后提一些细节，如果出现基环树变树的情况，请一定要去重边；以及我 \(bk\) 的时候用 \(bk[u]=fa\) ，但是没想到根的 \(fa=0\) ，白标记了。

\(\color{purple}\text{Help Shrek and Donkey}\)

\(\color{red}\text{Rating:2700}\)
\(\color{green}\text{time:2023.3.15}\)
且不说怎么推概率，欺骗策略真的很好玩。

这里主要写一下纳什均衡。

任何一位玩家在此策略组合下单方面改变自己的策略（其他玩家策略不变）都不会提高自身的收益。

例如这题，（图片来自题解）

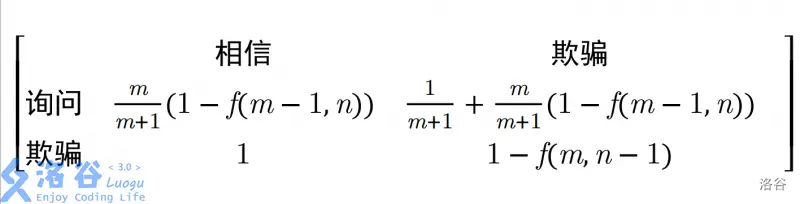
显然，当我们确定先手 \(p\) 的概率询问时（ \(1-p\) 的概率欺骗），后手可以选择相信或不相信，并可能因此改变我们的获胜概率，而此时最优方案就是达到纳什均衡。即后手相不相信，我们获胜的概率都是一样的。

\(p\times P(Ask\&Trust)+(1-p)\times (Fake\&Trust)=p\times P(Ask\&Doubt)+(1-p)\times (Fake\&Doubt)\)

\(\color{purple}\text{P2081 [NOI2012] 迷失游乐园}\)

\(\color{red}\text{Rating:Black}\)
\(\color{green}\text{time:2023.3.30}\)
第一道秒的黑。

如果是一棵树的话，这道题就是一个简单树上 \(DP\) 。然后换根 \(DP\) 。

但是它是一棵基环树，我们发现环上的结点很小，可以暴力对于每个点跑一遍环求出环上起点出发时的答案，然后就又是换根。

细节比较多。

Code

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+110;
int read(){
	int x=0,f=1;char c=getchar();
	while(c>'9' || c<'0'){if(c=='-')f=-1;c=getchar();}
	while(c>='0' && c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return x*f;
} 
int tot,head[N],last[N],to[N],w[N],ODE[N];
void add(int u,int v,int t){to[++tot]=v,w[tot]=t,last[tot]=head[u],head[u]=tot;return;}
int n,m;
double dp[N],ans[N];//dp为向子树走的期望路径 
int bk[N],from[N],fedge[N],FoundCircle;vector<int>Circle,Cedge;
void FindCircle(int u){
	if(FoundCircle)return;
	for(int i=head[u];i;i=last[i]){
		int v=to[i];if(v==from[u])continue;if(FoundCircle)return;
		if(bk[v]){
			int pos=u;
			while(pos!=v){
				bk[pos]=2;
				Circle.push_back(pos);	
				Cedge.push_back(fedge[pos]);
				pos=from[pos];
			}
			bk[v]=2;
			Circle.push_back(v);
			Cedge.push_back(w[i]);
			FoundCircle=1;return;
		}
		else{
			bk[v]=1,from[v]=u,fedge[v]=w[i];
			FindCircle(v);
		}
	}
	return;
}
void TreeDp(int u,int fa){
	for(int i=head[u];i;i=last[i]){
		int v=to[i];if(v==fa || bk[v]==2)continue;
		TreeDp(v,u);
		dp[u]+=(dp[v]+w[i])*(1.0/(ODE[u]-1-(bk[u]==2)+(fa==-2)));
	}
	return;
}
double CircleWalk(int u,int End,int Dire){
//	cout<<u<<" "<<End<<" "<<Dire<<endl;
	if(Dire==1){
		int v=(u+1)%Circle.size();
		int t1=Circle[u];
		if(v==End)return dp[t1];
		else return dp[t1]*(ODE[t1]-2)/(ODE[t1]-1)+(CircleWalk(v,End,Dire)+Cedge[u])/(ODE[t1]-1);
	}
	else{
		int v=(u+Circle.size()-1)%Circle.size();
		int t1=Circle[u];
		if(v==End)return dp[t1];
		else return dp[t1]*(ODE[t1]-2)/(ODE[t1]-1)+(CircleWalk(v,End,Dire)+Cedge[v])/(ODE[t1]-1);
	}
}
void ChangeRoot(int u,int fa){
	ans[u]=dp[u];
//	if(u==2){
//		for(int i=1;i<=n;i++)cout<<dp[i]<<" ";cout<<endl;
//	}
	for(int i=head[u];i;i=last[i]){
		int v=to[i];if(bk[v]==2 || v==fa)continue;
		double RcdDpu=dp[u],RcdDpv=dp[v];
		dp[u]-=(dp[v]+w[i])/ODE[u];
		if(ODE[u]-1!=0)dp[u]=dp[u]*ODE[u]/(ODE[u]-1);
		else dp[u]=0;
		
		dp[v]=dp[v]*(ODE[v]-1)/ODE[v];
		dp[v]+=(dp[u]+w[i])/ODE[v];
		
		ChangeRoot(v,u);dp[u]=RcdDpu,dp[v]=RcdDpv;
	}
	return;
}
void HardWork(){
	bk[1]=1,from[1]=-1;
	FindCircle(1);
//	for(int i=0;i<(int)Circle.size();i++)cout<<Circle[i]<<" ";cout<<endl;
//	for(int i=0;i<(int)Circle.size();i++)cout<<Cedge[i]<<" ";cout<<endl;
	for(int i=0;i<(int)Circle.size();i++)TreeDp(Circle[i],-1);
	for(int i=0;i<(int)Circle.size();i++){
		int u=Circle[i];
		ans[u]+=dp[u]*(ODE[u]-2)/ODE[u];
		ans[u]+=(CircleWalk((i+1)%Circle.size(),i,1)+Cedge[i])/ODE[u];
		ans[u]+=(CircleWalk((i+Circle.size()-1)%Circle.size(),i,-1)+Cedge[(i+Circle.size()-1)%Circle.size()])/ODE[u];
	}
	for(int i=0;i<(int)Circle.size();i++){
		int u=Circle[i];
		dp[u]=ans[u];
		ChangeRoot(u,-1);
	}
	return;
}
void EasyWork(){
	TreeDp(1,-2);
	ChangeRoot(1,-1);
	return;
}
int main(){
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),t=read();
		add(u,v,t),add(v,u,t);ODE[u]++;ODE[v]++;
	}
	if(m==n-1)EasyWork();
	else HardWork();
	double RealAns=0;
	for(int i=1;i<=n;i++)RealAns+=ans[i]/n;
	printf("%.5lf\n",RealAns);
	return 0;
} 
/*
5 5
1 2 1
2 3 2 
3 1 3
3 4 4
4 5 4
*/