[浅谈] 区间相连——线段树优化建边

\(\color{purple}\text{P6348 [PA2011]Journeys}\)

\(\color{green}\text{2023.1.10 10:58}\)
线段树优化建边。
题意：给定一个图，每次对区间 \([a,b]\) 至区间 \([c,d]\) 建边。如果你很蠢，之间暴力建边，那么边复杂度是 \(O(n^2)\) ；如果你聪明一点，对每种边新建两个端点，那么 \([a,b]\) 连起点，\([c,d]\) 连终点，复杂度为 \(O(n)\) ；如果你想通过这道题，那就要用到线段树建边，假设每个点都已经连向某个区间了，那么你只要对区间建边即可。套用线段树，复杂度 \(O(\text{log n})\) 。

具体实现：

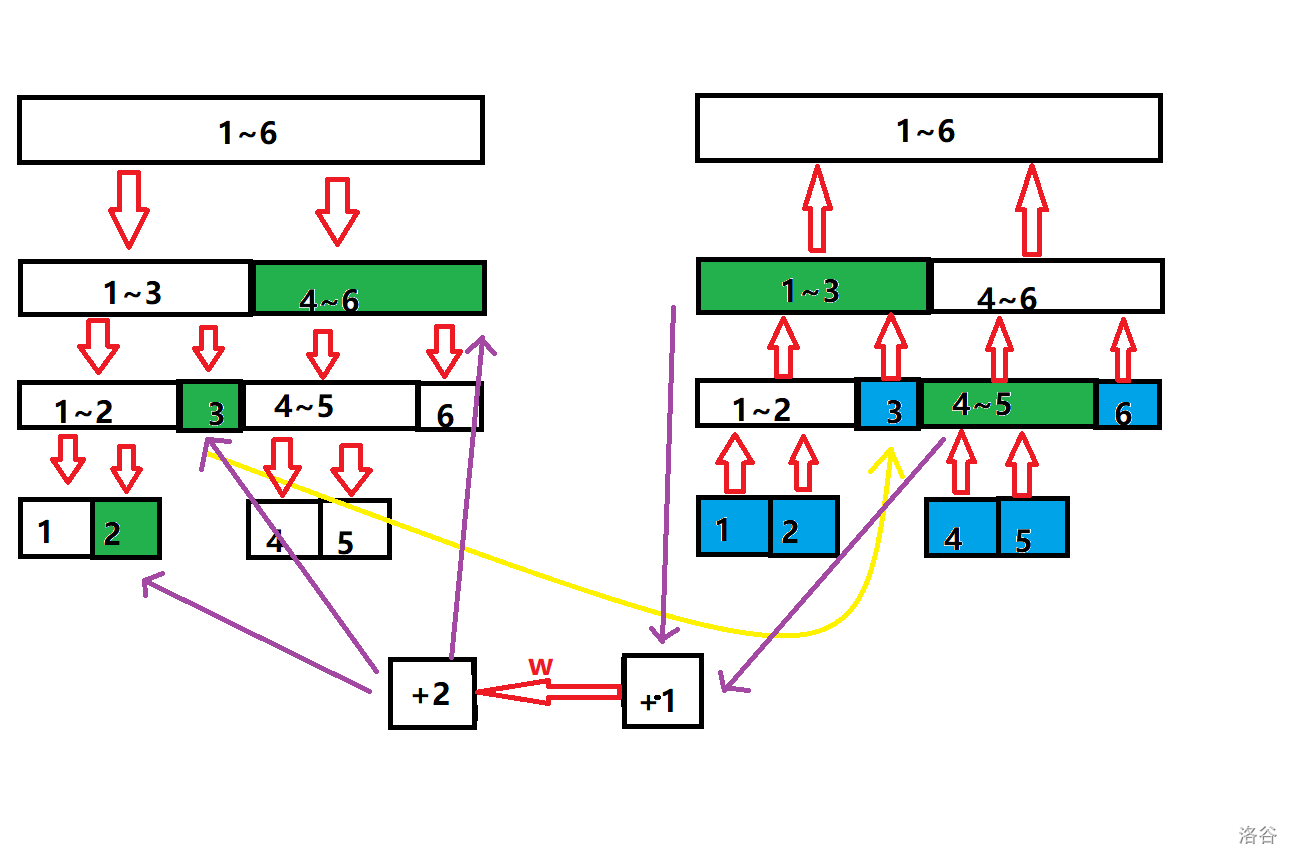
在这个例子中，给定 \(6\) 个点，对 \([1,5]\) 到 \([2,6]\) 建单向边。

真实的点是图中的蓝色点，而真实的边是图中的 \(w\) 边。（其他都是辅助点和边）

如图右边构成了一棵“入树”，其中的每个区间，是对应真实点可以到达的，
如图左边构成了一棵“出树”，其中的每个区间，能到达对应真实点。
（出树的叶子节点连向对应的真实点，即图中的黄边）（图中只标出了“3号点”的黄边，其他省略）。

建边：
首先新建这条边的两端点。（“+1点”和“+2点”）。
然后把入树上的 \([1,5]\) 连向“+1”。
然后把“+2”连向出树上的 \([2,6]\) 。
然后恭喜你学会了“\(\color{red}\text{线段树优化建边}\)”。

---

建完图后，发现真实边权为 \(1\) ，辅助边权为 \(0\) 。那么使用 \(\color{red}\text{01bfs}\) 求最短路最佳。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1.5e7+110,M=1.5e7+10;
int read(){
	int x=0,f=1;char c=getchar();
	while(c>'9' || c<'0'){if(c=='-')f=-1;c=getchar();}
	while(c>='0' && c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return x*f;
}
bool alarm1;
int head[N],to[M],last[M],tot;bool w[M];
void add(int u,int v,int t){to[++tot]=v,w[tot]=t,last[tot]=head[u],head[u]=tot;return;}
int cnt,n,m,p;
int rt1,rt2,ls[N],rs[N];
int pos[N],dis[N];
void build(int &A,int &B,int l,int r){//A是入树，B是出树。 
	if(!A || !B){A=++cnt;B=++cnt;}
	if(l==r){
		pos[l]=A;
		add(B,A,0);
		return;
	}
	int mid=(l+r)>>1;
	build(ls[A],ls[B],l,mid);add(ls[A],A,0),add(B,ls[B],0);
	build(rs[A],rs[B],mid+1,r);add(rs[A],A,0),add(B,rs[B],0);
	return;
}
int U,V;
void Opt(int u,int l,int r,int lim_L,int lim_R){
	if(lim_L<=l && r<=lim_R){
		add(u,U,0);
		return;
	}
	int mid=(l+r)>>1;
	if(lim_L<=mid)Opt(ls[u],l,mid,lim_L,lim_R);
	if(lim_R>mid)Opt(rs[u],mid+1,r,lim_L,lim_R);
	return;
}//入树--边 
void Fpt(int u,int l,int r,int lim_L,int lim_R){
	if(lim_L<=l && r<=lim_R){
		add(V,u,0);
		return;
	}
	int mid=(l+r)>>1;
	if(lim_L<=mid)Fpt(ls[u],l,mid,lim_L,lim_R);
	if(lim_R>mid)Fpt(rs[u],mid+1,r,lim_L,lim_R);
	return;
}//边--出树 
void LingYibfs(){
	memset(dis,0x3f,sizeof(dis));
	deque<int>q;dis[pos[p]]=0;q.push_front(pos[p]);
	while(!q.empty()){
		int u=q.front();q.pop_front();
		for(int i=head[u];i;i=last[i]){
			int v=to[i];
			if(dis[v]>dis[u]+w[i]){
				dis[v]=dis[u]+w[i];
				if(w[i])q.push_back(v);
				else q.push_front(v);
			}
		}
	}
	return;
}
bool alarm2;
int main(){
// 	printf("%.3lf",abs(&alarm1-&alarm2)/1024.0/1024.0);
	n=read(),m=read(),p=read();
	build(rt1,rt2,1,n);
	for(int i=1;i<=m;i++){
		int a=read(),b=read(),c=read(),d=read();
		U=++cnt;V=++cnt;
		add(U,V,1);
		Opt(rt1,1,n,a,b);
		Fpt(rt2,1,n,c,d);
		U=++cnt;V=++cnt;
		add(U,V,1);
		Opt(rt1,1,n,c,d);
		Fpt(rt2,1,n,a,b);
	}
	LingYibfs();
	for(int i=1;i<=n;i++)printf("%d\n",dis[pos[i]]);
	return 0;
}