AtCorder比赛笔记

\(\color{orange}\text{ARC-158}\)

\(\color{RED}\text{Performance:1703}\)
\(\color{GREEN}\text{time:2023.3.12}\)
比赛状态：切了 \(\text{A,B}\) ，两发罚时。（写 \(\text{B}\) 时忘删调试，复制粘贴导致变量名写错）。\(\text{C}\) 题调了 \(50\) 分钟结果因为离散化写错 \(\text{TLE}\) 。

\(\color{purple}\text{A - +3 +5 +7}\)

\(\color{RED}\text{Difficulty:720}\)
题意：
给定三个整数，每次操作可以对三个数分别 \(+3\) ，\(+5\) ， \(+7\) ，求最少多少次操作后三个数相同。不可能输出 "\(-1\)" 。

Solution：我们考虑对三个数排序，操作等价于对两个数分别 \(-2\) ，\(+2\) ，每次对最大最小值分别 \(+2\) ，\(-2\)，直到两个数相同，接下来每三次操作一循环，例如：“\(3,3,9\)”，操作为“ \(+2,+2,-2\) ”如此让数值逼近至相同。

\(\color{purple}\text{B - Sum-Product Ratio}\)

\(\color{RED}\text{Difficulty:1446}\)
题意：给定 \(n\) 个非零数，求 \(\frac{x_i+x_j+x_k}{x_ix_jx_k}\) 的最大与最小值，其中三个数编号互不相同。

Solution：反正这类题就是最大最小正数，最大最小负数，然后乱搞，我们可以无脑一点，直接找到这四类数每类三个，然后暴力枚举。

\(\color{purple}\text{C - All Pair Digit Sums}\)

\(\color{RED}\text{Difficulty:1875}\)
题意：给定 \(n\) 个整数，设 \(f(x)\) 为 \(\text{x}\) 各位数字的和。
求 \(\sum_{i=1}^{n}\sum_{j=1}^{n}f(a[i]+a[j])\) 。\(n\le 2e5\)
。

Solution：显然两个数相加，\(f(a[i]+a[i])=f(a[i])+f(a[j])-9\times g(a[i],a[j])\) ，\(g(a[i],a[j])\) 表示两数相加各位数的进位次数之和。所以我们只需要求出有多少次进位。考虑从个位，十位，百位依次想上考虑，对于 \(a[i]\) ，对他能在千位进位的数只要满足 \(a[j]\%1000>=1000-a[i]\%1000\)（千位时为 \(1000\) ，其他依次类推），就可以了，考虑用树状数组离散化后求解。复杂度 \(O(15n\log n)\)。

alarming：至于我为什么调了 \(50\) 分钟，赛后发现离散话写错，导致某些时候离散化从零开始赋值，树状数组碰到 \(0\) 直接就死循环了。可叹。

\(\color{orange}\text{ARC-157}\) ★

\(\color{RED}\text{Performance:1067}\)
\(\color{GREEN}\text{time:2023.3.16}\)
打的很差，先是把 \(B\) 题目看错，然后又调不出来，耗时 \(\text{1.5 h}\) 也没做出来。

\(\color{purple}\text{A - XXYYX}\)

\(\color{RED}\text{Difficulty:348}\)
题意：求是否存在一个字符串，由 \(X\) 和 \(Y\) 组成，长度为 \(N\) ，且字符串中有 \(A\) 个子串为 \(XX\) ，有 \(B\) 个子串为 \(XY\) ，有 \(C\) 个子串为 \(YX\) ，有 \(D\) 个子串为 \(YX\) ，且 \(A+B+C+D=n-1\) 。

Solution：显然是把 \(ABCD\) 拼接起来。那么如果一个点能接上下一个点就建边。

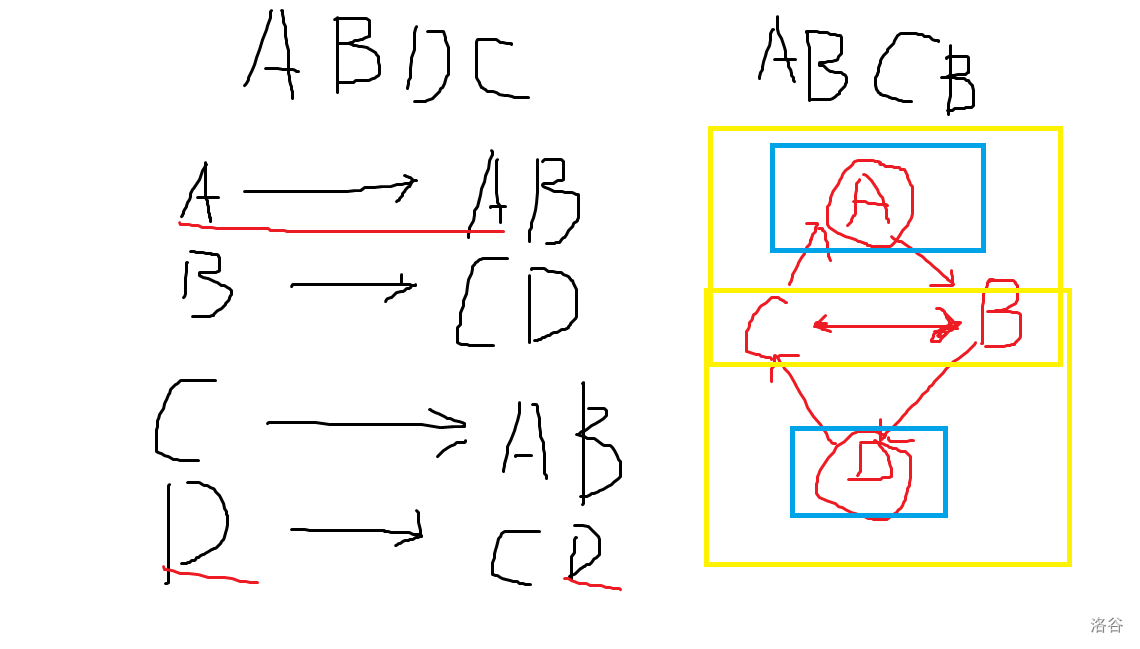
可见 \(ABCD\) 形成了一个大环，可以同时消耗。

int _4=min(min(A,B),min(C,D));
A-=_4,B-=_4,C-=_4,D-=_4;

然后剩下的三个点（或两个）特判一下。因为 \(AD\) 有自环，如果有一个 \(B\) 或 \(C\) 他们一定能消耗掉。而 \(BC\) 则只能一比一消除。所以：

if(A && D && !C && !B){
	printf("No\n");
	return 0;
}
if(abs(B-C)<=1)printf("Yes\n");
else printf("No\n");

\(\color{purple}\text{B - XYYYX}\)

\(\color{RED}\text{Difficulty:1529}\)
其实答案就是 \(y\) 的总数减去 \(y\) 的段数，但是某人代码能力太差。
受不了。

1. 忘记break。
2. 忘记排序。
3. 忘记特判没有 \(y\) 的情况。

\(\color{purple}\text{C - YY Square}\)

\(\color{RED}\text{Difficulty:1802}\)
如果求的是权值和，那么这题很好做，直接 \(DP\) ，可惜求的是平方和。我们意识到 \(f[i-1][j]=a1^2+a2^2+a3^2\) ，假设到这个点时权值加一，实际加的是 \((a1+1)^2+(a2+1)^2+(a3+1)^2\) ,也就等于 \((a1^2+a2^2+a3^2)+2\times (a1+a2+a3)+3\)，然后这道常规题就结束了，同时维护权值与权值的平方即可。

\(\color{orange}\text{ARC-156}\)★

\(\color{RED}\text{Performance:1425}\)
\(\color{GREEN}\text{time:2023.3.16}\)

\(\color{purple}\text{A - Non-Adjacent Flip}\)

\(\color{RED}\text{Difficulty:510}\)

\(\color{purple}\text{B - Mex on Blackboard}\)

\(\color{RED}\text{Difficulty:1415}\)
首先，每次写在黑板上的数只能是 \([0,mex]\) ，\(mex\) 是目前现在的数的 \(mex\) ，显然，当写的数为 \([0,mex-1]\) 时，\(mex\) 不变，写 \(mex\) 时，下次 \(mex\) 会发生改变。

设第 \(i\) 个 \(mex\) 为 \(G[i]\) 。（这个可以预处理）我们枚举黑板上的数最大不超过是第 \(i+1\) 个 \(mex\) ，但大于等于第 \(i\) 个 \(mex\) ,那么必须先放下第 \(i\) 个数，分别为第 \(1->i\) 个 \(mex\) ，所以剩下方案就是 \(k-i\) 个空，每个空取值为 \([0,G[i+1]-1]\)，这个可以用组合数求（我脑瓜有点问题这一步卡了半天），用插板法，每个取值对应一个区间，但是有时候一个值可以每人选，即区间为空，这样不好弄，所以我们自费给每个区间多一个空，然后保证每个区间至少一个空，答案就是 \(C^{G[i+1]-1}_{k-i+G[i+1]-1}\) 。

\(\color{purple}\text{C - Tree and LCS}\)

\(\color{RED}\text{Difficulty:2155}\)
简化题意 ：给定一棵树，对每个点赋予一个 \([1,n]\) 的值，且每个点的值都不同，求所有树上路径值的序列与编号序列 \(\text{LCS}\) 的最大值的最小值的构造方案。

Solution：首先这个最小值可以到 \(1\) 。我们考虑下图这种情况：

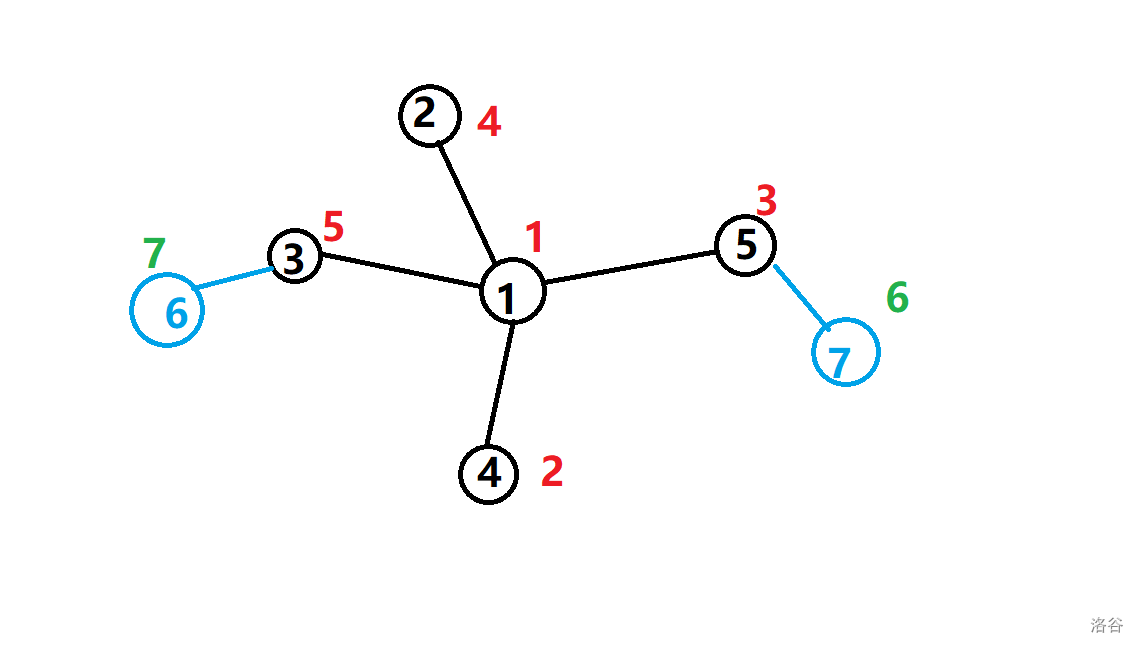
假设我们手摸出了一棵 \(5\) 个节点的树，圆外的是节点的值，圆内是编号，当我们加入新的节点 \(6\) ， \(7\) 时，显然只要交换两者的值就可以把答案维护在 \(1\) ，利用这种思路，我们可以考虑如何构造：
每次取出树中两个入度为 \(0\) 的节点，让他们分别以对方的编号为值，这题就解决了。

\(\color{orange}\text{YZOI-20230319}\)

\(\color{red}\text{Performance:157/300/400 (实际分数/期望分数/满分)}\)
\(\color{GREEN}\text{time:2023.3.19}\)

\(\color{purple}\text{A-weights}\)

\(\color{RED}\text{Difficulty:}\) ★★★

\(\color{lightblue}\text{Solution 1}\)

推推推，假设我们选择数的集合是 \(\text{A}\) ，那么他们能表示的最小数是 \(\gcd(A_1,A_2...A_n)\) ，如果剩下的数都是 \(\gcd(A_1,A_2...A_n)\) 的倍数，那么他们就是能被表示的。于是我们可以一直选数直到所有数都是 \(\gcd(A_1,A_2...A_n)\) 的倍数，但是选数的顺序是什么呢？退退退，使用模拟退火 确定选数顺序，这题就解决了。

\(\color{lightblue}\text{Solution 2}\)

显然根据人类智慧 ，这个答案不会太大。我们直接暴力搜索每个数选或不选，基本剪枝后就能过。

\(\color{purple}\text{B-data}\)

\(\color{RED}\text{Difficulty:}\) ★★☆
考虑没有原序列，那么这就是个裸的动态开点线段树，复杂度 \(O(1e5\log 1e9)\) 。有原序列的话我们可以用 \(ST\) 表查询原序列的最小值。
没想到原题是远古CF2300

\(\color{purple}\text{C-Galaxy Union}\)

\(\color{RED}\text{Difficulty:}\) ★★★☆
重题，博客以前写过了

\(\color{orange}\text{ABC-294}\)

\(\color{red}\text{Performance:2122}\)
\(\color{GREEN}\text{time:2023.3.19}\)
\(\text{ex}\) 题很难，\(\text{ACer}\) 不大于 \(10\) 。这场主要输在 \(F\) 题，想了半天。 \(B\) 题眼瞎贡献一次罚时。总体还是比较好。

\(\color{purple}\text{E - 2xN Grid}\)

\(\color{RED}\text{Difficulty:792}\)
采用双指针，两列齐头并进，每次只要移动落在后面的指针，考虑移动后超过与不超过两种情况。

\(\color{purple}\text{F - Sugar Water 2}\)

\(\color{RED}\text{Difficulty:1891}\)
我们考虑二分答案 \(C\)，然后求出有多少个组合浓度大于 \(C\) ，让这个数量等于 \(k\) ，那么重点在于求有多少个组合浓度大于 \(C\) 。
\(\frac{100(x_i+x_j)}{x_i+y_i+x_j+y_j}\) ，整理得： \(100x_i-k(x_i+y_i)>=k(x_j+y_j)-100x_j\) 。然后们把这个值在两个数组分别从小到大排序，用双指针即可求解。但是这简单题做了 \(\text{30min}\) ，主要原因是这类题做的少，其实以前做过类似的一道，我还写成博客来着，没有那题得经验这题可能甚至切不出来。