题解集合_#1
题解集合_#1 2023.11.21
积压了很久的题解,懒得改前面的博客了,就新开一篇
Luogu P5633 最小度限制生成树
思路部分
先读题,蛤!
我们要求一棵最小生成树,非常咧简单。
但是这棵树上喃,有一个神秘的点 \(s\),欸,这个点咧度数只能为 \(k\)。
这下就瓜起喽!
仔细想想蛤,如果我们在正常咧最小生成树上,把这个点 \(s\) 连的边给砍掉,得到了啥子?
一个 最小生成树森林,是蛤!
所以喃,我们阔以先求出这个不含 \(s\) 的 最小生成树森林,然后再加一些边上去。
找这个森林十分简单蛤!直接对砍掉 \(s\) 之后每个连通块跑个 \(Kruskal\) 就得行喽。
难咧还是啷个加边,可以想到蛤,首先我们还是要单独记录下与 \(s\) 相连的所有点。
(注意蛤,这个时候就要直接 取最小值去重 了蛤,不然要出问题!)
在找这个森林的时候喃,顺便将当前这棵树中 离 \(s\) 最近的点 与 \(s\) 连起来,加个权值。
那如果这棵树不止一个点和 \(s\) 连通喃?
假设枚举到一个边 \((u, v)\),我们阔以钦定这个离 \(s\) 更近咧连通点叫 \(u\),另一个叫 \(v\) 蛤!
然后这个 \(u\) 按照上面咧方法,可能最后就直接和 \(s\) 连喽。
但是这个 \(v\) 蛤,肯定是不会作为这棵树里头离 \(s\) 最近的点来和 \(s\) 连喽。
但是它在后头还是可能要被连的蛤,所以我们就得把它记录一哈。
我们把所有生成树各自离 \(s\) 最近的点连完,发现 \(s\) 咧度数还是凑不够的嘛,那就要考虑 \(v\) 喽!
记录啥子?
其实就是如果我不连 \((u, v)\) 这个蛤蟆,而是直接连 \((s, v), (s, u)\),我亏了好多?
显然 \((s, u)\) 本身就要连,所以记录咧这个权值实质上就是 \(w(s, v) - w(u, v)\) 蛤!
这时候就有人要说了噻
那要是 \(u\) 这个点到后头没有被连到 \(s\) 上(树里头有比 \(u\) 离 \(s\) 更近的点),那啷个办?
莫得关系蛤!考虑我们每次加边咧时候做了一个 并查集 的合并,并让离 \(s\) 近的点当爸爸
那就是说喃,如果后头有一个更近的点,加入的时候它就会和当前离 \(s\) 最近的点比较
(当前并查集的祖先噻!)
然后如果比这个点离 \(s\) 还要近喽,那就记录这个点,再当它咧爸爸就完事喽
具体来讲:
我们有 \(u, v, k\) 三个满足 \(dis(s, v) > dis(s, u) > dis(s, k)\)
还有 \((s, u), (s, v), (s, k), (u, v), (k, v)\) 五条边边
那我们就会在枚举到 \((u, v)\) 的时候记录 \(v\),让 \(u\) 当爸爸。
然后枚举到 \((k, v)\) 的时候发现喽 \(v\) 的爸爸 \(u\),比较 \(u, k\) 到 \(s\) 咧距离,\(k\) 更近蛤!
所以再记录 \(u\),让 \(k\) 当爸爸就阔以喽!
最后我们就把这森林里头所有树根连上 \(s\)(记住蛤!根一直是树里头离 \(s\) 最近的点!)
如果这个时候 \(s\) 度数都超了 \(k\),那就玩完,根本 \(Impossible\)!
如果这个时候 \(s\) 度数 加上前面记录 的那种 \(v\) 咧个数还凑不够 \(k\) 喃,也玩完喽,\(Impossible\)!
其他情况,我们就要把刚刚记录的那一堆点拿出来,看看那个换上之后亏咧少!
排个序蛤,然后一条一条加上,到度数凑够就行。
实现部分
听上去很复杂喃,但是实现起来相当的快!
先开个结构体记下边,十分好用
struct Edge {
int u, v, w;
inline bool operator < (const Edge &a) const {
return w < a.w;
}
} E[MAXM << 1];
然后打个我们最喜欢咧 并查集板子(啷个合并都行蛤,注意 路径压缩!)
之后先跳到读入处理,我们只直接连端点莫得 \(s\) 的边,其他边 取最小去重。
for (int i = 1; i <= M; ++ i) {
cin >> u >> v >> w;
if (u == S) Val[v] = min(Val[v], w);
else if (v == S) Val[u] = min(Val[u], w);
else Add_Edge(u, v, w);
}
最重点的东西来了蛤!魔改 \(Kruskal\) ,先是找森林的部分!
sort(E + 1, E + tot + 1); // 边权排序!
for (int i = 1; i <= tot; ++ i) {
fu = F(E[i].u), fv = F(E[i].v); // 找爸爸噻!
if (fu == fv) continue; // 在一个家头就跳过
if (Val[fu] > Val[fv]) swap(fu, fv); // 找到离 s 更近的 u
f[fv] = fu, Ans += E[i].w; // 合并!然后直接连上 (u, v)
if (Val[fv] < 1e9) V.push_back(Val[fv] - E[i].w); // 记录远点的 v 蛤!
}
然后加边
int Deg = 0; // 记录度数噻!
for (int i = 1; i <= N; ++ i) {
if (f[i] != i || i == S) continue; // 非生成树根 / 源点 都不是要找的对象蛤!
if (Val[i] > 1e9) exit(!bool(cout << "Impossible" << endl)); // 不连通喽!
++ Deg, Ans += Val[i]; // 直接,连,吧
}
// 判断度数可以凑得到不?
if (Deg > K || Deg + V.size() < K) exit(!bool(cout << "Impossible" << endl));
sort(V.begin(), V.end()); // 按亏得最少咧排序
for (int i = 0; i < K - Deg; ++ i) Ans += V[i]; // 凑齐度数蛤!
return Ans;
就结束喽!
最后放个完整的代码,非常的规范!
完整代码
#include <bits/stdc++.h>
const int MAXN = 50005;
const int MAXM = 500005;
using namespace std;
struct Edge {
int u, v, w;
inline bool operator < (const Edge &a) const {
return w < a.w;
}
} E[MAXM << 1];
int tot;
inline void Add_Edge (int u, int v, int w) {
E[++ tot] = {u, v, w};
}
int f[MAXN], s[MAXN], Val[MAXN];
inline void Init (int N) {
for (int i = 1; i <= N; ++ i) f[i] = i, s[i] = 1;
}
inline int F (int u) {
return u == f[u] ? u : f[u] = F(f[u]);
}
inline void Merge (int u, int v) {
u = F(u), v = F(v);
if (u == v) return;
if (s[u] < s[v]) swap(u, v);
f[v] = u, s[u] += s[v];
}
int N, M, S, K;
inline int Kruskal (int Ans = 0, int Cnt = 0) {
sort(E + 1, E + tot + 1), Init(N);
int fu, fv;
vector <int> V;
for (int i = 1; i <= tot; ++ i) {
fu = F(E[i].u), fv = F(E[i].v);
if (fu == fv) continue;
if (Val[fu] > Val[fv]) swap(fu, fv);
f[fv] = fu, Ans += E[i].w;
if (Val[fv] < 1e9) V.push_back(Val[fv] - E[i].w);
}
int Deg = 0;
for (int i = 1; i <= N; ++ i) {
if (f[i] != i || i == S) continue;
if (Val[i] > 1e9) exit(!bool(cout << "Impossible" << endl));
++ Deg, Ans += Val[i];
}
if (Deg > K || Deg + V.size() < K) exit(!bool(cout << "Impossible" << endl));
sort(V.begin(), V.end());
for (int i = 0; i < K - Deg; ++ i) Ans += V[i];
return Ans;
}
int u, v, w;
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
memset(Val, 63, sizeof Val);
cin >> N >> M >> S >> K;
for (int i = 1; i <= M; ++ i) {
cin >> u >> v >> w;
if (u == S) Val[v] = min(Val[v], w);
else if (v == S) Val[u] = min(Val[u], w);
else Add_Edge(u, v, w);
}
cout << Kruskal() << endl;
return 0;
}
Luogu P2619 [国家集训队] Tree I
思路部分
考虑 \(Kruskal\) 会贪心从小到大去枚举边权
当钦定有解的时候,可以想到给白边都加一定的权值
那么一定可以找到一个 加的权值,使得刚好有 \(need\) 条白边在加完权后的最小生成树中选中
二分加的 权值,最后减去即可
完整代码
#include <bits/stdc++.h>
const int MAXN = 50005;
const int MAXM = 100005;
using namespace std;
int L = -120, R = 120, Mid;
struct Edge {
int u, v, w;
bool c;
inline bool operator < (const Edge &a) const {
return (w + c * Mid == a.w + a.c * Mid) ? c > a.c : w + c * Mid < a.w + a.c * Mid;
}
} E[MAXM << 1];
int tot;
inline void Add_Edge (int u, int v, int w, bool c) {
E[++ tot] = {u, v, w, c};
}
int f[MAXN], s[MAXN];
inline void Init (int N) {
for (int i = 1; i <= N; ++ i) f[i] = i, s[i] = 1;
}
inline int F (int x) {
return x == f[x] ? x : f[x] = F(f[x]);
}
inline void Merge (int x, int y) {
x = F(x), y = F(y);
if (x == y) return;
if (s[x] > s[y]) swap(x, y);
f[x] = y, s[y] += s[x];
}
int N, M, Lim, Now;
inline int Kruskal (int Ans = 0, int Cnt = 0) {
Init(N);
sort(E + 1, E + M + 1);
int u, v;
for (int i = 1; i <= M; ++ i) {
u = F(E[i].u), v = F(E[i].v);
if (u == v) continue;
Now += E[i].c, Merge(u, v), Ans += E[i].w + E[i].c * Mid;
if (++ Cnt == N - 1) return Ans;
}
if (Cnt == N - 1) return Ans;
return -1;
}
int FinalAns = 1e9;
inline bool Check (int T) {
Now = 0;
int Temp = Kruskal();
if (Temp == -1 || Now < Lim) return 0;
else FinalAns = Temp - Lim * T;
return 1;
}
int u, v, w;
bool c;
int main () {
cin >> N >> M >> Lim;
for (int i = 1; i <= M; ++ i) {
cin >> u >> v >> w >> c;
Add_Edge (u + 1, v + 1, w, !c);
}
while (L <= R)
Check((Mid = (L + R) >> 1)) ? L = Mid + 1 : R = Mid - 1;
cout << FinalAns << endl;
return 0;
}
Luogu CF739E Gosha is hunting
思路部分
首先肯定可以 \(O(N^3)\) 简单 \(DP\) 蛤!
直接设 \(f[i][j][k]\) 表示抓了前 \(i\) 个,用 \(j\) 宝贝球,\(k\) 超级球的期望
(宝贝球抓到概率为 \(u[i]\),普通球为 \(p[i]\))
显然
然后可以发现一个神秘的玩意儿
当 \(i, j\) 固定时,\(k\) 与 \(f[i][j][k]\) 成正关系,可以感性理解为用的球越多抓到期望越大。
然后 \(wqs\) 二分,和上一个题比较像蛤,可以给每个球一个权值。
每次用球的时候就减去这个权值,然后就可以假定球无限使用。
二分出权值大小,使得取最大值的时候使用的球数符合条件即可。
从几何意义上讲,原答案就是 一个这样的函数
纵轴是抓到的期望,横轴是使用的个数,我们想找在使用个数不超过限制时的 最大函数值
但是实际上并不存在这个函数,或说 不知道具体的表示,所以需要拟合这个东西
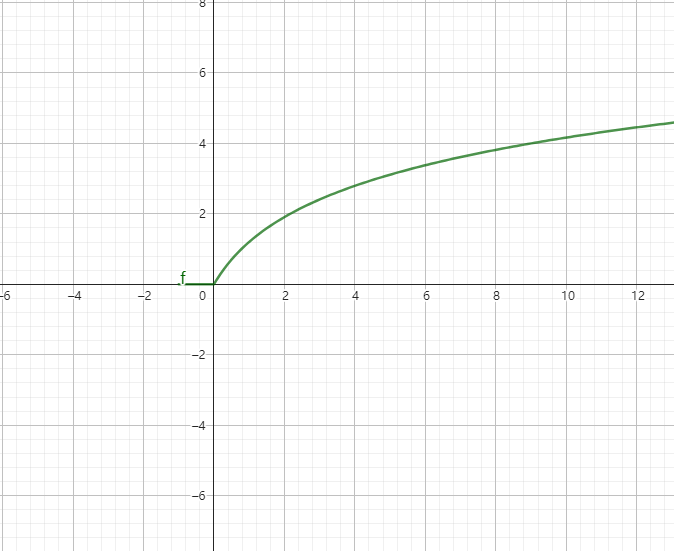
可以想到引 直线与该函数相切
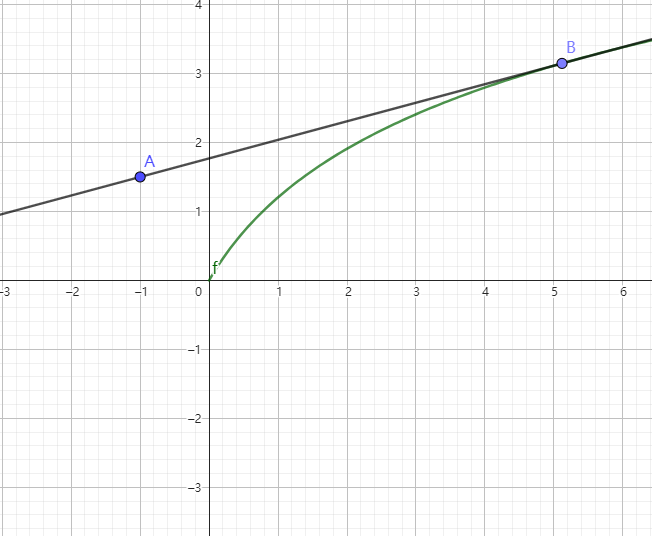
然后发现,直线 斜率,截距 均与 切点横坐标 成正关系
故而可以通过 二分直线截距,对应找到切点(最大值)的横坐标(使用球的个数)
这个就是 给每个球加权 的本质(权值即相当于截距)
将 超级球和宝贝球 放到一起做 两次 \(wqs\) 二分 似乎是错的
感性理解说 两个上凸函数 重合的部分是一个平面,不易直接二分
然后可以将后面一改成 三分 的做法,具体参考 \(Hanghang\) (Link?
但是蛤,这个题直接 两次二分 居然是可以过的!神秘
时间复杂度 \(O(N \log^2 N) \to 62 ms\)
当然,正确性完备的 一次二分 也可以卡过,时间复杂度 \(O(N^2 \log N) \to 717 ms\)
完整代码
\(O(N \log^2 N)\)
#include <bits/stdc++.h>
const int MAXN = 2005;
const double EPS = 1e-8;
using namespace std;
double Dp[MAXN], FA[MAXN], FB[MAXN];
double Ba[MAXN], Sp[MAXN];
long double L1 = 0, R1 = 2, M1, L2 = 0, R2 = 2, M2;
long double Ans, Xpos1, Xpos2;
int N, A, B, XA, XB;
inline void Check (long double k1, long double k2) {
memset (FA, 0, sizeof FA);
memset (FB, 0, sizeof FB);
XA = XB = 0; Ans = 0;
for (int i = 1; i <= N; ++ i) {
Dp[i] = Dp[i - 1], FA[i] = FA[i - 1], FB[i] = FB[i - 1];
if (Dp[i] < Dp[i - 1] + Ba[i] - k1)
Dp[i] = Dp[i - 1] + Ba[i] - k1, FA[i] = FA[i - 1] + 1, FB[i] = FB[i - 1];
if (Dp[i] < Dp[i - 1] + Sp[i] - k2)
Dp[i] = Dp[i - 1] + Sp[i] - k2, FB[i] = FB[i - 1] + 1, FA[i] = FA[i - 1];
if (Dp[i] < Dp[i - 1] + Ba[i] + Sp[i] - Ba[i] * Sp[i] - k1 - k2)
Dp[i] = Dp[i - 1] + Ba[i] + Sp[i] - Ba[i] * Sp[i] - k1 - k2, FA[i] = FA[i - 1] + 1, FB[i] = FB[i - 1] + 1;
if (Dp[i] > Ans) Ans = Dp[i], XA = FA[i], XB = FB[i];
}
return;
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> A >> B;
for (int i = 1; i <= N; ++ i) cin >> Ba[i];
for (int i = 1; i <= N; ++ i) cin >> Sp[i];
while (R1 - L1 > EPS && (M1 = (L1 + R1) / 2.0)) {
L2 = 0, R2 = 2;
while (R2 - L2 > EPS && (M2 = (L2 + R2) / 2.0)) {
Check(M1, M2);
(XB <= B) ? R2 = M2, Xpos2 = M2 : L2 = M2;
}
Check(M1, Xpos2);
(XA <= A) ? R1 = M1, Xpos1 = M1 : L1 = M1;
}
cout << Ans + Xpos1 * A + Xpos2 * B << endl;
return 0;
}
\(O(N^2 \log N)\)
#include <bits/stdc++.h>
const int MAXN = 2005;
const double EPS = 1e-8;
using namespace std;
double Dp[MAXN][MAXN], F[MAXN][MAXN];
double Ba[MAXN], Sp[MAXN];
long double L = 0, R = 2, M;
long double Ans, Xpos;
int N, A, B;
inline bool Check (long double k) {
memset (Dp, 0, sizeof Dp);
memset (F, 0, sizeof F);
int X = 0; Ans = 0;
for (int i = 1; i <= N; ++ i)
for (int j = 0; j <= A && j <= i; ++ j) {
Dp[i][j] = Dp[i - 1][j], F[i][j] = F[i - 1][j];
if (j && Dp[i][j] < Dp[i - 1][j - 1] + Ba[i])
Dp[i][j] = Dp[i - 1][j - 1] + Ba[i], F[i][j] = F[i - 1][j - 1];
if (Dp[i][j] < Dp[i - 1][j] + Sp[i] - k)
Dp[i][j] = Dp[i - 1][j] + Sp[i] - k, F[i][j] = F[i - 1][j] + 1;
if (j && Dp[i][j] < Dp[i - 1][j - 1] + Ba[i] + Sp[i] - Ba[i] * Sp[i] - k)
Dp[i][j] = Dp[i - 1][j - 1] + Ba[i] + Sp[i] - Ba[i] * Sp[i] - k, F[i][j] = F[i - 1][j - 1] + 1;
if (Dp[i][j] > Ans) Ans = Dp[i][j], X = F[i][j];
}
return X <= B;
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> A >> B;
for (int i = 1; i <= N; ++ i) cin >> Ba[i];
for (int i = 1; i <= N; ++ i) cin >> Sp[i];
while (R - L > EPS && (M = (L + R) / 2.0))
Check(M) ? R = M, Xpos = M : L = M;
cout << Ans + Xpos * B << endl;
return 0;
}
Luogu P4948 数列求和
思路部分
颓狮子题,考虑分 \(a =1\) 与否两种情况
需要简单应用 二项式定理
\(a = 1\) 时
\(O(k ^ 2)\) 递推即可
\(a \neq 1\) 时
\(O (k ^ 2)\) 递推即可
完整代码
#include <bits/stdc++.h>
const int MAXK = 2005;
const int MOD = 1000000007;
using namespace std;
long long Mul[MAXK];
long long Final[MAXK];
inline long long qpow (const long long a, const long long b) {
if (b == 1) return a % MOD;
const long long Ret = qpow (a, b >> 1);
if (b & 1) return Ret * Ret % MOD * (a % MOD) % MOD;
else return Ret * Ret % MOD;
}
inline void Init (int N) {
Mul[1] = 1;
for (int i = 2; i <= N; ++ i) Mul[i] = Mul[i - 1] * i % MOD;
}
inline long long C (int x, int y) {
if (x == y + 1|| y == 1) return x;
if (x == y || y == 0) return 1;
return Mul[x] * qpow(Mul[x - y], MOD - 2) % MOD * qpow(Mul[y], MOD - 2) % MOD;
}
long long N, A, K;
long long Ans, Tmp;
int main () {
Init(2000);
cin >> N >> A >> K;
if (A == 1) {
Final[0] = N;
for (int i = 1; i <= K; ++ i) {
Ans = qpow(N + 1, i + 1) - 1, Ans = Ans % MOD;
Tmp = 0;
for (int j = 0; j <= i - 1; ++ j) Tmp += (C(i + 1, j) * Final[j]) % MOD;
Tmp = Tmp % MOD, Ans = (Ans + MOD - Tmp) % MOD;
Ans = Ans * qpow(i + 1, MOD - 2) % MOD;
Final[i] = Ans;
}
} else {
Final[0] = qpow(A, N + 1) - A, Final[0] = (MOD + Final[0] % MOD) % MOD;
Final[0] = Final[0] * qpow(A - 1, MOD - 2) % MOD;
for (int i = 1; i <= K; ++ i) {
Tmp = 0;
for (int j = 0; j <= i - 1; ++ j) Tmp += (C(i, j) * Final[j] % MOD);
Tmp = Tmp % MOD, Tmp = MOD - Tmp, Tmp += (qpow(N + 1, i) * qpow(A, N) % MOD - 1), Tmp = Tmp % MOD;
Tmp = Tmp * (A % MOD) % MOD * qpow(A - 1, MOD - 2) % MOD;
Final[i] = Tmp;
}
}
cout << Final[K] << endl;
return 0;
}
Luogu P6419 [COCI2014-2015#1] Kamp
思路部分
考虑在 一棵树上 要对 每个点 求取答案,可以想到 换根 \(DP\)
思考需要维护什么东西?
我们发现司机在 送完一个人 后是可以 不回原点的
也就是我们应当维护 送完子树内所有人再回到原点 的值 再减去最长链长
所以可以对每个子树维护 根开始的最长链,次长链
换根时 合并更新 即可
实现部分
设 \(T_u\) 为 在以 \(u\) 为根的子树内,将所有人送完并回到 \(u\) 的时间
设 \(S_u\) 为 以 \(u\) 为根的子树内需要送的人数
设 \(fL_u, sL_u\) 为 在以 \(u\) 为根的子树内,从 \(u\) 开始的最长链,次长链长度
第一遍 \(DFS\) 更新子树内信息
void DFS_1 (int x) {
if (Peo[x]) S[x] = 1; // 当前节点有人
Vis[x] = 1; // 标记访问
int v, w;
for (int i = H[x]; i; i = E[i].nxt) {
v = E[i].to, w = E[i].w;
if (Vis[v]) continue; // 访问过
DFS_1 (v); // 先更新子节点子树内的信息
if (S[v]) { // 子树内(包括自己)有人需要送
S[x] += S[v], T[x] += 2 * w + T[v]; // 更新子树内人数,来回距离
if (L[v].f + w >= L[x].f) L[x].s = L[x].f, L[x].f = L[v].f + w, L[x].id = v; // 更新最长链 及 次长链
else if (L[v].f + w > L[x].s) L[x].s = L[v].f + w;
}
}
}
第二遍换根 \(DFS\) ,合并全局最长链,更新最终答案
void DFS_2 (int x) {
int v, w;
Vis[x] = 1;
for (int i = H[x]; i; i = E[i].nxt) {
if (Vis[E[i].to]) continue;
v = E[i].to, w = E[i].w;
// 这里实际上是在更新每个 v 的答案,而不是 x 的答案
// 如果 v 子树内没人要送,那么以 v 为根的答案相当于把 x 子树内所有人送完在加上 x <-> v 往返
if (!S[v]) Dp[v] = Dp[x] + 2 * w, L[v].f = L[x].f + w;
// 如果 v 子树内包含所有人,答案就是前面 T[v],最后减去最长链(输出答案的时候)
else if (!(K - S[v])) Dp[v] = T[v];
else { // 以 x 为根或 v 为根子树内都有人要送,那么答案相等(x <-> v 都会被走到 或 都不被走到)
Dp[v] = Dp[x];
if (L[x].id != v && L[v].f < L[x].f + w)
// 用 x 为根最长链来更新 v 为根最长链,需要保证 x 为根最长链不经过 v,不然可能和 v 本身最长链相同
L[v].s = L[v].f, L[v].f = L[x].f + w, L[v].id = x;
else if (L[v].f < L[x].s + w) // 更新次长链(这里可以经过 v)
L[v].s = L[v].f, L[v].f = L[x].s + w, L[v].id = 1;
// 用 x 为根次长链来更新 v 为根最长链,需要保证 x 为根最长链不经过 v...
else if (L[x].id != v && L[v].s < L[x].f + w)
L[v].s = L[x].f + w;
else if (L[v].s < L[x].s + w) // 更新次长链(这里可以经过 v)
L[v].s = L[x].s + w;
}
DFS_2 (E[i].to); // 向子树递归
}
}
最后输出 \(DP[i] - L[i].f\) 即可
完整代码
#include <bits/stdc++.h>
const int MAXN = 500005;
using namespace std;
struct Edge {
int to, nxt, w;
} E[MAXN << 1];
struct Line {
long long f, s, id;
} L[MAXN];
int H[MAXN], tot;
bool Peo[MAXN];
inline void Add_Edge (int u, int v, int w) {
E[++ tot] = {v, H[u], w}, H[u] = tot;
E[++ tot] = {u, H[v], w}, H[v] = tot;
}
bool Vis[MAXN];
long long S[MAXN], T[MAXN], Dp[MAXN];
void DFS_1 (int x) {
if (Peo[x]) S[x] = 1;
Vis[x] = 1;
int v, w;
for (int i = H[x]; i; i = E[i].nxt) {
v = E[i].to, w = E[i].w;
if (Vis[v]) continue;
DFS_1 (v);
if (S[v]) {
S[x] += S[v], T[x] += 2 * w + T[v];
if (L[v].f + w >= L[x].f) L[x].s = L[x].f, L[x].f = L[v].f + w, L[x].id = v;
else if (L[v].f + w > L[x].s) L[x].s = L[v].f + w;
}
}
}
int N, K;
void DFS_2 (int x) {
int v, w;
Vis[x] = 1;
for (int i = H[x]; i; i = E[i].nxt) {
if (Vis[E[i].to]) continue;
v = E[i].to, w = E[i].w;
if (!S[v]) Dp[v] = Dp[x] + 2 * w, L[v].f = L[x].f + w;
else if (!(K - S[v])) Dp[v] = T[v];
else {
Dp[v] = Dp[x];
if (L[x].id != v && L[v].f < L[x].f + w)
L[v].s = L[v].f, L[v].f = L[x].f + w, L[v].id = x;
else if (L[v].f < L[x].s + w)
L[v].s = L[v].f, L[v].f = L[x].s + w, L[v].id = 1;
else if (L[x].id != v && L[v].s < L[x].f + w)
L[v].s = L[x].f + w;
else if (L[v].s < L[x].s + w)
L[v].s = L[x].s + w;
}
DFS_2 (E[i].to);
}
}
int u, v, w, p;
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> K;
for (int i = 1; i < N; ++ i)
cin >> u >> v >> w, Add_Edge(u, v, w);
for (int i = 1; i <= K; ++ i)
cin >> p, Peo[p] = 1;
DFS_1 (1), Dp[1] = T[1];
memset (Vis, 0, sizeof Vis);
DFS_2 (1);
for (int i = 1; i <= N; ++ i) cout << Dp[i] - L[i].f << endl;
return 0;
}
Luogu P2607 [ZJOI2008] 骑士
Luogu P1352 没有上司的舞会 的基环树版,十分好!
思路部分
回顾一下 上面这一道,实质上就是 树形 \(DP\) 的板子
简要题意
每个人有一个 直接上司 和 快乐值
一个人能来舞会 当且仅当他的直接上司没来
每个来了的人会贡献他的 快乐值,求 快乐值的和最大
(区别在于存在一个 最高上司,不会成环)
设 \(DP[i][j]\) 是第 \(i\) 个人 是否参加舞会 所得的最大快乐值
将每个人和自己上司连边
若有边 \((u, v)\),\(u\) 是 \(v\) 的上司,显然有方程
找到 最高上司 \(R\) 后向下 \(DP\) 即可,最后输出 \(\max(DP[R][0], DP[R][1])\)
回到这个题
我们发现其实就是树上 多了一条边 蛤!这样形成了一个 基环树(会有一个环)
注意,这个题不保证连通,所以实质上是一个 基环树森林,对每个基环树分别解决即可
环这个东西看着 十分恶心,所以我们 不要环!把它拆开
显然,将 环上任意一边 \((u, v)\) 去掉,我们就又得到了 一棵树,钦定 \(u\) 为根
可以跑上面的东西,但是由于此时的 ”最高上司 \(u\) “ 实质上是与某个 **叶子 \(v\) ** 连边的
两者只能选一个
所以我们钦定 ”最高上司 \(u\)“ 不参加,然后再让 \(v\) 成为 "最高上司" 跑一遍(此时 \(v\) 不参加)
答案即是 \(\max (DP[u][0], DP[v][0])\)
注意是 基环树森林 蛤!最终答案是 所有树统计出的答案之和
实现部分
链式前向星存边,由于这是有 环 的,环上任意一点 一直往儿子走就可以找到环
所以只需要建 单向边
struct Edge {
int to, nxt;
}E[MAXN];
int H[MAXN], tot, N;
inline void Add_Edge (int u, int v) {
E[++ tot] = {v, H[u]}, H[u] = tot;
}
找环,并断边,两端点分别跑一遍
inline void Find_Cir (int S) {
int R = S;
while (!Vis[S]) Vis[S] = 1, R = S, S = F[S];
DFS(R, R), Tmp1 = Dp[R][0];
DFS(S, S), Tmp2 = Dp[S][0];
Ans += max(Tmp1, Tmp2);
}
典
inline void DFS (int S, int R) {
Vis[S] = 1, Dp[S][0] = 0, Dp[S][1] = Hp[S];
for (int i = H[S]; i; i = E[i].nxt) {
if (E[i].to != R) {
DFS(E[i].to, R);
Dp[S][0] += max(Dp[E[i].to][0], Dp[E[i].to][1]);
Dp[S][1] += Dp[E[i].to][0];
}
}
}
整个实现非常的少蛤,没有狠压都只有 \(1000B\)
完整代码
#include <bits/stdc++.h>
const int MAXN = 1000005;
using namespace std;
struct Edge {
int to, nxt;
}E[MAXN];
int H[MAXN], tot, N;
inline void Add_Edge (int u, int v) {
E[++ tot] = {v, H[u]}, H[u] = tot;
}
bool Vis[MAXN];
int Hp[MAXN], F[MAXN];
long long Dp[MAXN][2], Ans, Tmp1, Tmp2;
inline void DFS (int S, int R) {
Vis[S] = 1, Dp[S][0] = 0, Dp[S][1] = Hp[S];
for (int i = H[S]; i; i = E[i].nxt) {
if (E[i].to != R) {
DFS(E[i].to, R);
Dp[S][0] += max(Dp[E[i].to][0], Dp[E[i].to][1]);
Dp[S][1] += Dp[E[i].to][0];
}
}
}
inline void Find_Cir (int S) {
int R = S;
while (!Vis[S]) Vis[S] = 1, R = S, S = F[S];
DFS(R, R), Tmp1 = Dp[R][0];
DFS(S, S), Tmp2 = Dp[S][0];
Ans += max(Tmp1, Tmp2);
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N;
for (int i = 1; i <= N; ++ i)
cin >> Hp[i] >> F[i], Add_Edge(F[i], i);
for (int i = 1; i <= N; ++ i)
if (!Vis[i]) Find_Cir(i);
cout << Ans << endl;
return 0;
}
Luogu P4381 [IOI2008] Island
思路部分
这个 IOI 的题啊出的是相当的不规范,差点就让我没读懂题,瓜起!
其实注意渡船当且仅当 两个岛不连通 时才能使用就行
然后就是对每个 基环树求直径 就行
先对环上的每一个点求出其子树内的 最长次长链,顺带就可以求出每个点子树内的 直径
在环上任意断边,维护一个 前缀长度和 + 子树内最长链 的最大值,就是下面这个
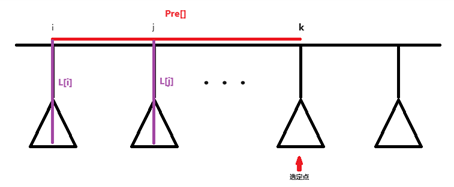
(图中 \(DP[k] = \max(Pre[k - i] + L[i], Pre[k - j] + L[j], Pre[k - ...] + L[...])\))
显然,当图中 \(k\) 指针向右移动时,所选择的 左端最长链 位置也 单调向右
所以在这个链上可以 \(O(N)\) 处理出 经过该链 的 最大直径(\(\max(DP[k] + L[k])\))
回到环考虑,无非是任选两点时 有两条路径
故而同上再处理一下 后缀时的情况 两种取 \(\max\) 即可
完整代码
#include <bits/stdc++.h>
const int MAXN = 1000005;
using namespace std;
bool Vis[MAXN];
int In[MAXN], Out[MAXN];
int To[MAXN], W[MAXN];
long long G[MAXN], F[MAXN];
int N;
long long Ans;
int Q[MAXN], H = 0, T;
inline long long GetV (int x) {
-- Out[x];
long long Ret1 = G[x], Ret2 = -1e9, Tmp1 = F[x], Tmp2 = F[x], Sum = W[x];
x = To[x];
while (Out[x]) {
Ret1 = max(Ret1, F[x] + Sum + Tmp1); // Pre
Ret2 = max(Ret2, F[x] - Sum + Tmp2); // Suf
Ret1 = max(Ret1, G[x]);
Tmp1 = max(Tmp1, F[x] - Sum);
Tmp2 = max(Tmp2, F[x] + Sum);
Sum += W[x], -- Out[x], x = To[x];
}
return max(Ret1, Ret2 + Sum);
}
int main () {
cin >> N;
for (int i = 1; i <= N; ++ i)
cin >> To[i] >> W[i], ++ In[To[i]], ++ Out[i];
for (int i = 1; i <= N; ++ i)
if (!In[i]) Q[++ T] = i;
while (H < T) {
++ H, -- Out[Q[H]];
#define Cost (W[Q[H]] + F[Q[H]])
G[To[Q[H]]] = max(G[To[Q[H]]], max(G[Q[H]], Cost + F[To[Q[H]]]));
F[To[Q[H]]] = max(F[To[Q[H]]], Cost);
#undef Cost
if (-- In[To[Q[H]]] == 0) Q[++ T] = To[Q[H]];
}
for (int i = 1; i <= N; ++ i)
if (Out[i]) Ans += GetV(i);
cout << Ans << endl;
return 0;
}
Luogu CF975D Ghosts
比较有趣的一个 \(Geometry?\) 迫真 \(Geometry!\)
前情提要:
/duel challenge @猪 2000 geometry \(from ~ Meatherm\)
然后 我们都没 \(Do\) 出来,\(Meatherm\) 真男人 \(Give ~ Up\) 了
最后被 \(zhicheng\) 三十秒钟爆切
思路部分
考虑拍照时 所有幽灵 在一条直线上,相当的规范!。
那么我们可以想到蛤,任意两只幽灵 横纵坐标差是成比例的,比值就是 \(a ~~ (\dfrac {y} {x})\)
这下好耍喽,如果要让两个幽灵 撅到一起,那么他们的 相对运动速度 也得满足这个比例噻。
也就是说 \(\dfrac {Vy_i - Vy_j} {Vx_i - Vx_j} = a\) (好好理解,蛤!)
然后简单变形就得到了 \(Vy_i - aVx_i = Vy_j - aVx_j\),把 \(i,j\) 分开了咩!
后头就好搞了噻,直接把每个 幽灵 的这坨东西 \(Vy_i - aVx_i\) 算出来。
阔到一个 \(unordered\_map\) 里头,然后对每只 幽灵 查询一遍,加个答案,就好了咩!
真的好了咩?如好!
我们少考虑喽一种情况得嘛,如果说啥子 \(Vx_i = Vx_j\),上头那个式子分母就莫得咯。
那不就瓜起!所以我们就额外记录一哈每个 幽灵 的 \(Vx\),开个两维的 \(unordered\_map\)。
每次加的时候跳过与自己 \(Vx\) 相等的 幽灵 就好了咩!
实现部分
按上面的思路,肯定有人要这么写嘛(就是我这个瓜货
unordered_map <long long, unordered_map<int, int> > mp;
for (int i = 1; i <= N; ++ i) {
for (auto Mea : mp[P[i].vy - a * P[i].vx])
Ans += Mea.second;
Ans -= mp[P[i].vy - a * P[i].vx][P[i].vx];
}
要这么写肯定给你 \(T\) 的哈起,要是所有的 幽灵 都在那儿 装怪。
然后 \(Vy_i - aVx_i\) 全都相等,那就完了噻,\(O(N^2)\) 喽!
啷个办嘛?要像这样!
for (auto i : mp) {
for (auto Mea : i.second) Sum += Mea.second;
for (auto Mea : i.second) Ans += Mea.second * (Sum - Mea.second);
Sum = 0;
}
很显然噻,阔以再优化一哈
for (auto i : mp) {
for (auto Mea : i.second) Ans -= 1ll * Mea.second * Mea.second, Sum += Mea.second;
Ans += Sum * Sum, Sum = 0;
}
完整代码
#include <bits/stdc++.h>
const int MAXN = 200005;
using namespace std;
struct Node {
int x, vx, vy;
} P[MAXN];
long long N, a, b, Sum, Ans;
unordered_map <long long, unordered_map<int, int> > mp;
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> a >> b;
for (int i = 1; i <= N; ++ i)
cin >> P[i].x >> P[i].vx >> P[i].vy;
for (int i = 1; i <= N; ++ i)
++ mp[P[i].vy - a * P[i].vx][P[i].vx];
for (auto i : mp) {
for (auto Mea : i.second) Ans -= 1ll * Mea.second * Mea.second, Sum += Mea.second;
Ans += Sum * Sum, Sum = 0;
}
cout << Ans << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号