平衡树小结
基础——二叉搜索树(BST)
二叉搜索树的定义:每个节点左儿子权值小于它的权值,右儿子权值大于它的权值。
用 BST 可以很容易维护一个有序的集合(或多重集),并支持插入删除、找排名、找数值、找前驱后继等操作。
在随机数据的情况下,BST 期望树高是 \(O(\log n)\) 的,但是极端情况会退化成链。
于是,平衡树应运而生。
\(\text{Treap}\)
\(\text{Treap}\) 是一种比较基础的平衡树。\(\text{Treap=Tree+Heap}\)。
除了满足 BST,\(\text{Treap}\) 给每个节点一个附加权值 \(pri\),并要求 \(pri\) 满足堆的性质。
可以证明,在 \(pri\) 随机的情况下,\(\text{Treap}\) 树高为 \(O(\log n)\)。
\(\text{Treap}\) 的实现方式有有旋与无旋两种。
有旋式 \(\text{Treap}\)
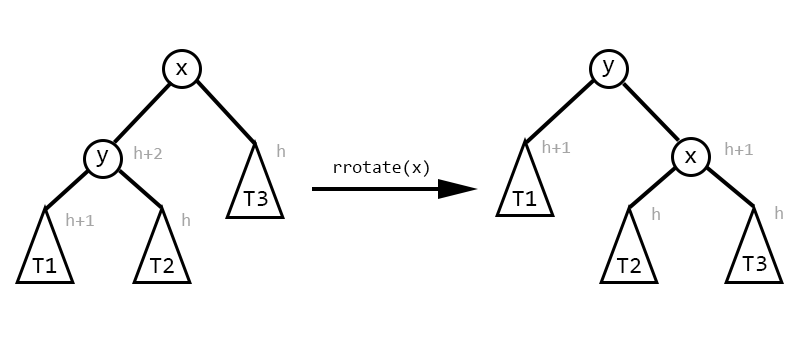
以小根堆为例。先放一张图:
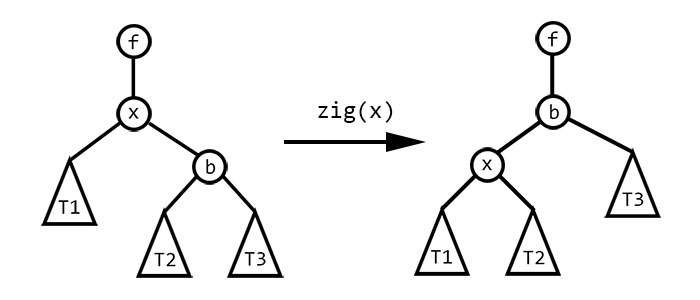
左旋操作(
zig)右旋同理
每次插入后递归向上处理,查看是否有出现儿子节点 \(pri\) 小于父亲节点 \(pri\) 的情况。如果\(pri_{rc}<pri_{x}\),则左旋 \(x\) 使 \(rc\) 转到 \(x\) 位置;如果 \(pri_{lc}<pri_{x}\),则右旋 \(x\) 使 \(lc\) 转到 \(x\) 位置。
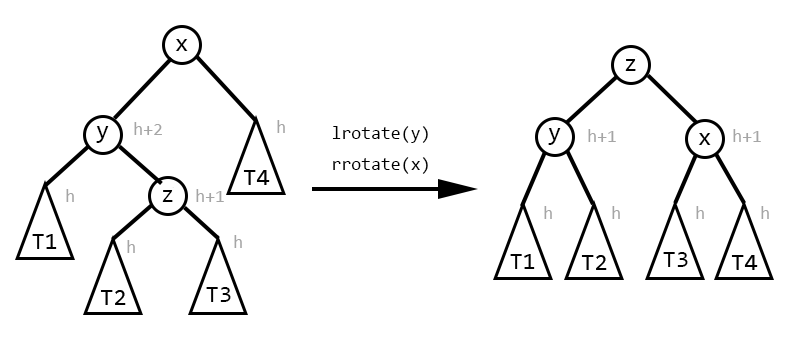
删除分三种情况:无子树、有一棵子树、有两棵子树。前两种都容易处理。第三种则可以通过 zig 和 zag,把左右儿子中 \(pri\) 较小的旋上来,把自己“沉”下去,转化为前两种情况。
无旋式 \(\text{Treap}\)
有两种操作:split 和 merge。
split 是可以根据某一个键值 \(k\) 或者一个大小 \(sz\) 来将树 \(i\) 分裂为两个树 \(x,\ y\)。其中 \(x\) 中所有值 \(\le k\),\(y\) 中所有值 \(>k\)。按照大小分裂也类似。
merge 是将两棵树 \(x,\ y\) 合并为一棵新树,要求 \(x\) 中所有元素都小于 \(y\) 中所有元素。
平衡树的基本操作都可以使用 split 和 merge 配合使用实现。
\(\textbf{Treap}\) 可以可持久化!
\(\text{Splay}\)
\(\text{Splay}\) 是一种保证均摊复杂度 \(O(\log n)\) 的平衡树。
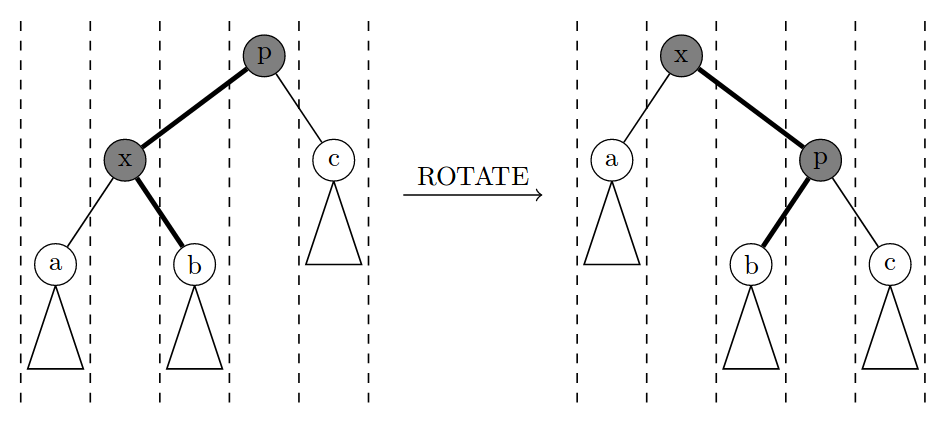
\(\text{Splay}\) 的
rotate
\(\text{Splay}\) 的旋转是把一个节点旋转到它的父亲的位置,splay 操作就是把一个节点不断向上旋转至根(或某个节点的儿子)。
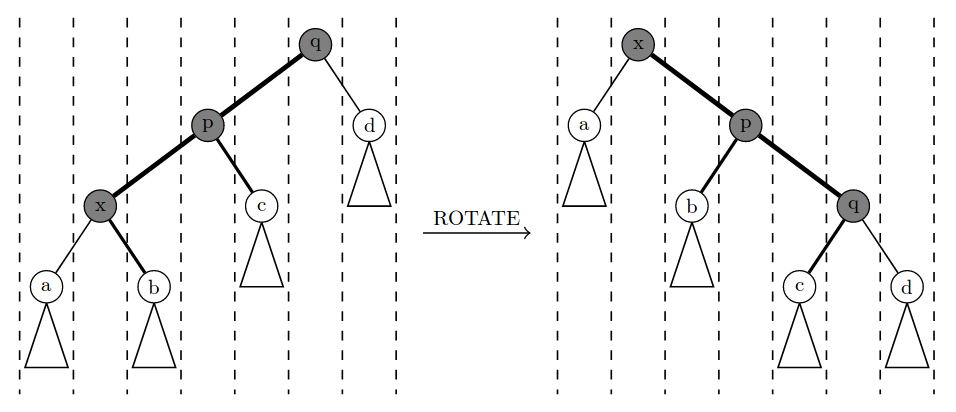
为了保证复杂度,splay 需要如此实现(\(i\) 为当前节点,\(f\) 为父亲,\(gf\) 为祖父):
- \(f\)、\(gf\)、\(i\) 共线,
rotate(f),rotate(i);
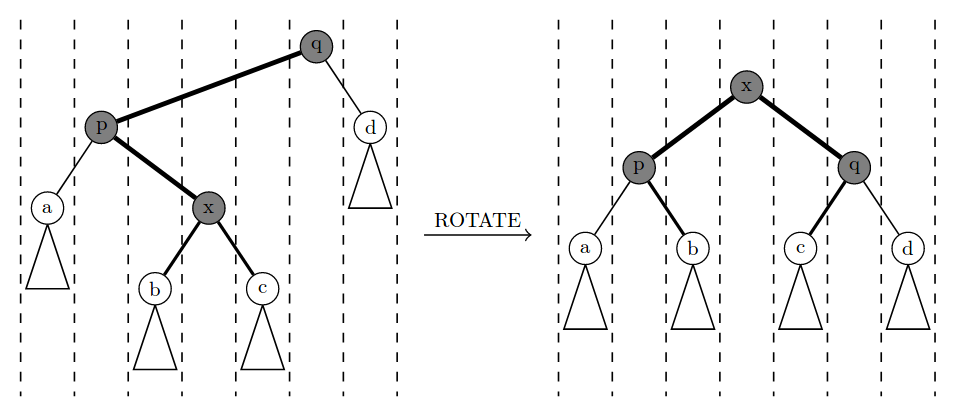
- \(f\)、\(gf\)、\(i\) 不共线,
rotate(i),rotate(i)。
每次插入、删除、查找后把找到的节点 splay 到根即可保证复杂度。
\(\text{AVL}\)
\(\text{AVL}\) 是一种很古老的平衡树,复杂度异常稳定,最坏情况下为 \(O(\log_\phi n)\)。
\(\text{AVL}\) 为满足一下性质的 BST:
- 定义叶子节点的 \(hgt\) 为 \(1\);
- 定义节点的 \(hgt\) 为 \(max(hgt_{lc},hgt_{rc})+1\);
- 每个节点满足 \(|hgt_{lc}-hgt_{rc}|\le 1\)。
复杂度证明:
设 \(S(h)\) 为树高为 \(h\) 的 \(\text{AVL}\) 树最少包含的节点数,那么 \(S(h)\) 的反函数 \(H(s)\) 就是节点数为 \(s\) 最大树高。
显然 \(S(h)\) 是一个增函数。
由 \(\text{AVL}\) 的性质得,若使得 \(S(h)\) 最小,则其两儿子的 \(hgt\) 为 \(h-1,\ h-2\)。
所以有:\(S(h)=S(h-1)+S(h-2)+1\)。
可得 \(S(h)\) 增长为指数级,所以 \(H(s)\) 增长是对数级的。
\(\text{AVL}\) 的插入删除与 BST 相同,但是需要每次递归自底向上使用左旋和右旋进行调整。
具体情况需要分 LL、LR、RR、RL 四种。
LL:左儿子的左子树插入节点
LL情况。灰色字为子树的 \(hgt\)。
只需执行一次右旋。
LR:左儿子的右子树插入节点
LR情况。灰色字为子树的 \(hgt\)。
需要一次左旋,一次右旋。
\(\text{RBT}\)
红黑树本质是一种 \(\text{B-Tree}\)。
红黑树为满足如下性质的 BST:
- 节点为红色或黑色;
- 根节点为黑色;
- 空节点为黑色;
- 每个红节点两个儿子均为黑节点;
- 每个空节点到根节点路径上经过的黑节点个数(黑高度)相等。
插入时将新节点作为红节点插入,保证满足性质 \(5\),但可能违反性质 \(4\),此时需要 insert-fixup。
删除时按照 BST 方式删除。如果删除的是黑节点,可能会违反性质 \(5\),此时需要 remove-fixup。
对于这两种 fixup 的讨论,我这里有一种巧妙的说明方法,可惜这里空间太小,写不下。
理论上红黑树可以可持久化!
平衡树的 \(\text{Leafy}\) 变种
我们知道线段树的 pushup 十分方便,因为每个节点的区间就是左右儿子区间的并。
我们知道平衡树的操作十分灵活,因为平衡的维护可以让我们肆无忌惮地插入节点。
那么有没有一种神奇的数据结构,集合了以上两种优点呢?
有,就是 \(\text{Leafy-Tree}\)。\(\text{Leafy-Tree}\) 的所有信息存储在叶子上,又有 \(n\) 个辅助节点,牺牲了一些空间换来了小常数和小码量。
一棵 BST 是如何变为 \(\text{Leafy-Tree}\) 的:
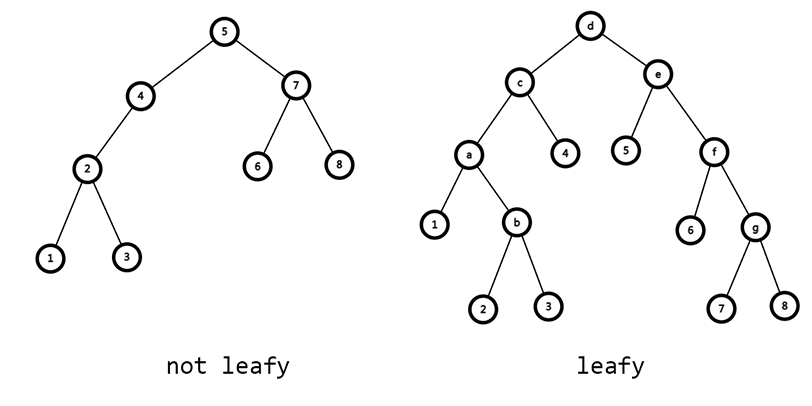
可能会有一篇文章专门讲讲 \(\text{Leafy Tree}\)。
平衡树的应用
平衡树最模板的应用就是维护有序集合。
但是利用中序遍历不变的特性,平衡树可以支持非常灵活的序列维护。准确来说,线段树可以做的平衡树都可以做,而平衡树在线段树的基础上还可以支持单点插入、单点删除、区间翻转、区间交换等操作,加上可持久化后还可以支持区间拷贝。(见 \(\text{Luogu P5586}\))
平衡树,尤其是 \(\text{Splay}\),可以用于维护多种动态树,如 \(\text{Link-Cut Tree}\)、\(\text{Top Tree}\)。它还可以在某些斜率优化 DP 中发挥作用。除此以外,会了平衡树可以让很多题的思维难度极度下降(当然代码量变多,但也没多多少不是吗),如 \(\text{CSP-J 2020 T2}\) 和 \(\text{CSP-J 2021 T2}\)。
总结
平衡树用途广泛,变化灵活,思想具有启发性,是必要也值得学习的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号