dfs及其简单应用

这里记录一下老师上课讲过的dfs.

主要思路是，我们对于每一个节点都设置白色、灰色和黑色三种颜色，分别表示三种状态：未访问、正在访问和访问完毕。这三种状态的标准是根据某一个具体节点的邻居节点来定的，就是说，对于某一个具体节点，如果还没有访问完该节点的所有邻居节点，那么就表示这个节点处于正在访问状态，如果所有邻居节点都访问完毕，那就表示这个节点已经访问完毕。

那么首先，为了简单起见，我们直接用一个二维数组来表示边，且在初始化的时候，所有节点到其他任何节点之间的距离都设置为无穷大，包括节点到它自己之间的距离。

void init()
{
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            edge[i][j] = INT_MAX;
        }
    }
}

然后，就可以开始dfs了。这个函数的参数只需要设置一个，表示当前正在访问的节点。首先，我们当然就是需要把这个节点的颜色设置为灰色啦！然后，我们开始访问它的所有邻居节点，一旦发现一个邻居节点并且这个邻居节点的颜色状态也是白色（表示未访问），那么就以这个邻居节点为基准，继续dfs.这就体现了深度的特点。等到全部访问完后，也就是这个节点的所有邻居节点都访问完毕了，那么就可以把这个节点的颜色设置为黑色了，最后就把它打印出来就可以了。

void dfs(int u)
{
    color[u] = "grey";
    for (int j = 1; j <= n; ++j) {
        if (edge[u][j] != INT_MAX && color[j] == "white") {
            dfs(j);
        }
    }
    color[u] = "black";
    cout << u << " ";
}

最后，为了防止访问的这个图是一个森林，我们还要来一个函数，遍历一遍这个图的所有节点，一旦发现有节点是白色的，那就访问。

void GraphTravel()
{
    for (int i = 1; i <= n; ++i) {
        if (color[i] == "white") {
            dfs(i);
        }
    }
}

最后来一波完整代码：

#include <iostream>
#include <algorithm>
#include <queue>
#define N 100
using namespace std;
queue<int> q;
int edge[N][N];
string color[N];
int n, edges;
void init()
{
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            edge[i][j] = INT_MAX;
        }
    }
}

void dfs(int u)
{
    color[u] = "grey";
    for (int j = 1; j <= n; ++j) {
        if (edge[u][j] != INT_MAX && color[j] == "white") {
            dfs(j);
        }
    }
    color[u] = "black";
    cout << u << " ";
}

void GraphTravel()
{
    for (int i = 1; i <= n; ++i) {
        if (color[i] == "white") {
            dfs(i);
        }
    }
}

int main()
{
    int start, end, weight;
    cout << "输入点的数量:" << endl;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        color[i] = "white";
    }
    cout << "输入边的数量:" << endl;
    cin >> edges;
    cout << "依次输入起点、终点和边的权值:" << endl;
    init();
    for (int i = 1; i <= edges; ++i) {
        cin >> start >> end >> weight;
        edge[start][end] = weight;
        edge[end][start] = weight;
    }
    GraphTravel();
    return 0;
}

再来一波运行效果：

 

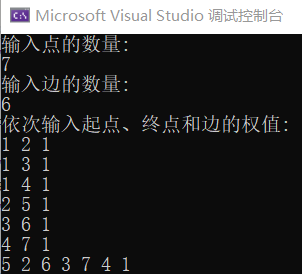
 对了，这个图长这样：

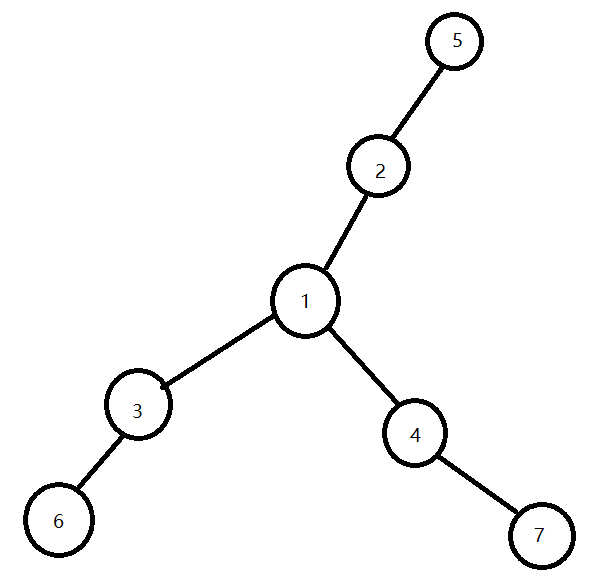
而如果要求这个图中有多少个不同的连通块，只要稍微改一下代码就可以了：

#include <iostream>
#include <algorithm>
#include <queue>
#define N 100
using namespace std;
queue<int> q;
int edge[N][N];
int color[N];
int n, edges;
void init()
{
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            edge[i][j] = INT_MAX;
        }
    }
}

void dfs(int u)
{
    color[u] = 2;
    for (int j = 1; j <= n; ++j) {
        if (edge[u][j] != INT_MAX && color[j] == 1) {
            dfs(j);
        }
    }
    color[u] = 3;
    cout << u << " ";
}

int GraphTravel()
{
    int count = 0;
    for (int i = 1; i <= n; ++i) {
        if (color[i] == 1) {
            count++;
            dfs(i);
        }
    }
    return count;
}

int main()
{
    int start, end, weight;
    cout << "输入点的数量:" << endl;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        color[i] = 1;
    }
    cout << "输入边的数量:" << endl;
    cin >> edges;
    cout << "依次输入起点、终点和边的权值:" << endl;
    init();
    for (int i = 1; i <= edges; ++i) {
        cin >> start >> end >> weight;
        edge[start][end] = weight;
        edge[end][start] = weight;
    }
    int num = GraphTravel();
    cout << endl;
    cout << "图中不同连通块的数目:" << num << endl;
    return 0;
}

（PS：颜色状态那里没有用string了，有种感觉说不上来，总感觉会出问题，所以改成用1,2,3来表示白灰黑了）

好了，现在，我们来用这个dfs判断一下有没有环：

这里，我们要借用并查集里面的思想，我们在访问节点的时候顺便设置一下父节点，例如，从1访问到2，那么2的父亲就是1.

这种情况下，我们需要对dfs函数稍作修改一下：

void dfs(int u)
{
    color[u] = 2;
    for (int j = 1; j <= n; ++j) {
        if (u != j && edge[u][j] != INT_MAX) {
            if (color[j] == 1) {
                father[j] = u;
                dfs(j);
            }
            else if (color[j] == 2 && father[u] != j) {
                hasCircle = true;
            }
        }
    }
    color[u] = 3;
    cout << u << " ";
}

你可能会问：为啥一会儿father[j]=u一会儿又father[u]!=j呢？没事，慢慢来！举个例子，我们从1访问到2：那么是不是当前u就是1？然后j就是2？因为1和1之间肯定没办法访问嘛。那么我就肯定需要把2的父亲设为1，也就是father[2] = 1.这个时候，就dfs(2)了，那么，2就变成u了！然后，for循环遍历再次遍历到1时，u=2，j=1.这个时候他俩换过来了！所以这个时候我判断一下father[2]是否等于1，因为这样才是判断有没有环的关键！正因为father[2] = 1所以下面那个else if语句才不会进去，要不然1和2,2和1，不管啥图都会有环的。

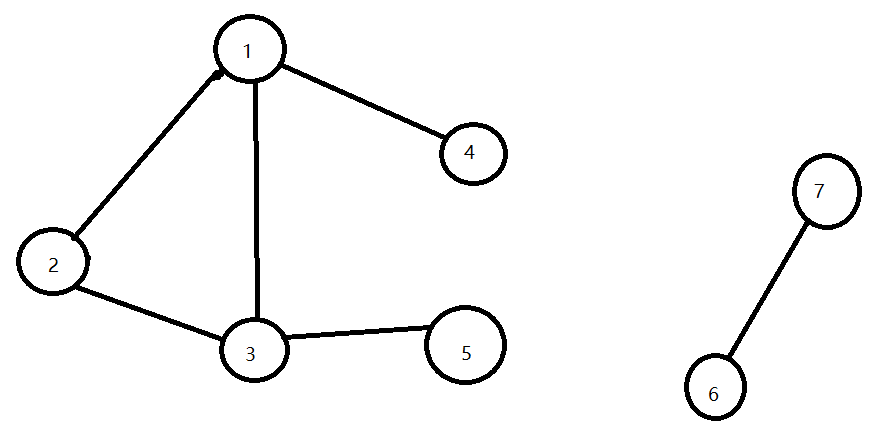
感觉这里还是说得不是很清楚，我们来个图说明一下：

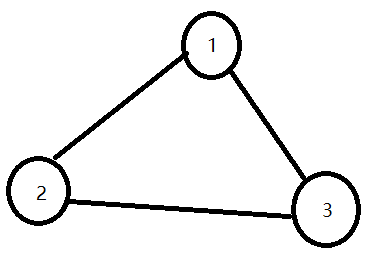
我们从1开始遍历，遍历到2，所以father[2] = 1.然后从2遍历到3，这个时候，father[3] = 2.最后，从3遍历到1，显然father[3]不等于1，因为我还没有为3设置父亲嘛。就算设置了，father[3]也不等于1，因为它会等于2！也就是说，father[2]=1,father[3]=2.那么这个时候，因为father[3]不等于1，所以肯定就会进入下面那个else if语句。那么，hasCircle就被设置为true了。感受一下这思路的巧妙！

 至于为什么现在的dfs代码比之前的要多了一个判断u不等于j和edge距离，害，憋说了，都是血泪教训！你不这么来一下，一来程序有可能判断自己和自己，二来有可能判断根本不存在边的两个节点，这都会导致代码出错。（脑子里闪过一个想法，是不是这里的if判断又可以优化一下？只是想想，可能可以。但今天太累了，不想想了，聪明的你一定可以想到！）

好吧我还是想了一下，那个u!=j应该可以去掉，不一定是对的，你可以测试一下。

好了，现在再贴一份完整代码，这里就需要先对father数组初始化了，其实也没变多少。

 

#include <iostream>
#include <algorithm>
#include <stack>
#define N 100
using namespace std;
stack<int>s;
int edge[N][N];
int color[N], father[N];
int n, edges;
bool hasCircle = false;
void init()
{
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            edge[i][j] = INT_MAX;
        }
    }
}

void dfs(int u)
{
    color[u] = 2;
    for (int j = 1; j <= n; ++j) {
        if (u != j && edge[u][j] != INT_MAX) {
            if (color[j] == 1) {
                father[j] = u;
                dfs(j);
            }
            else if (color[j] == 2 && father[u] != j) {
                hasCircle = true;
            }
        }
    }
    color[u] = 3;
    cout << u << " ";
}

int GraphTravel()
{
    int count = 0;
    for (int i = 1; i <= n; ++i) {
        if (color[i] == 1) {
            count++;
            dfs(i);
        }
    }
    return count;
}

int main()
{
    int start, end, weight;
    cout << "输入点的数量:" << endl;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        color[i] = 1;
        father[i] = 0;
    }
    cout << "输入边的数量:" << endl;
    cin >> edges;
    cout << "依次输入起点、终点和边的权值:" << endl;
    init();
    for (int i = 1; i <= edges; ++i) {
        cin >> start >> end >> weight;
        edge[start][end] = weight;
        edge[end][start] = weight;
    }
    int num = GraphTravel();
    cout << endl;
    cout << "图中不同连通块的数目:" << num << endl;
    if (hasCircle) {
        cout << "图中有环" << endl;
    }
    else {
        cout << "图中没有环" << endl;
    }
    return 0;
}

 

 

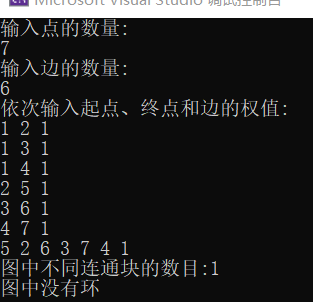
 这还是之前那个图，我们再来一个图测试一下：

 

 

 

 

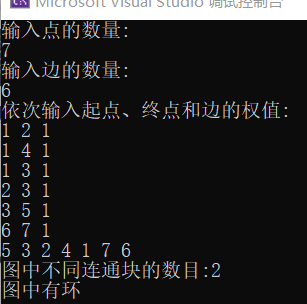
 完美！

 

 可能读者会对最后打印出来节点的顺序有所疑问，其实这是节点“变黑的顺序”，这个顺序很有用！具体有啥用呢？To be continued...