二叉搜索树
这次的二叉搜索树暂时只能添加、删除整数。
不同于以往创建树的过程,在创建一棵二叉搜索树时,我们还需要一个指向结点的父节点的指针(如果存在的话),静态内部类如下:
1 private TreeNode left; 2 private TreeNode right; 3 private TreeNode parent; 4 int val; 5 public TreeNode(int val, TreeNode parent) { 6 this.val = val; 7 this.parent = parent; 8 }
接着就开始逐步开发了!
最重要的几个方法莫过于添加元素、删除元素和遍历的方法。
我们先来看看添加元素的方法:
首先,应确定一点的是,二叉搜索树这样一种数据结构只是用来存储数据并方便查找的,那么外界人员在使用这样一种数据结构时,大概率是不会知道它的底层实现是二叉搜索树,所以我们提供给外部的接口中,添加元素的方法不应该出现任何与“结点”有关的东西,也就是说,方法的参数应该只是一个要添加的元素。
好了,我们正式开始分析代码:首先,我们方法里面应该判断一下这棵树的根结点是否存在。如果不存在,那么我们就创建一个根结点,其中根节点的父节点是null;如果存在,我们应从根节点开始,让该节点与二叉树中已经存在的节点一个接一个地进行比较。小,则找左子树;否则找右子树。
我们可以把比较的过程写成一个私有方法,也便于记录比较结果。
1 public void add(int val) { 2 if(root == null){ 3 root = new TreeNode(val, null); //根结点没有父结点 4 ++size; 5 return; 6 } 7 int cmp = 0; //声明在外面是因为我们需要知道比较结果 8 TreeNode node = root; 9 TreeNode parent = root; //记录方向 10 while(node != null) 11 { 12 cmp = compare(val, node.val); 13 parent = node; //如果没有parent,退出循环后node为空,不便于接下来的操作 14 if(cmp > 0){ 15 node = node.right; 16 }else if(cmp < 0){ 17 node = node.left; 18 }else{ 19 return; 20 } 21 } 22 TreeNode newNode = new TreeNode(val, parent); 23 if(cmp < 0){ //比较结果在这里就派上用场了 24 parent.left = newNode; 25 }else{ 26 parent.right = newNode; 27 } 28 ++size; 29 }
1 private int compare(int e1, int e2) { 2 return (e1 - e2); 3 }
再来看看删除方法:
由于外界并不知道我们底层采用的是二叉搜索树,因此在调用时,他们肯定只会使用需要删除的那个数作为删除方法的参数。然而在我们内部,我们需要删除一个数,需要先找到这个数,也就是先找到这个结点,然后删除这个结点。所以我们需要在提供给外部的删除方法中使用两个方法完成这一件事,即getNode()和removeNode()方法。
getNode():
1 private TreeNode getNode(int val){ 2 TreeNode node = root; 3 int cmp = 0; 4 while(node != null) 5 { 6 cmp = compare(val, node.val); 7 if(cmp == 0){ 8 return node; 9 }else if(cmp < 0) { 10 node = node.left; 11 }else{ 12 node = node.right; 13 } 14 } 15 return null; 16 }
找到节点后,我们自然需要删除结点。删除的话,有几种情况需要考虑,那就是这个节点,可能是叶子结点,也可能是度为1的结点或者度为2的结点。
对于叶子结点,大多数情况下我们想到的就是普通的叶子结点,其实还有一种情况,那就是叶子结点就是根结点,也就是这棵二叉搜索树只有一个结点。这样一来,而度为1的结点也有可能是根结点。这是所有我们需要考虑的情况。
我们首先考虑度为2的结点的删除。首先不管这个度为2的结点是不是根结点,它的左子树所有元素一定比右子树小,它自己则夹在中间。那么这个时候,我们的处理方法是,寻找这个节点的直接前驱结点或直接后继结点来代替它。直接前驱或直接后继就是在中序遍历顺序中该结点的前面那个元素或后面那个元素。如果是直接前驱,那么这个前驱结点的值一定是待删节点的左子树中最大的点,那我们需要不停地在其左子树中找右孩子。找到后,这个右孩子可能是叶子结点,也有可能度为1(这种情况下,该结点只有左孩子,没有右孩子,否则它就不是最大的),但绝对不可能度为2,若度为2,那么它一定不是最大的,这种情况下我们仍然需要寻找其右孩子。因此,倘若待删节点度为2,我们先找其直接前驱或直接后继(后继就是其右子树的最小值),然后替代一波,再删掉结点就可以了,这时,我们就可以把删节点的代码统一放在一个地方。
对于度为1的结点,若是根结点,取消root对其指向关系即可。否则我们仍需知道该结点是其父节点的左孩子还是右孩子。
对于叶子结点而言,如果是根结点,直接root=null就行。其他情况,我们需要知道这个叶子节点是其父节点的左孩子还是右孩子,知道后,直接删。
代码如下:
首先是找直接后继:
1 private TreeNode successor(TreeNode node) { 2 if(node == null){ 3 return null; 4 } 5 TreeNode cur = node.right; 6 if(cur != null){ 7 while(cur.left != null) 8 { 9 cur = cur.left; 10 } 11 return cur; 12 } 13 while(node.parent != null && node.parent.right == node) 14 { 15 node = node.parent; 16 } 17 return node.parent; 18 }
其次是删除节点:
1 private void removeNode(TreeNode node) { 2 if (node == null) { 3 return; 4 } 5 if (node.hasTwoChildren()) { //单独讨论删除度为2的结点的情况,最后一起删除 6 TreeNode succ = successor(node); 7 node.val = succ.val; 8 node = succ; //这样一来,我就只用把删除节点的工作全部放在下面,上面就不用管了 9 } 10 TreeNode replacement = node.left != null ? node.left : node.right; 11 if(replacement != null){ //node度为1 12 replacement.parent = node.parent; 13 if(node.parent == null){ //node是度为1的根结点 14 root = replacement; 15 }else if(node == node.parent.left){ 16 node.parent.left = replacement; 17 }else{ 18 node.parent.right = replacement; 19 } 20 }else if(node.parent == null){ //node是度为0的根结点 21 root = null; 22 }else{ //node是度为0的叶子结点 23 if(node == node.parent.left){ 24 node.parent.left = null; 25 }else{ 26 node.parent.right = null; 27 } 28 } 29 --size; 30 }
这时,我们就还需要一个判断结点是不是度为2的结点的方法,这个方法我们直接写在内部类里面:
1 public boolean hasTwoChildren() { 2 if (left != null && right != null) { 3 return true; 4 } 5 return false; 6 }
剩下的就很简单了。无非是一些判断用户输入的数据是否存在,以及存储了数据的大小的函数。
来一波完整代码:
BinarySearchTree.java:
1 package com.hw.list0710; 2 3 public class BinarySearchTree { 4 private int size = 0; 5 private TreeNode root; 6 private static class TreeNode { 7 private TreeNode left; 8 private TreeNode right; 9 private TreeNode parent; 10 int val; 11 public TreeNode(int val, TreeNode parent) { 12 this.val = val; 13 this.parent = parent; 14 } 15 16 /** 17 * 判断是否是度为2的结点 18 * @return 19 */ 20 public boolean hasTwoChildren() { 21 if (left != null && right != null) { 22 return true; 23 } 24 return false; 25 } 26 } 27 28 /** 29 * 返回二叉搜索树的大小 30 * @return 31 */ 32 public int size(){ 33 return size; 34 } 35 36 /** 37 * 删除节点时先定位到需要删除的节点 38 * @param val 39 * @return 40 */ 41 private TreeNode getNode(int val){ 42 TreeNode node = root; 43 int cmp = 0; 44 while(node != null) 45 { 46 cmp = compare(val, node.val); 47 if(cmp == 0){ 48 return node; 49 }else if(cmp < 0) { 50 node = node.left; 51 }else{ 52 node = node.right; 53 } 54 } 55 return null; 56 } 57 58 /** 59 * 查看某元素是否存在 60 * @param e 61 * @return 62 */ 63 public boolean contains(int e) { 64 if(getNode(e) != null){ 65 return true; 66 } 67 return false; 68 } 69 70 /** 71 * 比较两个元素的大小 72 * @param e1 73 * @param e2 74 * @return 75 */ 76 private int compare(int e1, int e2) { 77 return (e1 - e2); 78 } 79 80 /** 81 * 向二叉搜索树中添加元素 82 * @param val 83 */ 84 public void add(int val) { 85 if(root == null){ 86 root = new TreeNode(val, null); //根结点没有父结点 87 ++size; 88 return; 89 } 90 int cmp = 0; //声明在外面是因为我们需要知道比较结果 91 TreeNode node = root; 92 TreeNode parent = root; //记录方向 93 while(node != null) 94 { 95 cmp = compare(val, node.val); 96 parent = node; //如果没有parent,退出循环后node为空,不便于接下来的操作 97 if(cmp > 0){ 98 node = node.right; 99 }else if(cmp < 0){ 100 node = node.left; 101 }else{ 102 return; 103 } 104 } 105 TreeNode newNode = new TreeNode(val, parent); 106 if(cmp < 0){ //比较结果在这里就派上用场了 107 parent.left = newNode; 108 }else{ 109 parent.right = newNode; 110 } 111 ++size; 112 } 113 114 /** 115 * 找后继结点 116 * @param node 117 * @return 118 */ 119 private TreeNode successor(TreeNode node) { 120 if(node == null){ 121 return null; 122 } 123 TreeNode cur = node.right; 124 if(cur != null){ 125 while(cur.left != null) 126 { 127 cur = cur.left; 128 } 129 return cur; 130 } 131 while(node.parent != null && node.parent.right == node) 132 { 133 node = node.parent; 134 } 135 return node.parent; 136 } 137 138 /** 139 * 删除结点 140 * @param node 141 */ 142 private void removeNode(TreeNode node) { 143 if (node == null) { 144 return; 145 } 146 if (node.hasTwoChildren()) { //单独讨论删除度为2的结点的情况,最后一起删除 147 TreeNode succ = successor(node); 148 node.val = succ.val; 149 node = succ; //这样一来,我就只用把删除节点的工作全部放在下面,上面就不用管了 150 } 151 TreeNode replacement = node.left != null ? node.left : node.right; 152 if(replacement != null){ //node度为1 153 replacement.parent = node.parent; 154 if(node.parent == null){ //node是度为1的根结点 155 root = replacement; 156 }else if(node == node.parent.left){ 157 node.parent.left = replacement; 158 }else{ 159 node.parent.right = replacement; 160 } 161 }else if(node.parent == null){ //node是度为0的根结点 162 root = null; 163 }else{ //node是度为0的叶子结点 164 if(node == node.parent.left){ 165 node.parent.left = null; 166 }else{ 167 node.parent.right = null; 168 } 169 } 170 --size; 171 } 172 173 /** 174 * 删除数据 175 * @param val 176 */ 177 public void remove(int val) { 178 removeNode(getNode(val)); 179 } 180 181 /** 182 * 线索遍历二叉搜索树(内部方法) 183 * @param cur 184 */ 185 private void morrisOrder(TreeNode cur){ 186 if(cur == null){ 187 return; 188 } 189 TreeNode mostRight = null; 190 while(cur != null) 191 { 192 mostRight = cur.left; 193 if(mostRight != null){ 194 while(mostRight.right != null && mostRight.right != cur) 195 { 196 mostRight = mostRight.right; 197 } 198 if(mostRight.right == null){ 199 mostRight.right = cur; 200 cur = cur.left; 201 continue; 202 }else{ 203 System.out.print(cur.val+" "); 204 mostRight.right = null; 205 } 206 }else{ 207 System.out.print(cur.val+" "); 208 } 209 cur = cur.right; 210 } 211 } 212 213 /** 214 * 遍历二叉搜索树 215 */ 216 public void order() { 217 morrisOrder(root); 218 } 219 }
这里我们写一个测试类:
TestTree.java:
1 package com.hw.list0710; 2 3 public class TestTree { 4 public static void main(String[] args) { 5 long start = System.currentTimeMillis(); 6 BinarySearchTree bst = new BinarySearchTree(); 7 System.out.print("添加7:"); 8 bst.add(7); 9 bst.order(); 10 System.out.println(); 11 System.out.print("添加10:"); 12 bst.add(10); 13 bst.order(); 14 System.out.println(); 15 System.out.print("添加3:"); 16 bst.add(3); 17 bst.order(); 18 System.out.println(); 19 System.out.print("添加19:"); 20 bst.add(19); 21 bst.order(); 22 System.out.println(); 23 System.out.print("添加5:"); 24 bst.add(5); 25 bst.order(); 26 System.out.println(); 27 System.out.println("判断是否存在元素11:"); 28 System.out.print("判断结果:"); 29 System.out.println(bst.contains(11)); 30 System.out.print("添加元素11:"); 31 bst.add(11); 32 bst.order(); 33 System.out.println(); 34 System.out.println("判断是否存在元素11:"); 35 System.out.print("判断结果:"); 36 System.out.println(bst.contains(11)); 37 System.out.print("添加8:"); 38 bst.add(8); 39 bst.order(); 40 System.out.println(); 41 System.out.println("此时二叉搜索树的大小为:"+bst.size()); 42 System.out.print("删除元素10:"); 43 bst.remove(10); 44 bst.order(); 45 System.out.println(); 46 System.out.println("此时二叉搜索树的大小为:"+bst.size()); 47 long end = System.currentTimeMillis(); 48 System.out.println("总耗时:"+(end-start)+"毫秒"); 49 } 50 }
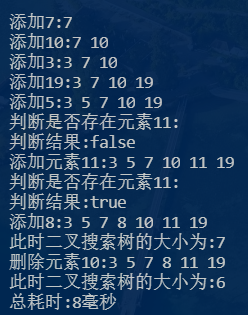
看看效果:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号