N皇后问题

https://www.bilibili.com/video/BV1ZK411K7A8?t=794

首先十分感谢B站小姐姐精彩的讲课内容，再结合一位兄弟通俗易懂的代码，我写了这份java版的N皇后问题的代码，供大家也供自己参考学习。

我们以四皇后问题为例，其主要思路就是：在这个4×4的棋盘上，我们每放置一个皇后，那么就把这个点标记为已放置皇后，然后把该皇后的所在行、所在列以及所在的两条对角线的所有点全部标记为其可攻击位，再递归地从第二行开始重复上一过程，寻找未被标记为可攻击位的点放置皇后。若不存在这样的点，那么就说明我们上一步放置皇后的位置是有误的，所以这时候就需要回到上一状态重新放置位置，这个过程，我们称之为回溯法。

其中，我们可以用一个n×n的数组来存储攻击位，再用一个char类型的二维数组存储哪些点放置了皇后，其中，‘Q’表示该点放置了皇后，‘.’表示该点未放置皇后。

现在我们来看看实现这个问题的一些方法：

private void copy(int[][] arr, int[][] val, int n){
        for(int i = 0;i < n;++i){
            for(int j = 0;j < n;++j){
                arr[i][j] = val[i][j];
            }
        }
    }

这个是用来备份的，我们想要回溯，就需要回到上一状态，那么如何寻找上一状态呢？在放置皇后之前，我们需要备份当前的已标记攻击位的所有点和已放置了皇后的所有点。这个方法就是用来实现这个的。

private void print(int n){
        for(int i = 0;i < n;++i){
            for(int j = 0;j < n;++j){
                System.out.print(queen[i][j]+" ");
            }
            System.out.println();
        }
        System.out.println();
    }

这个方法是用来打印最终棋盘的，使棋盘可视化。

private void updateAttack(int x, int y, int n){  
        int[] dx = {-1, -1, -1, 0, 1, 1, 1, 0};  //行方向
        int[] dy = {-1, 0, 1, 1, 1, 0, -1, -1};  //列方向
        attack[x][y] = 1;
        for(int i = 1;i < n;++i){
            for(int j = 0;j < 8;++j){
                int nx = x + i * dx[j];
                int ny = y + i * dy[j];
                if(nx >= 0 && nx < n && ny >= 0 && ny < n){
                    attack[nx][ny] = 1;
                }
            }
        }
    }

这个方法用来实现更新攻击位数组，即attack数组。我们需要设置八个方向（上下左右左上左下右上右下）。至于为什么dx和dy数组是那样的，我们可以这么想：假设一个点的坐标是(x,y),那么其上面的点的坐标就是(x-1,y)，右边的点(x,y+1),左边的点(x,y-1),下面的点(x+1,y).其余位置可以类似地推导出来。

然后，我们需要以当前点为起始坐标点，从八个方向向外延伸，这也就是两层for循环的由来。由于初始化attack数组时里面所有的元素都为0，因此标记攻击位时我们就把值设为1.

public void init(int n){
        for(int i = 0;i < n;++i){
            for(int j = 0;j < n;++j){
                attack[i][j] = 0;
                queen[i][j] = '.';
            }
        }
    }

这个方法很简单，就是用来初始化棋盘的。

 public void dfs(int k, int n){
        if(k == n){
            print(n);
            count++;
            return;
        }
        for(int i = 0;i < n;++i){  //这个for循环可以保证程序尝试各种可能的摆法
            if(attack[k][i] == 0){
                int[][] temp = new int[10][10];
                copy(temp, attack, n); //先备份
                queen[k][i] = 'Q'; //在这个位置放置皇后
                updateAttack(k, i, n); // 因为上一步放置了皇后，所以需要更新attack数组
                dfs(k + 1, n); //递归下一行，继续放置皇后
                copy(attack, temp, n); //递归完成后，需要回溯，因此需要回到原来的状态
                queen[k][i] = '.';
            }
        }
    }

这个就是核心代码了。k表示行数，也就是皇后数，一旦k与n相等，就表示我们找到了一组解，这个时候就把解的数量自增。如果不相等，这很正常。我们就要通过一个for循环，遍历这个棋盘所有的列。备份数组、放置皇后、更新攻击位、这些都做完后，遍历下一行，重复以上工作。同时还要回溯，遍历完后，如果下一行没有解，那么我们是需要回到原来的状态的，所以递归后我们还需要复原，回到原来的状态。如果找到了解，没关系，解的数量增加后方法照样会return，这个时候我们就需要接着找下一组解。所以也还是需要回到原来的状态。

试想一下，如果不回到原来的状态，那么在错误的位置上占据着皇后，是不是我们永远也无法接近真相了？所以狠的时候必须要狠，把错误位置的皇后去掉。

来一波完整代码：

package com.hw.list0710;

import java.util.Scanner;

public class Queens {
    private int[][] attack = new int[10][10];
    private char[][] queen = new char[10][10];
    public static int count;
    /**
     * 拷贝数组，用来备份
     * @param arr
     * @param val
     * @param n
     */
    private void copy(int[][] arr, int[][] val, int n){
        for(int i = 0;i < n;++i){
            for(int j = 0;j < n;++j){
                arr[i][j] = val[i][j];
            }
        }
    }

    /**
     * 打印放置了皇后的棋盘
     * @param n
     */
    private void print(int n){
        for(int i = 0;i < n;++i){
            for(int j = 0;j < n;++j){
                System.out.print(queen[i][j]+" ");
            }
            System.out.println();
        }
        System.out.println();
    }

    /**
     * 设置皇后的攻击方向
     * @param x
     * @param y
     * @param n
     */
    private void updateAttack(int x, int y, int n){  
        int[] dx = {-1, -1, -1, 0, 1, 1, 1, 0};  //行方向
        int[] dy = {-1, 0, 1, 1, 1, 0, -1, -1};  //列方向
        attack[x][y] = 1;
        for(int i = 1;i < n;++i){
            for(int j = 0;j < 8;++j){
                int nx = x + i * dx[j];
                int ny = y + i * dy[j];
                if(nx >= 0 && nx < n && ny >= 0 && ny < n){
                    attack[nx][ny] = 1;
                }
            }
        }
    }

    /**
     * 初始化棋盘
     * @param n
     */
    public void init(int n){
        for(int i = 0;i < n;++i){
            for(int j = 0;j < n;++j){
                attack[i][j] = 0;
                queen[i][j] = '.';
            }
        }
    }

    /**
     * 放置皇后的核心代码
     * @param k
     * @param n
     */
    public void dfs(int k, int n){
        if(k == n){
            print(n);
            count++;
            return;
        }
        for(int i = 0;i < n;++i){  //这个for循环可以保证程序尝试各种可能的摆法
            if(attack[k][i] == 0){
                int[][] temp = new int[10][10];
                copy(temp, attack, n); //先备份
                queen[k][i] = 'Q'; //在这个位置放置皇后
                updateAttack(k, i, n); // 因为上一步放置了皇后，所以需要更新attack数组
                dfs(k + 1, n); //递归下一行，继续放置皇后
                copy(attack, temp, n); //递归完成后，需要回溯，因此需要回到原来的状态
                queen[k][i] = '.';
            }
        }
    }

    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        Queens queen = new Queens();
        count = 0;
        int n = s.nextInt();
        s.close();
        queen.init(n);
        queen.dfs(0, n);
        System.out.println("摆法共有:"+count+"种");
    }
}

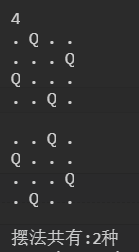
来看看效果：