二分查找

二分查找

二分查找分为整数二分和小数二分，其中整数二分涉及的边界问题比较多，理解起来相对复杂。

# 整数二分

如果可以找到一个性质，可以把区间一分为二，一半满足性质一半不满足。二分可以找到这个性质的边界，可以是①也可以是②。

这里这个分界点①和②就分两种情况讨论。

# 寻找边界点①——右边界

  1. mid = (l + r + 1) >> 1

  2. if( check(mid) ) 有两种结果

    • true >>> [mid, r] >>> l = mid

      mid满足性质，因此mid落在红色区间，并且在红色区间可以取到边界点①，因此下一个区间包含mid，区间为[mid, r]。

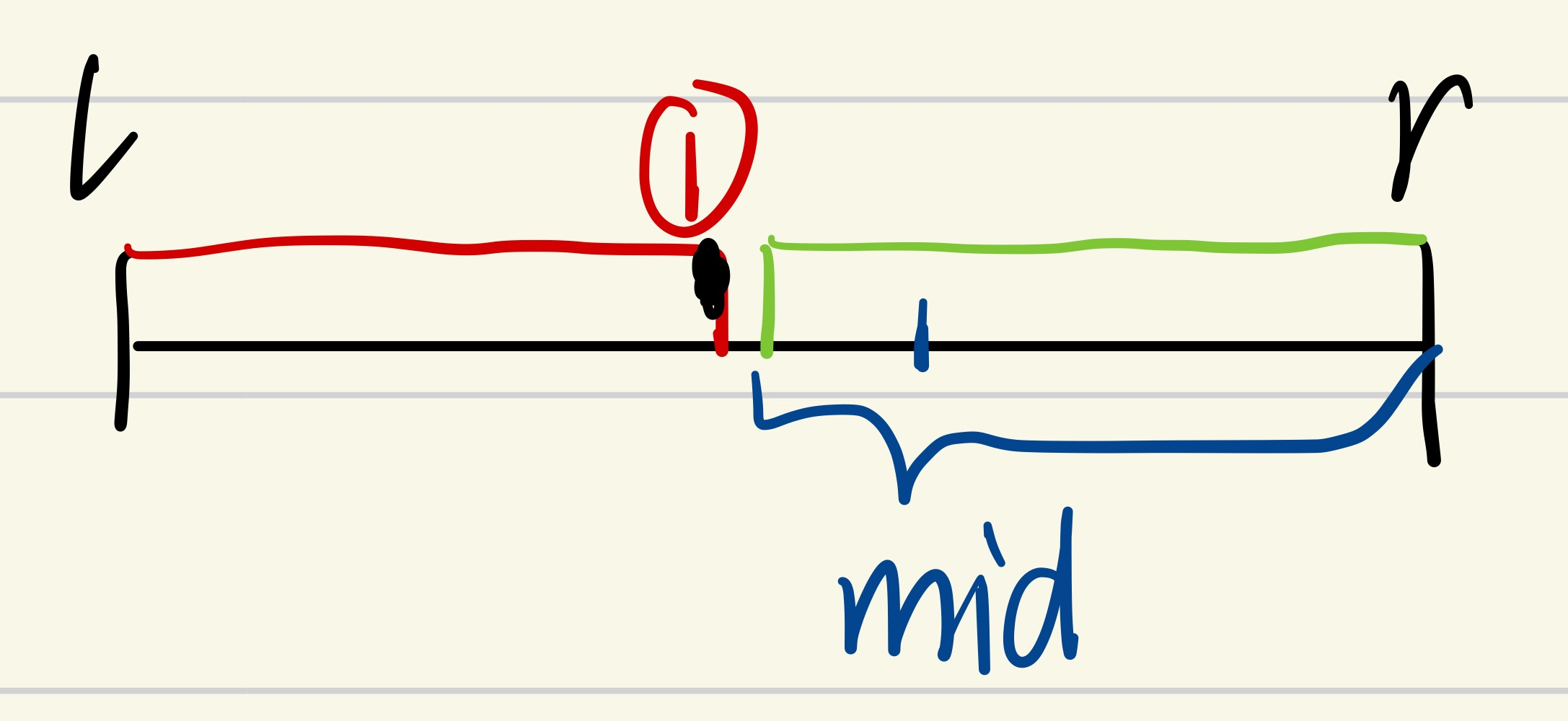
    • false >>> [l, mid - 1] >>> r = mid - 1

      mid不满足性质，因此mid落在绿色区间，在绿色区间内不可能取到边界点①，因此下一个区间不包含mid，区间为[l, mid - 1]。

# 寻找边界点②——左边界

  1. mid = (l + r) >> 1

  2. if ( check(mid) ) 有两种结果

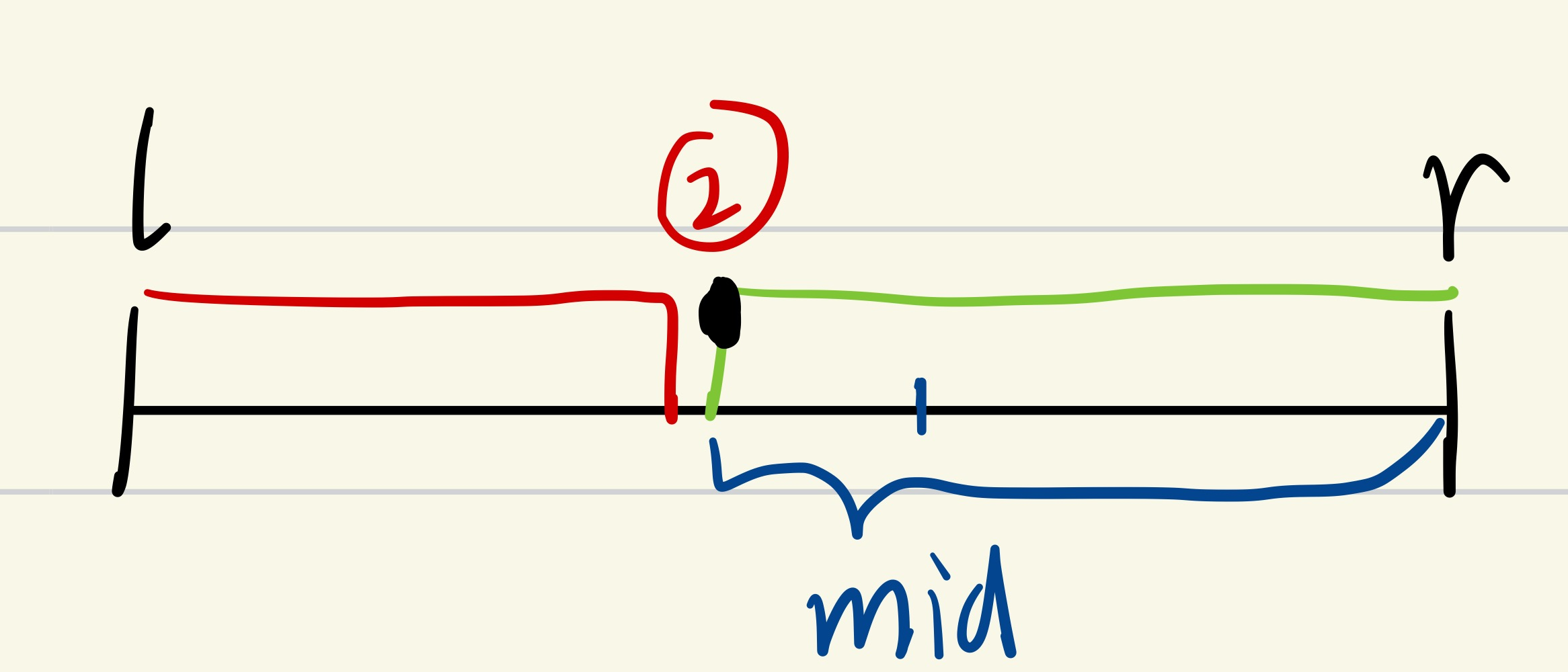
    • true >>> [l, mid] >>> r = mid

      mid满足性质，因此mid落在绿色区间，并且在绿色区间内可以取到边界点②，所以下一个区间包含mid，区间为[l, mid]。

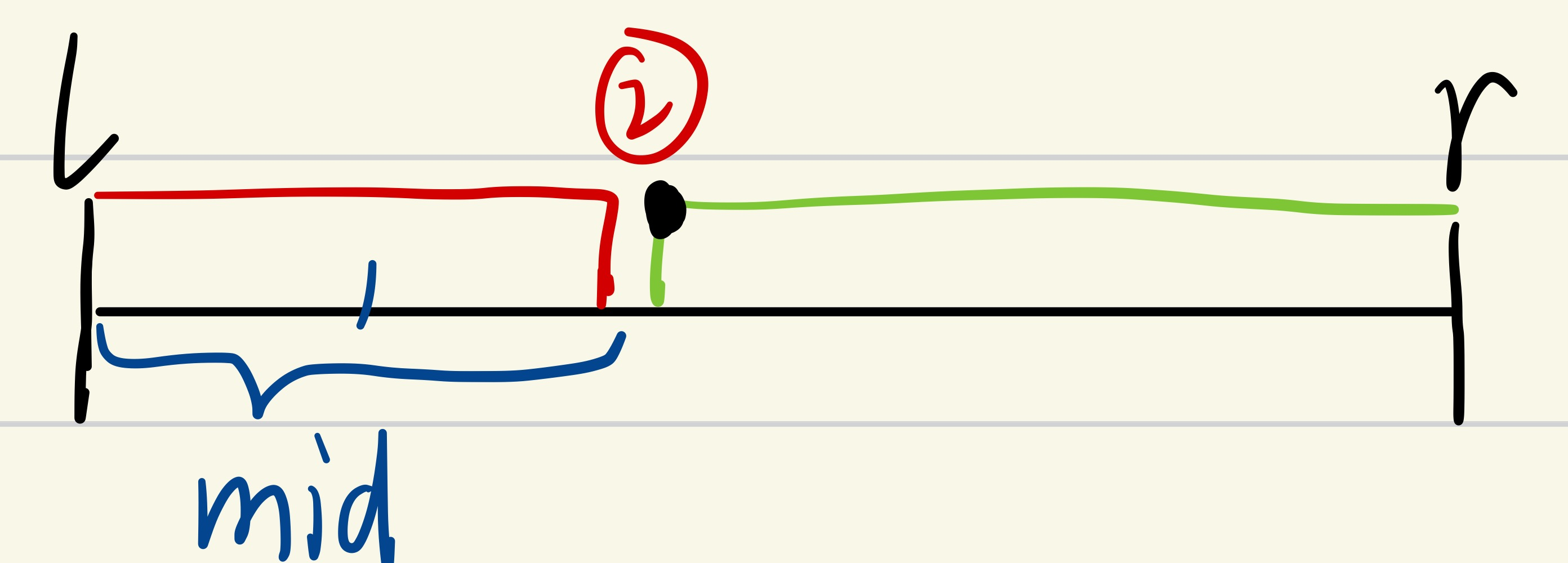
    • false >>> [mid + 1, r] >>> l = mid + 1

      mid不满足性质，因此mid落在红色区间，并且在红色区间内不可能取到边界点②，所以下一个区间不包含mid，区间为[mid + 1, r]。

# 步骤

一般情况下，先写一个mid的取值，然后再写check()函数的实现，及需要满足的性质。根据check()的返回值判断区间如何划分。

A. 先确定序列的上下界

int l = 0, r = n - 1;

B. 开始查找，直接写出一个mid，之后再看看用不用+1

int l = 0, r = n - 1;
while( l < r ) {
    int mid = l + r >> 1;
}

C. 判断是要找性质的左边界还是右边界。

比如找左边界，即第一个>=x的数。这里就开始讨论两种区间更新的情况，可以直接画出序列上面满足性质和不满足性质的区间图，然后再判断l, r的更新方式。

  1. 如果mid落在>=x的区间上，则x在mid的左边，同时mid和x在同个区间上，因此收缩r时r = mid
  2. 如果mid没有落在>=x的区间上，则x在mid的右边，而且mid和x不在同一个区间上，因此收缩l时l = mid + 1

最后再看看mid的更新方式要不要+1，可以直接记：寻找性质左边界时不需要 +1，或者是当更新区间的时候如果没有出现l, r其中一个更新为“mid - 1”，则不用在前面+ 1。

int l = 0, r = n - 1;
while( l < r ) {
    int mid = l + r >> 1;
    if(q[mid] >= x)  r = mid;
    else l = mid + 1;
}

D. 在查找结束后，l和r会重叠指向我们要查找的性质的边界。若目标x存在，则可以直接输出x的位置。若目标不存在，则会返回第一个大于x的数。

int l = 0, r = n - 1;
while( l < r ) {
    int mid = l + r >> 1;
    if(q[mid] >= x)  r = mid;
    else l = mid + 1;
}	//then l == r
if(q[l] == x) cout << l << endl;

# 需要斟酌的细节

mid = (l + r) >> 1 还是 mid = (l + r + 1) >> 1

还是这个图

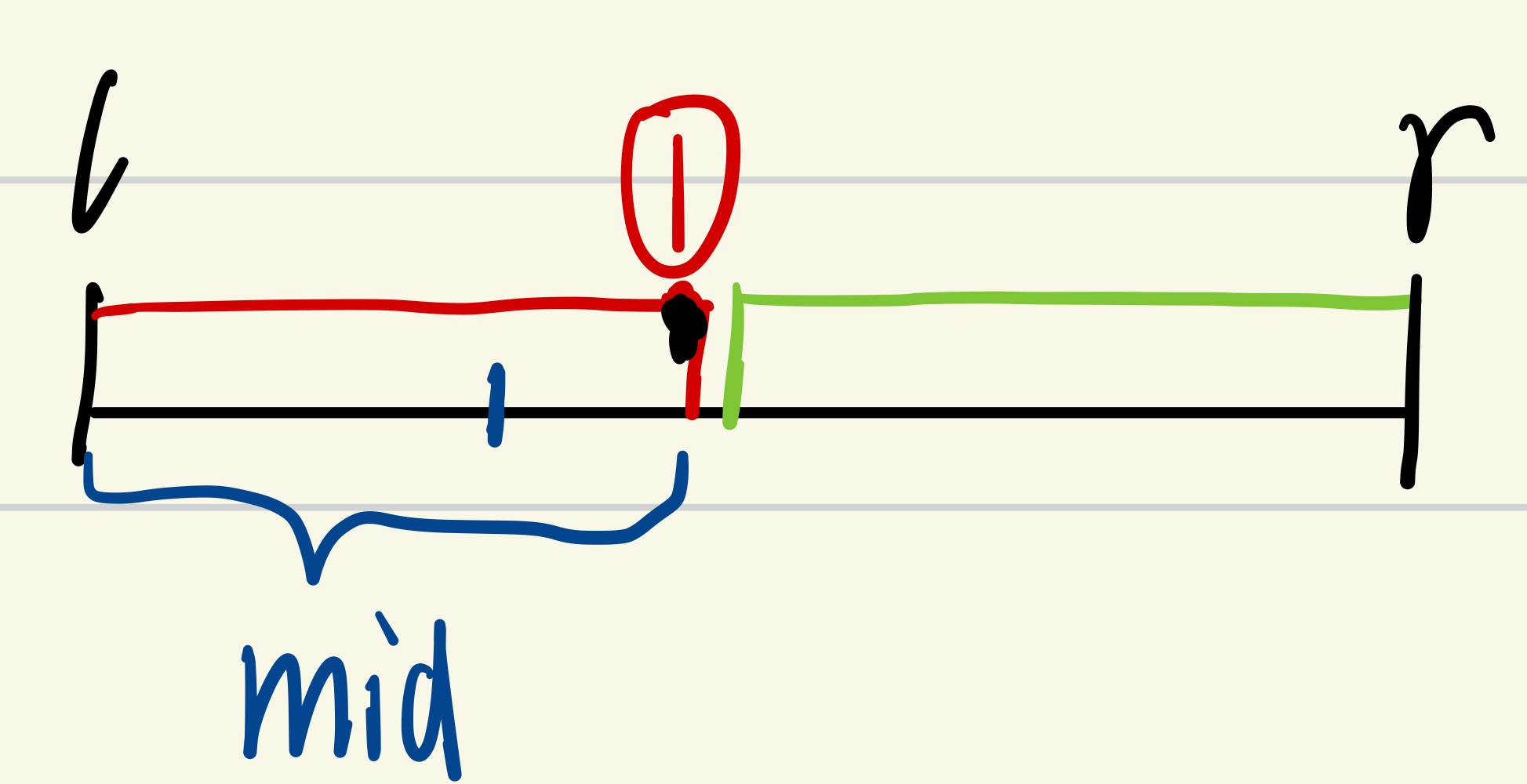
在寻找边界点①的时候，当更新到l + 1= r的时候，即l与r相邻时，如果mid满足红色性质，则更新区间为[mid, r]，也就是把l更新成mid。

如果使用mid = (l + r) >> 1，由于整数除法是下取整， 因此把l更新成mid会有：l = mid = (l + (l+1) ) >> 1 = (2l + 1) >> 1 = l.

也就是l = l，相当于没有更新区间，因此会不停的执行mid = (l + r) >> 1， l = mid陷入死循环。

因此需要使用mid = (l + r + 1) >> 1使得mid的结果是区间的一半的上取整。这样区间的左边界才会收缩。

可以这么理解记忆：

  • 当寻找性质的左边界的时候，由于更新区间为r = mid, l = mid + 1，此时mid = l + r >> 1，不需要加一。

    • 为什么？
    • 因为不加一的时候mid是下取整
    • 更新r时直接赋值为mid的也会下取整，因此r一定会收缩，不会死循环。
    • 更新l时是赋值为mid + 1会上取整，因此l也一定会收缩，所以mid不需要加一。

  • 当寻找性质的右边界的时候，由于更新区间为l = mid, r = mid - 1，此时mid = l + r + 1 >> 2，需要加一。

    • 为什么？
    • 因为加一的时候mid是上取整
    • 更新l时直接赋值为mid也会上取整，因此l一定会收缩，不会死循环。
    • 更新r时赋值为mid - 1会抵消掉上取整，因此r也一定会收缩。

# 查找结束时 l 和 r 的位置

由于循环的条件时l < r，然后更新区间都会在[l, r]之间更跟新，因此最终循环结束时必定有l == r，因此最终的结果在 l 或者 r 上任意一个。

# 代码模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

2022.04.11

posted @ 2022-08-22 14:08  Ethan'Chen  阅读(63)  评论(0)    收藏  举报