2022江苏省赛题解与代码(ABCDFGHIJKL)
和两个学弟一起vp的（有一个vp1小时就跑了，我是上完雅思开始了1小时才来打），还有一支同年级的队伍也参与了训练。总体来说题目质量还是不错的，江浙一带省赛竞争还是很激烈的（金牌线是6题1006罚时）
A、I、K
过于简单的签到题，不予赘述（PS：A题一定要认真读题目）
C
显然有调和级数复杂度的枚举倍数的转移，对于最长跳跃距离，我们很自然的想到用单调队列去维护。
贴一个学弟的代码:
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cstring>
#define int long long
#define inf 10000000000000000
#define M 1000005
using namespace std;
int n, q, p, a[M], f[M], s[M], st[M], ans[M];
bool t[M];
inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {
int x = 0; char c; bool f = false;
while(!isdigit(c = getchar())) if (c == '-') f = true;
do { x = (x << 1) + (x << 3) + (c ^ 48); }while(isdigit(c = getchar()));
if (f) return -x; return x;
}
WWW main() {
// freopen("a.in", "r", stdin), freopen("a.out", "w", stdout);
n = read(), q = read(), p = read();
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= q; i++) s[i] = read(), t[s[i]] = 1;
for (int d = 1; d <= p; d++) {
if (!t[d]) continue;
int l = 1, r = 0;
st[++r] = 0;
ans[d] = -inf;
for (int i = d; i <= n; i += d) {
while(l <= r and i - st[l] > p) l++;
f[i] = f[st[l]] + a[i];
while(l <= r and f[i] > f[st[r]]) r--;
st[++r] = i;
if (i + p >= n) ans[d] = Max(ans[d], f[i]);
}
}
for (int i = 1; i <= q; i++) {
if (s[i] > p) puts("Noob");
else printf("%lld\n", ans[s[i]]);
}
}
J
这道题目肯定会有人上来写记忆化搜索，显然的，我们记录 \(f(x)\) 为大小为x的超级平衡树的数量，在奇数情况下有 \(f(x) = f^2(\frac{x-1}{2})\)，在偶数情况下有 \(f(x) = 2f(\frac{x}{2})f(\frac{x - 2}{2})\)。容易发现，\(f(x)\) 的取值是2的幂，所以我们可以取对数来维护，记 \(F(x)=log_{2}(f(x))\)，由于模数是自然溢出，所以只要在 \(63 \leq F(x)\) 时，答案就是0了。
可是这道题卡了空间和时间，于是我们不能用记忆化搜索。但是我们发现搜索的每层本质不同的节点只有两个，而且大小只相差1，于是我们只需要维护他们的系数就可以递推了。
粘一个官方公式（不是我懒）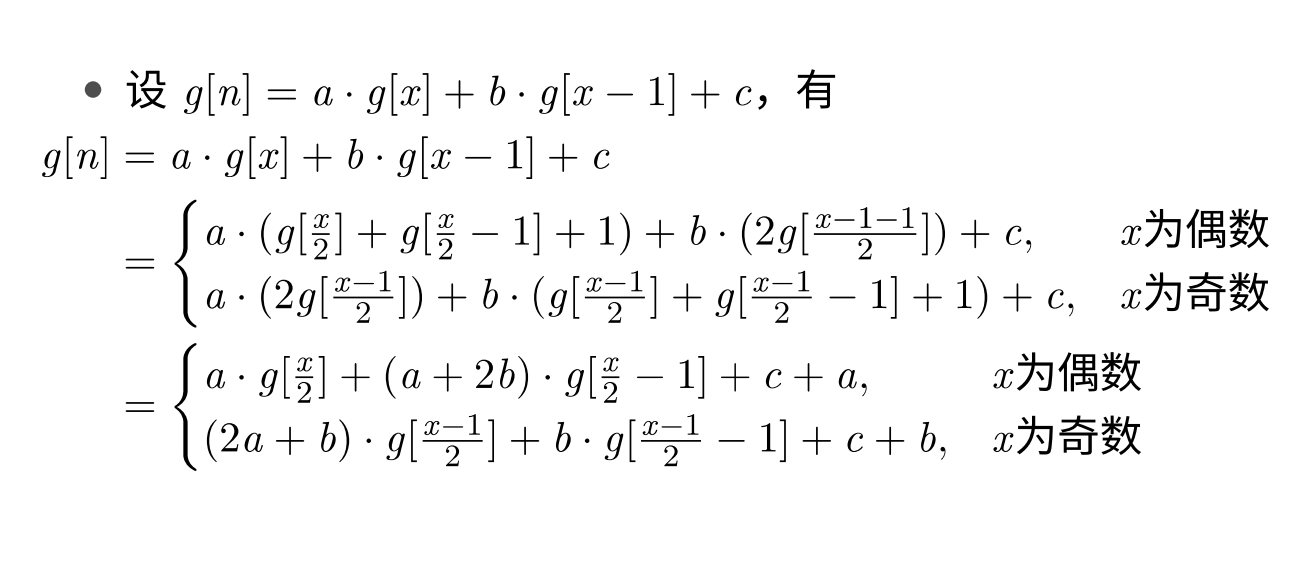
代码：
int T; ull n;
unordered_map <ull, ull> f, F, ANS , vis;
inline ull qpow(ull a, ull b) {
ull ret = 1;
for (; b; b >>= 1, a = a * a)
if (b & 1) ret = ret * a;
return ret;
}
inline ull dp(ull x) {
if (F.find(x) != F.end()) return F[x];
if (x & 1) return F[x] = 2ull * dp(x - 1 >> 1);
return F[x] = 1ull + dp(x >> 1) + dp((x >> 1) - 1ull);
}
signed main(void) {
for (read(T); T; T--) {
read(n); ull a, b, c;
a = 1; b = 0; c = 0;
while (n > 1) {
if (n & 1ull) {
c = c + b;
a = 2ull * a + b;
} else {
c = c + a;
b = 2ull * b + a;
}
if (c >= 64) break;
n >>= 1;
}
if (c >= 64) puts("0");
else writeln(qpow(2ull, c));
}
// fwrite(pf, 1, o1 - pf, stdout);
return 0;
}
L
一个不需要啥算法知识的妙妙思维题。我们考虑对于一个"ABC"来说，当我选择删B时，就不能在继续删这对了。而我删完AC后，就算还能前后接上新的AC，他们的奇偶性也会改变。所以这道题的本质是维护一个"ABC"前面有多少个能删B的串（即可以改变奇偶性）。显而易见的当前面能改变奇偶性或者我一开始的位置就能删B或者我这个串的合法能删次数大于1个时，一定能给后面贡献一次奇偶性的改变。那么我就可以知道一个串最多能删几次了。
代码：
int main() {
scanf("%s",s + 1);
n = strlen(s + 1); int cnt = 0, ans = 0;
for (int i = 2; i < n; i++) {
if (s[i] != 'B') continue;
int len = 0;
while (i - len - 1 >= 1 && i + len + 1 <= n && s[i - len - 1] == 'A' && s[i + len + 1] == 'C') ++len;
if (len == 0) continue;
ans += min(len - 1, (i % 2 == 0 ? 1 : 0) + cnt) + 1;
if (cnt || i % 2 || len > 1) cnt++;
}
cout << ans << '\n';
return 0;
}
B
听说是原题（CF510E），反正很典就是了。去年成都区域赛上也有一个数论背景的题目用网络流做的，当时时间不够没让我写，还是很遗憾的。
这个环一定长度是偶数的。因为除了2以外的所有质数都是奇数，而我们要把1~n放入若干个环里面，显然只能奇偶交替着来。我们考虑一个二分图，左边的点是所有奇数，右边是所有偶数。如果一个奇数和一个偶数的和是质数，那么就从这个奇数向偶数连一条容量为1的边。然后我们从源点向每个奇数连一条容量为2的边，再从每个偶数向汇点连一条容量为2的边。这样合法判定条件就是最大流得能流满每条连向汇点的边。我们可以dfs判断哪些边流满了来找出具体方案。
然后这个点数是 \(n = 1000\) ，经过计算我们发现边数的上界是 \(10981400\) ，讲道理求最大流肯定会超时口牙！
其实不然 https://www.cnblogs.com/searchstar/p/18437498 这篇博客说明了：
代码：
const int INF = 1 << 29;
const int Maxn = 1e4 + 5, Maxm = 10981410;
bool np[Maxn * 2]; int pp = 0;
inline void init() {
np[1] = true;
for (int i = 2; i <= int(2e4); i++) {
if (np[i]) continue; ++pp;
for (int j = 2; i * j <= int(2e4); j++) np[i * j] = true;
}
}
int n, m, s, t, cnt = 1, head[Maxn], cur[Maxn], ver[Maxm], nxt[Maxm], edge[Maxm];
inline void AddEdge(int u, int v, int w) {
ver[++cnt] = v, edge[cnt] = w, nxt[cnt] = head[u], head[u] = cnt;
ver[++cnt] = u, edge[cnt] = 0, nxt[cnt] = head[v], head[v] = cnt;
}
ll maxflow = 0; int dis[Maxn];
inline bool bfs(void) {
Ms(dis, 0); dis[s] = 1;
queue <int> q; q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = head[u]; i; i = nxt[i]) {
if (edge[i] && !dis[ver[i]]) {
q.push(ver[i]);
dis[ver[i]] = dis[u] + 1;
if (ver[i] == t) return true;
}
}
} return false;
}
inline int dinic(int u, int flow) {
if (u == t) return flow;
int rest = flow, k;
for (int &i = cur[u]; i; i = nxt[i]) {
if (edge[i] && dis[ver[i]] == dis[u] + 1) {
k = dinic(ver[i], min(rest, edge[i]));
if (!k) dis[ver[i]] = 0;
edge[i] -= k, edge[i ^ 1] += k;
rest -= k; if (rest == 0) break;
}
} return flow - rest;
}
bool inc[Maxn]; vector <int> ans[Maxn]; int cans = 0;
inline void dfs(int u, int f) {
if (f == -1) ans[++cans].push_back(u);
else ans[cans].push_back(u); inc[u] = true;
for (int i = head[u]; i; i = nxt[i]) {
if (ver[i] == f || ver[i] == s || ver[i] == t || inc[ver[i]]) continue;
if (u & 1) {
if (edge[i] == 0) {
dfs(ver[i], u); return;
}
} else {
if (edge[i] == 1){
dfs(ver[i], u); return;
}
}
}
}
signed main(void) {
read(n); s = n + 1; t = s + 1; init();
for (int i = 1; i <= n; i++)
if (i & 1) AddEdge(s, i, 2);
else AddEdge(i, t, 2);
for (int u = 1; u <= n; u += 2)
for (int v = 2; v <= n; v += 2)
if (!np[u + v]) AddEdge(u, v, 1);
while (bfs()) {
for (int i = 1; i <= n + 2; i++) cur[i] = head[i];
maxflow += dinic(s, INF);
}
if (maxflow != n) { puts("-1"); return 0; }
for (int i = 1; i <= n; i++) if (!inc[i]) dfs(i, -1);
writeln(cans);
for (int i = 1; i <= cans; i++) {
writeln(ans[i].size(), ' ');
for (int j = 0; j < ans[i].size(); j++) writeln(ans[i][j], " \n"[j == ans[i].size() - 1]);
}
// fwrite(pf, 1, o1 - pf, stdout);
return 0;
}
/**/
G
G这道题我真的一眼丁真出大于30之后只能是 \(\min(n,m) \leq S_p + 1\) 才有解，但是30以内的爆搜写TLE了，也是很难绷。
如果我们不用隔离方法（即把1和所有质数放一边，所有合数放一边），那么对于一个质数 \(p\) 来说只能把一个含 \(p\) 的数放一边，其他的数放另一边。我们先考虑最小的三个质数2、3、5，他们的最小公倍数是30。两两之间的公倍数有6、10、15 。那这四个数任意有两个在一边都会导致一个质数不合法，所以有30之后只能是把所有质数放一边。
对于小数据，我们可以搜索。一个显而易见的剪枝是在过程中不合法就直接return。但是如何判断合法性呢？每加一个数到一边时，我们可以遍历它有的质因子，检查当前质因子在两边集合的出现次数是不是都大于1了，如果是，那就非法了。
代码：
const int Maxn = 2e5 + 5;
bool np[Maxn]; int pp = 0, p[Maxn], cp[Maxn]; vector <int> sp[31];
inline void init() {
np[1] = false; p[++pp] = 1;cp[1]=1;
for (int i = 2; i <= int(2e5); i++) {
cp[i] = pp; if (np[i]) continue; p[++pp] = i; cp[i]++;
for (int j = 1; i * j <= 30; j++) sp[i * j].push_back(i);
for (int j = 2; i * j <= int(2e5); j++) np[i * j] = true;
}
}
int T, n, m, s, k; bool v[Maxn]; vector <int> an, am;
int cnt[31][2], a[31];
inline bool dfs(int dep, int d) {
if (dep > n + m) {
if (d == n) an.assign(a + 1, a + n + 1);
return d == n;
}
vector <int> &tp = sp[dep];
if (d < n) {
bool f = true;
for (auto i : tp) {
cnt[i][0]++;
if (cnt[i][0] > 1 && cnt[i][1] > 1) f = false;
}
if (f) {
a[d + 1] = dep;
if (dfs(dep + 1, d + 1)) return true;
}
for (auto i : tp) --cnt[i][0];
}
if (dep - d <= m) {
bool f = true;
for (auto i : tp) {
cnt[i][1]++;
if (cnt[i][0] > 1 && cnt[i][1] > 1) f = false;
}
if (f) {
if (dfs(dep + 1, d)) return true;
}
for (auto i : tp) --cnt[i][1];
}
return false;
}
signed main(void) {
init();
for (read(T); T; T--) {
read(n), read(m); an.clear(); am.clear();
for (int i = 1; i <= n + m; i++) v[i] = false;
s = min(n, m), k = n + m;
if (s <= cp[k]) {
puts("YES");
for (int i = 1; i <= s; i++) an.push_back(p[i]), v[p[i]] = true;
for (int i = 1; i <= k; i++) if (!v[i]) am.push_back(i);
if (n > m) swap(an, am);
for (int i = 0; i < an.size(); i++) writeln(an[i], " \n"[i == an.size() - 1]);
for (int i = 0; i < am.size(); i++) writeln(am[i], " \n"[i == am.size() - 1]);
continue;
}
if (n + m >= 30) { puts("NO"); continue; }
for (int i = 1; i <= 30; i++) cnt[i][0] = cnt[i][1] = 0;
if (dfs(1, 0)) {
for (int i = 1; i <= n; i++) v[an[i - 1]] = true;
for (int i = 1; i <= n + m; i++) if (!v[i]) am.push_back(i);
puts("YES");
for (int i = 0; i < an.size(); i++) writeln(an[i], " \n"[i == an.size() - 1]);
for (int i = 0; i < am.size(); i++) writeln(am[i], " \n"[i == am.size() - 1]);
} else puts("NO");
}
// fwrite(pf, 1, o1 - pf, stdout);
return 0;
}
F
● 考虑一次购买的生成函数
\[f(x) = \sum_{i} v_{i} x^{w_{i}}
\]
► 考虑答案就是
\[\sum_{i = 0}^{m} \sum_{j = 0}^{i + k} [x^{j}]f^{i}(x) = \sum_{i = 0}^{m} [x^{i + k}]f^{i}(x) \cdot \frac{1}{1 - x}
\]
● 定义生成函数变换式
\[g(x) = \frac{x}{f(x)}
\]
► 原式可表示为
\[[x^{m + k}] \frac{f^m(x)}{1 - x} \sum_{i=0}^{m} g^{m-i}(x)
\]
► 通过生成函数求和公式化简为
\[[x^{m + k}] \frac{f^m(x) \cdot (g^{m+1}(x) - 1)}{(1 - x)(g(x) - 1)}
\]
► 代入 \(g(x) = x/f(x)\) 进一步化简得
\[[x^{m + k}] \frac{x^{m+1} - f^{m+1}(x)}{(1 - x)(x - f(x))}
\]
你会发现我在搬运官方题解
这里有个注意点一半多项式快速幂时我们默认常数项是1，但是这个并不一定满足，所以得找到第一个非0项，先左移，再给每个系数乘上头部的乘法逆元，算完快速幂后再还原，然后右移。
代码：
const int mod = 998244353;
inline int qpow(int a, int b = mod - 2) {
int ret = 1;
for (; b; b >>= 1, a = 1ll * a * a % mod)
if (b & 1) ret = 1ll * ret * a % mod;
return ret;
}
const int Maxn = 8e5 + 5;
int invgen = qpow(3), rev[Maxn];
inline void NTT(int limit, int *arr, int type) {
for (int i = 0; i < limit; i++)
if (i < rev[i]) swap(arr[i], arr[rev[i]]);
for (int mid = 1; mid < limit; mid <<= 1) {
int w0 = qpow(type == 1 ? 3 : invgen, (mod - 1) / (mid << 1));
for (int i = 0; i < limit; i += mid << 1) { int w = 1;
for (int j = 0; j < mid; j++, w = 1ll * w * w0 % mod) {
int x = arr[i + j], y = 1ll * w * arr[i + j + mid] % mod;
arr[i + j] = (x + y) % mod; arr[i + j + mid] = (x - y + mod) % mod;
}
}
}
if (type == -1) {
int invlim = qpow(limit);
for (int i = 0; i < limit; i++) arr[i] = 1ll * arr[i] * invlim % mod;
}
}
inline void Times(int n, int *a, int *b, int *c) {
static int f[Maxn], g[Maxn];
int lim = 1; while (lim < n << 1) lim <<= 1;
for (int i = 0; i < lim; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? (lim >> 1) : 0), f[i] = a[i], g[i] = b[i];
NTT(lim, f, 1); NTT(lim, g, 1);
for (int i = 0; i < lim; i++) c[i] = 1ll * f[i] * g[i] % mod;
NTT(lim, c, -1);
}
inline void Inv(int length, int *a, int *b) {
if (length == 1) { b[0] = qpow(a[0]); return; }
Inv(length + 1 >> 1, a, b);
int lim = 1; while (lim < length << 1) lim <<= 1;
static int c[Maxn];
for (int i = 0; i < lim; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? (lim >> 1) : 0),
c[i] = i < length ? a[i] : 0;
NTT(lim, b, 1); NTT(lim, c, 1);
for (int i = 0; i < lim; i++) b[i] = 1ll * (2 - 1ll * c[i] * b[i] % mod + mod) % mod * b[i] % mod;
NTT(lim, b, -1); for (int i = length; i < lim; i++) b[i] = 0;
}
inline void Derivation(int length, int *a, int *b) {
for (int i = 1; i < length; i++) b[i - 1] = 1ll * i * a[i] % mod; b[length - 1] = 0;
}
inline void Integral(int length, int *a, int *b) {
for (int i = 1; i < length; i++) b[i] = 1ll * a[i - 1] * qpow(i) % mod; b[0] = 0;
}
inline void Getln(int length, int *a, int *b) {
static int g[Maxn], h[Maxn];
int lim = 1; while (lim < length << 1) lim <<= 1;
for (int i = 0; i < lim; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? (lim >> 1) : 0), g[i] = h[i] = 0;
Derivation(length, a, g); Inv(length, a, h);
NTT(lim, g, 1); NTT(lim, h, 1);
for (int i = 0; i < lim; i++) g[i] = 1ll * g[i] * h[i] % mod;
NTT(lim, g, -1); Integral(length, g, b);
}
inline void Getexp(int length, int *a, int *b) {
if (length == 1) return (void) (b[0] = 1);
Getexp(length + 1 >> 1, a, b);
static int bln[Maxn], c[Maxn]; Getln(length, b, bln);
int lim = 1; while (lim < length << 1) lim <<= 1;
for (int i = 0; i < lim; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? (lim >> 1) : 0),
c[i] = i < length ? (a[i] + (mod - bln[i])) % mod : 0;
c[0]++; NTT(lim, c, 1); NTT(lim, b, 1);
for (int i = 0; i < lim; i++) b[i] = 1ll * b[i] * c[i] % mod;
NTT(lim, b, -1); for (int i = length; i < lim; i++) b[i] = 0;
}
inline void Pow(int length, int *a, int k, int *b) {
static int f[Maxn], g[Maxn];
int lim = 1; while (lim < length << 1) lim <<= 1;
int h = -1;
for (int i = 0; i < length; i++) if (a[i] != 0) { h = i; break; }
if (h == -1) { for (int i = 0; i < length; i++) b[i] = 0; return; }
int ih = qpow(a[h], mod - 2), hk = qpow(a[h], k);
for (int i = 0; i < lim; i++) {
f[i] = g[i] = 0; if (i < length - h) f[i] = 1ll * a[i + h] * ih % mod;
}
Getln(length, f, g);
for (int i = 0; i < length; i++) g[i] = 1ll * g[i] * k % mod, f[i] = 0;
Getexp(length, g, f);
int hd = min(1ll * h * k, 1ll * length);
for(int i = length - 1; i >= hd; i--)
f[i] = 1ll * f[i - 1ll * h * k] * hk % mod;
for (int i = 0; i < hd; i++) f[i] = 0;
for (int i = 0; i < length; i++) b[i] = f[i];
}
int n, m, k, f[Maxn], g[Maxn], h[Maxn], F[Maxn];
signed main(void) {
read(n), read(m), read(k);
for (int i = 1, v, w; i <= n; i++) {
read(v), read(w); f[w] = (f[w] + v) % mod;
}
Pow(m + k + 1, f, m + 1, F);
for (int i = 0; i <= m + k; i++) F[i] = mod - F[i]; F[m + 1]++;
for (int i = 0; i <= m + k; i++) {
g[i] = -f[i];
if (i) g[i] += f[i - 1];
if (g[i] < 0) g[i] += mod;
if (g[i] >= mod) g[i] -= mod;
}
++g[1]; --g[2]; if (g[2] < 0) g[2] += mod;
Inv(m + k + 1, g, h);
for (int i = 0; i <= m + k; i++) f[i] = 0;
Times(m + k + 1, h, F, f);
writeln(f[m + k]);
//fwrite(pf, 1, o1 - pf, stdout);
return 0;
}
D、H
未完待续
浙公网安备 33010602011771号