应用拓扑讲义整理 Chapter 2. 图的拓扑

2.1 基本概念

2.1.1 图的表示

Definition 2.1（图）图是一个二元组 \((N,E)\)，其中 \(N\) 是顶点集，\(E\) 是边集，每条边是两个不同顶点的无序对。

Definition 2.2（有限和无限图）有限图是顶点有限的图，无限图是顶点可数无限多但每个顶点所连接的边都有限的图。

Definition 2.3（图的表示）图 \(G\) 的表示，记为 \(|G|\) ，是一个欧氏空间的子集。包括两个部分：

• 一个点集 \(|N|\)，每个顶点用一个点表示；
• 一个起点和终点都在 \(|N|\) 中的无交开曲线集 \(|E|\)，每条边用一条开曲线表示。

Theorem 2.4 每个有限图都可以在 \(\mathbb{R}^3\) 中表示。

Proof：只需证明有限的完全图都可以在 \(\mathbb{R}^3\) 中表示。容易在 \(\mathbb{R}^3\) 中取出 \(N_V\) 个不存在四点共面的点。这些点两两用直线段连接是互不相交的，因此得到了完全图的表示。任何有限图都是完全图的子集，因此也可以表示。

Exercise 2.5 下面是 Theorem 2.4 的一个错误证明。

• 在 \(\mathbb{R}^3\) 中取出两个点，用一条连续开曲线 \(\gamma\) 连接，将 \(\gamma\) 从 \(\mathbb{R}^3\) 中删去。
• 在 \(\mathbb{R}^3\backslash \gamma\) 中取出一个点，将每一对点都用连续开曲线连接。若有两条开曲线相交，则将曲线移动充分小的距离 \(\delta>0\) 使得它们不相交。
• 重复上述操作，则这些不相交的开曲线和它们的端点形成了图的一个表示。

Proof：未对曲线进行限定。曲线 \(\gamma\) 可能填满一个平面（Hilbert's Curve）导致无法通过移动充分小的距离来避免相交。

Definition 2.6（路径）图上的路径 \(P\) 是形如

\[N(P) = \{v_0,v_1,\dots,v_l\}\\ E(P) = \{v_0v_1,v_1v_2,\dots,v_{l-1}v_l\} \]

的集合。有时在不引起混淆的情况下，也将 \(N(P)\) 和 \(E(P)\) 简写为 \(N_P,E_P\)，甚至 \(N,E\)。

Definition 2.7（圈）图上的圈形如 \(P + v_0v_l\)。其中 \(P\) 是路径且 \(l\geq 2\)。

Definition 2.8（连通）图是连通（边-连通）的，如果任意两点间都有路径。

Theorem 2.9 图是连通的当且仅当它的表示 \(|G|\) 是道路连通的。

Definition 2.10（同源）称图中的两个顶点是同源的如果它们之间存在一条路径。

Theorem 2.11 同源是等价关系。

Definition 2.12（连通分量）同源等价类是连通分量。

Theorem 2.13 对任意图 \(G\)，其连通分量的数量等于 \(|G|\) 的道路连通分量的数量。

2.1.2 欧拉特征量

Definition 2.14（欧拉特征量） 图 \(G\) 的欧拉特征量定义为

\[\chi(G) = \#N_G - \#E_G. \]

Lemma 2.15 若图的表示是一条简单曲线，则它是 \(n\geq 1\) 条首尾相连的边。

Definition 2.16（树）树是不存在圈的图。根节点可以是树的任意一个顶点，叶节点是除根节点外的只连接一条边的点。

Theorem 2.17 任意一棵树都满足 \(\chi(T) = 1\)。

Proof：删去一个叶节点和它连接的边不改变图的欧拉特征量。可以递归证明一棵树可通过上述步骤删到仅有一个顶点。

Corollary 2.18 若一张图由 \(n\) 棵不交的树组成，则 \(\chi(G) = n\)。

Corollary 2.19 连通图满足 \(\chi(G) \leq 1\)。

Lemma 2.20 任意连通图中都存在包含所有顶点的子图，且是一棵树。

Proof：若 \(G\) 不存在圈，则由 Definition 2.16，结论已经成立。否则选择一个圈并从 \(E_G\) 中删去一条圈上的边，此时圈的数量减少。此时 \(G\) 仍然连通。重复上述步骤直到 \(G\) 不存在圈。

Definition 2.21（平面图）平面图是可以在欧氏平面上表示的图。

Theorem 2.22（约当曲线定理）平面上简单闭曲线的补集有两个道路连通分量，且其中一个有界，一个无界。

Lemma 2.23 若一条简单闭曲线是一张图的表示，则它是一个包含 \(n\geq 3\) 条首尾相连的边的圈。

Definition 2.24（洞）平面图 \(G\) 的洞是一个对应 \(\mathbb{R}^2\backslash G\) 的边界的圈。

Lemma 2.25 \(n\) 个顶点的连通平面图满足 \(\chi(G) = 1-n\)。

Definition 2.26（凸多面体） 凸多面体是欧氏空间中有限个点生成的凸集。

Definition 2.27（多面体）多面体是欧氏空间中具有平面多边形的面、直线段的边和尖角顶点的集合。满足

• 在 \(\mathbb{R}^3\) 中道路连通；
• 表面能被任意一个环切割成两部分。

Definition 2.28 多面体 \(P\) 的欧拉特征量定义为

\[\chi(P) = \#N - \#E + \#F. \]

2.1.3 Euler-Poincare 公式

Theorem 2.29（Euler Poincare 公式）任意多面体满足 \(\chi(P) = 2\)。

Proof：根据 Lemma 2.20，存在一棵树 \(T\) 包含所有顶点。构造 \(T\) 的对偶图 \(G\) 使得

• \(N_G\) 是 \(P\) 的每个面的中心
• \(P\) 所有不在 \(T\) 中的边对应 \(E_G\) 中连接其相邻面的中心的一条边。

可以证明 \(G\) 也是一棵树。因此

\[\chi(P) = \#N_T - (\#E_T + \#E_G) + \#E_G = \#N_T - \#E_T + \#N_G - \#E_G = 1+1 = 2. \]

Exercise 2.30 补充 Theorem 2.29 的证明。即证明 \(G\) 也是一棵树。

Proof：若 \(G\) 中有一个圈，则根据多面体的定义，这个圈将多面体分割为无交的两部分。根据 \(G\) 的构造方式，两部分之间的所有边都不在 \(T\) 中，即 \(T\) 不连通。矛盾。因此 \(G\) 也是一棵树。

Exercise 2.31 Theorem 2.17 的逆命题是否成立？

Proof：不成立。考虑 \(G = (N,E), N = \{v_1,v_2,v_3,v_4\}, E = \{v_1v_2,v_2v_3,v_1v_3\}\)，则 \(\chi(G)=1\) 但 \(G\) 有环 \(v_1v_2v_3\)。

Definition 2.32（正多面体）正多面体是所有边长度相等，所有面边数相等，所有点邻边数相等的多面体。

Definition 2.33（柏拉图立体）柏拉图立体是正四面体、正六面体、正八面体、正十二面体和正二十面体。

Exercise 2.34 证明：柏拉图立体是仅有的正多面体。

Proof：

2.1.4 自由阿贝尔群

Definition 2.35（线性独立）对阿贝尔群 \(G\)，一组元素 \(\{g_j\}_{j\in J}\) 线性无关如果

\[\sum_{j\in J}m_jg_j = 0, m_j\in \mathbb{Z}\Rightarrow \forall j\in J, m_j=0. \]

Definition 2.36（生成）对阿贝尔群 \(G\)，称一组元素 \(\{g_j\}_{j\in J}\) 生成 \(G\) 如果

\[\forall h\in G, \exists \{m_j\in \mathbb{Z}\},\text{s.t.}h=\sum_{j\in J} m_jg_j. \]

其中 \(m_j\) 是有限数。此时称 \(\{g_j\}_{j\in J}\) 为 \(G\) 的生成集。

Definition 2.37（基）称 \(\{g_j\}_{j\in J}\subset G\) 是阿贝尔群 \(G\) 的一组基，如果

\[\forall h\in G, \exists! \{m_j\in \mathbb{Z}\}_{j\in J},\text{s.t.}h=\sum_{j\in J}m_jg_j. \]

其中 \(m_j\) 是有限数。

Example 2.38 群 \(\mathbb{Z}_2\) 不存在一组基。假设它存在，则 \(1\) 不在基中因为 \(0 = 1+1 = 0\cdot 1\)，与唯一性矛盾。

Exercise 2.39 证明全体有理数构成的群不存在一组基。

Proof：假设基存在，若基中只有一个元素 \(\{a\}\)，则 \(\frac a2\in \mathbb{Q}\) 但不能由 \(\{a\}\) 生成。因此基中至少有两个元素。

假设 \(\frac mp, \frac nq\in B\)，其中 \((m,p)=(n,q)=1\)，令 \(N = mn\)，则 \(N = np\frac mp = mq\frac np\)，与唯一性矛盾。因此基不存在。

Theorem 2.40 \(\{g_j\}_{j\in J}\subset G\) 是阿贝尔群 \(G\) 的基当且仅当它线性无关且生成 \(G\)。

Proof：设 \(\{g_j\}_{j\in J}\subset G\) 是一组基，则根据定义，它生成 \(G\)。单位元 \(0\) 的分解是 \(\sum 0g_j= 0\)，假设存在另一组单位元分解，则 \(\sum_j m_jg_j=0\) 且至少有一个 \(m_j\) 非零。这与唯一性矛盾。因此 \(\{g_j\}\) 线性无关。

反之，设 \(\{g_j\}_{j\in J}\) 生成 \(G\)，则对所有 \(h\in G\)，有 \(h = \sum_j m_jg_j\)，其中 \(m_j\in \mathbb{Z}\)。假设存在另一组 \(n_j\in \mathbb{Z}\) 使得 \(h = \sum_j n_jg_j\)，则有 \(\sum_{j\in J} (m_j-n_j)g_j = 0\)。再由 \(\{g_j\}_{j\in J}\) 的线性无关性可得 \(m_j = n_j, \forall j\)。

Definition 2.41（自由阿贝尔群）自由阿贝尔群是存在一组基的阿贝尔群。

Corollary 2.42 在自由阿贝尔群中，单位元不在基中。

Proof：否则元素的分解将不唯一。

Definition 2.43（有限生成自由阿贝尔群）由有限集 \(S = \{s_1,s_2,\dots,s_n\}\) 生成的自由阿贝尔群是 \(\mathbb{Z}^S = \{f: S\rightarrow \mathbb{Z}\}\)，其加法定义为

\[\forall i = 1,2,\dots,n, (f+g)(s_i) := f(s_i) + g(s_i). \]

Corollary 2.44 设 \(S\) 是有限集。定义 \(\hat{s_i}: S\rightarrow \mathbb{Z}, s_i\in S\) 为

\[\hat{s_i}(s_j) := \begin{cases} 1, & i=j; \\ 0, & i\neq j. \end{cases} \]

则集合 \(\{\hat{s_i}: s_i\in S\}\) 是 \(\mathbb{Z}^S\) 的一组基，称为典范基底。

Proof：\(\mathbb{Z}^S\) 中的每个元素可表示为

\[f = \sum_{i=1}^n f(s_i)\hat{s_i}. \]

这些函数线性无关。

Definition 2.45（无限集生成的自由阿贝尔群）由可能无限的集合 \(S\) 生成的自由阿贝尔群是 \(\mathbb{Z}^S\) 的一个子群 \(\mathbb{Z}(S)\)，其包括所有函数 \(f: S\rightarrow \mathbb{Z}\)，满足 \(f(s) = 0\) 对除有限个之外的所有 \(s\in S\) 成立。

Corollary 2.46 \(\mathbb{Z}(S)\) 由 \(\{\hat{s_i}: s_i\in S, f(s_i)\neq 0\}\) 有限生成。

Definition 2.47（子群的和）两个子群 \(A,B\subset G\) 的和定义为

\[A+B := \{c\in G: \exists a\in A, b\in B, \text{s.t.} c=a+b\}. \]

Definition 2.48（子群的直和）称群 \(G\) 是它的两个子群 \(A\) 与 \(B\) 的直和如果

• \(G = A+B\)；
• 分解 \(c=a+b, c\in G\) 是唯一的。

Lemma 2.49 假设 \(G = A+B\)。则 \(G=A\oplus B\) 当且仅当 \(A\cap B = \{0\}\)。

Proof：充分性：假设 \(c = a_1+b_1 = a_2+b_2\) 是 \(c\in G\) 的两个分解。则

\[a_1-a_2 = b_2-b_1 \in A\cap B = \{0\}, \]

即两个分解是相同的。因此分解唯一。

必要性：任意 \(c\neq 0\) 不可能属于 \(A\cap B\) 因为 \(c = c+0\) 和 \(c=0+c\) 将是两个不同的分解。

Corollary 2.50 假设 \((G_i)_{i=1}^n\) 是 \(G\) 的一列子群，则 \(G = \oplus_{i=1}^n G_i\) 当且仅当

• \(G = \sum_{i=1}^n G_i\)；
• \(G_i\cap G_j = \{0\}, \forall i\neq j\)。

Corollary 2.51 若 \(\{g_1,g_2,\dots,g_n\}\) 是有限生成阿贝尔群 \(G\) 的一组基，则

\[G = \mathbb{Z}g_1\oplus \mathbb{Z}g_2\oplus\dots\oplus\mathbb{Z}g_n = \mathbb{Z}^n. \]

Proof：群的同构由 Definition 2.37 和 2.41 直接可得。

任意 \(h\in G\)，下证分解 \(h = \sum_{j=1}^n m_jg_j\) 是唯一的。

定义函数 \(\phi: G\rightarrow \mathbb{Z}^n\) 为

\[\phi(h) = (m_1,m_2,\dots,m_n). \]

因为 \(\phi(h_1-h_2) = (0,0,\dots,0)\Rightarrow h_1-h_2=0\)，所以 \(\phi\) 是单射；

因为 \(g_j\in G\)，所以 \(\{\phi(g_j)\}_{j\in J}\) 是 \(\mathbb{Z}^n\) 的典范基底，故生成 \(\mathbb{Z}^n\)，所以 \(\phi\) 是满射。

Lemma 2.52 设 \(G\) 是阿贝尔群。假设

\[\{g_j\}_{j\in J}\subset \{g_j\}_{j\in \overline{J}}\subset G \]

是群中元素的两个子集，前者生成 \(G\)，后者线性无关，则这两个子集相同。

Proof：假设结论不成立，即存在 \(j_0\in \overline{J}\backslash J\)。因为 \(\{g_j\}_{j\in J}\) 生成 \(G\)，所以存在集合 \(\{m_j\in \mathbb{Z}\}_{j\in J}\) 使得

\[g_{j_0} = \sum_{j\in J} m_jg_j. \]

即 \(-g_{j_0} + \sum_{j\in J}m_jg_j = 0\)，矛盾。

Corollary 2.53 阿贝尔群 \(G\) 的一组基同时是极大线性无关组和极小生成集。

Proof：从 \(B\) 中去除任意一个元素 \(g_0\) 会导致 \(g_0\) 无法被生成。另一方面，向 \(B\) 中加入任意一个元素 \(g_0\) 会导致线性无关性不成立。

Exercise 2.54 证明 Corollary 2.53 的逆命题不成立。

Proof：考虑群 \(G = \mathbb{Z}\oplus \mathbb{Z}_2\)。极大线性无关组是 \((1,0)\)，但基不存在；考虑有理数群 \(\mathbb{Q}\)。极小生成集是 \(\{\frac 1{2^n}\}\)，但基不存在。

Lemma 2.55 若 \(X = \{x_1,\dots,x_n\}\) 是自由阿贝尔群 \(G\) 的基，\(t\in \mathbb{Z}\)，则对任意 \(i\neq j\)，集合

\[Y = \{x_1,\dots,x_{j-1},x_j+tx_i,x_{j+1},\dots,x_r\} \]

也是 \(G\) 的一组基。

Proof：因为 \(X\) 生成 \(G\) 且 \(Y\) 生成 \(X\)，所以 \(Y\) 生成 \(G\)；又因为

\[\sum_{k=1}^n m_ky_k = 0\Rightarrow (m_i+m_jt)x_i + \sum_{k\neq i}m_kx_k=0, \]

所以 \(m_k=0\)。即 \(Y\) 线性无关。

Example 2.56 \(\{(0,1),(1,0)\}\) 和 \(\{(4,1),(1,0)\}\) 都是 \(\mathbb{Z}^2\) 的基，但 \(\{(0,4),(1,0)\}\) 不是。

Definition 2.57 设 \(G\) 和 \(H\) 是两个自由阿贝尔群，基分别为 \(\mathbf{v} = \{v_1,v_2,\dots,v_n\}\) 和 \(\mathbf{w} = \{w_1,w_2,\dots,w_n\}\)。称同构 \(\phi: G\rightarrow H\) 的矩阵为 \(B\in \mathbb{Z}^{n\times n}\)，满足

\[\forall v_j\in \mathbf{v}, \phi(v_j) = \sum_{i=1}^m b_{ij}w_i. \]

Exercise 2.58 利用 \(\mathbf{v},B,\mathbf{w}\) 表示元素 \(g\in G\) 和 \(\phi(g)\)。

Proof：设 \(g = \sum_{i=1}^n a_iv_i\)，则 \(\phi(g) = \sum_{i=1}^na_i\phi(v_i) = \sum_{i=1}^n\sum_{j=1}^m a_ib_{ij}w_j\)。

Definition 2.59（\(\mathbb{Z}\)-可逆）称整数矩阵 \(\mathbb{Z}-\)可逆如果它可逆且逆矩阵仍为整数矩阵。

Theorem 2.60 设 \(G\) 是非零自由阿贝尔群，秩为有限数 \(n\)，\(K\) 是 \(G\) 的非零子群。则 \(K\) 是秩为 \(s\leq n\) 的自由阿贝尔群。进一步地，存在一组 \(G\) 的基 \(\{x_1,x_2,\dots,x_n\}\) 和正整数 \(d_1,d_2,\dots,d_s\)，其中 \(d_i|d_{i+1}, i=1,\dots,s-1\)，使得 \(\{d_1x_1,d_2x_2,\dots,d_sx_s\}\) 是 \(K\) 的基。

2.1.5 有限生成阿贝尔群

Definition 2.61（有限生成阿贝尔群）有限生成阿贝尔群是具有一个有限生成集的阿贝尔群。

Theorem 2.62 任意两个有限生成自由阿贝尔群 \(G\) 的基是有限且有同样多元素的。

Proof：设 \(G\) 有基 \(\{g_j\}_{j\in J}\) 且由 \(h_1,h_2,\dots,h_n\) 生成。由 Definition 2.37 有

\[\forall i = 1,\dots,n, h_i = \sum_{j\in J} m_{ij}g_j. \]

其中 \(J_i := \{j\in J: m_{ij}\neq 0\}\) 有限。即集合 \(\overline J := \cup_{j=1}^n J_i\) 有限且

\[\forall i = 1,\dots,n, h_i = \sum_{j\in J} m_{ij}g_j. \]

因此有

\[\forall h\in G, h = \sum_{i=1}^n k_ih_i = \sum_{i=1}^n k_i\sum_{j\in \overline J} m_{ij}g_j = \sum_{j\in J}(\sum_{i=1}^n k_im_{ij})g_j. \]

即基 \(\{g_j\}_{j\in \overline J}\) 生成了 \(G\) 且 \(\overline J\) 有限。\(J\) 不可无限否则将与 Corollary 2.53 矛盾。

另一方面，将 \(\{g_j\}_{j\in J}\) 重写为 \(g_1,g_2,\dots,g_n\)，则由 Corollary 2.51 有

\[\begin{aligned} G &=g_1\mathbb{Z}\oplus g_2\mathbb{Z}\oplus\dots\oplus g_n\mathbb{Z};\\ 2G &= 2g_1\mathbb{Z}\oplus 2g_2\mathbb{Z}\oplus\dots\oplus 2g_n\mathbb{Z}. \end{aligned} \]

因为直积的商群等于商群的直积，所以 \(G/2G = \mathbb{Z}_2^n, |G/2G| = 2^n\)，即 \(n = \log_2 |G/2G|\)。

因此自由阿贝尔群的元素个数与基的选择无关。

Definition 2.63（有限生成自由阿贝尔群的秩）有限生成自由阿贝尔群的秩是它（任意）的基的元素数量。

Theorem 2.64 任意有限生成阿贝尔群同构于

\[G = \mathbb{Z}_{m_1} \times \mathbb{Z}_{m_2}\times \dots\times \mathbb{Z}_{m_r}\times \mathbb{Z}^n, \]

其中 \(m_i | m_{i+1}, \forall i = 1,\dots,r-1\)。

Definition 2.65（Betti 数和挠系数）有限生成阿贝尔群 \(G\) 的 Betti 数定义为 \(\mathbb{Z}\) 的次数；\(G\) 的挠系数是整数 \(m_1,m_2,\dots,m_r\)。

Definition 2.66（有限生成阿贝尔群的秩）有限生成阿贝尔群 \(G\) 的秩是它的 Betti 数与挠系数之和。

Theorem 2.67（有限生成阿贝尔群基本定理）每个有限生成阿贝尔群都同构于

\[G = \mathbb{Z}_{p_1^{r_1}}\times \mathbb{Z}_{p_2^{r_2}}\times \dots\times \mathbb{Z}_{p_m^{r_m}}\times \mathbb{Z}^n. \]

其中 \(p_i\) 是素数（未必不同），\(r_1\) 是正整数。进一步地，直积在不考虑因子顺序交换的意义下是唯一的。即 \(p_i^{r_i}\) 和 \(n\) 唯一。

Definition 2.68（可分解）称群 \(G\) 是可分解的，如果它与自身的两个真子群的直积同构。否则称它不可分解。

Corollary 2.69 有限不可分解阿贝尔群只可能是阶数为素数幂次的循环群。

Corollary 2.70 若 \(m\) 整除有限阿贝尔群 \(G\) 的阶数，则 \(G\) 有阶数为 \(m\) 的子群。

Proof：由 Theorem 2.67 得

\[G = \mathbb{Z}_{p_1^{r_1}}\times \mathbb{Z}_{p_2^{r_2}}\times \dots\times \mathbb{Z}_{p_n^{r_n}}. \]

其中 \(p_i\) 不一定不同。因为 \(m\mid|G| = \prod_{i=1}^n p_i^{r_i}\)，所以 \(m = \prod_{i=1}^n p_i^{s_i}, 0\leq s_i\leq r_i\)。

因为循环群 \(\langle p_i^{r_i-s_i}\rangle\) 的阶数是 \(p_i^{s_i}\)，所以 \(\langle\prod_{i=1}^n(p_i)^{r_i-s_i}\rangle\) 是 \(G\) 阶为 \(m\) 的子群。

2.2 图的同调

2.2.1 顶点和边的链

Definition 2.71（点链和边链） 顶点或边的链是一列顶点或边的满足抵消律的形式和，即 \(x+x=0\)。特别地，边链中不能含有连续出现两次的同一条边（\(AA\)）或方向相反的边（即认为 \(AB=BA\)）。

Example 2.72 下图有三个环 \(a,b,c\)：

它们是线性相关的，因为

\[\begin{aligned} a &= 12 + 25 + 56 + 61 \\ b &= 23 + 34 + 45 + 52 \\ a+b &= 12 + 25 + 56 +61 + 23 + 34 + 45 + 52 \\ &= 12 + 23 + 34 + 45 + 56 + 61 = c. \end{aligned} \]

Definition 2.73（0-链群和1-链群）

点链的集合（0-链群）定义为

\[C_0(G) = \{\sum_{A\in Q} A: Q\subset N_G\}\cup \{0\}. \]

边链的集合（1-链群）定义为

\[C_1(G) = \{\sum_{AB\in P} AB: P\subset E_G\}\cup \{0\}. \]

不引起混淆时也将它们简写为 \(C_0,C_1\)。

Lemma 2.74 设 \(+\) 为满足抵消律的形式和。则 \((C_0(G),+)\) 和 \((C_1(G), +)\) 分别为 \(N_G\) 和 \(E_G\) 生成的阿贝尔群。即

\[C_0(G) = \langle N_G\rangle, \\ C_1(G) = \langle E_G\rangle. \\ \]

Lemma 2.75 \(C_0(G)\) 和 \(C_1(G)\) 都是域 \(\mathbb{Z}_2\) 上的线性空间。

Proof：设 \((G,+)\) 是满足 \(\forall x\in G, x+x=0\) 的群，则 \(G\) 可看作在域 \(\mathbb{Z}_2 = \{0,1\}\) 上的域，其中 \(+\) 是通常意义上的加法。数乘运算在这个定义下也是显然的。

2.2.2 边界算子

Definition 2.76（图的边界算子）图 \(G\) 的边界算子 \(\partial_G: C_1(G)\rightarrow C_0(G)\) 定义为

\[\begin{aligned} \forall AB \in E_G, \partial_G(AB) &= A+B, \\ \forall x,y\in E_G, \partial_G(x+y) &= \partial_G(x) + \partial_G(y). \end{aligned} \]

Lemma 2.77 边界算子 \(\partial_G\) 是群同态。

Lemma 2.78 边界算子 \(\partial_G\) 是 \(C_1(G)\) 到 \(C_0(G)\) 的线性映射。

Definition 2.79（1-环）称一条 1-链 是 1-环 如果它的边界为 0。图 \(G\) 的 1-环群定义为

\[Z_1(G) := \ker \partial_G = \{x\in C_1(G): \partial_Gx = 0\}, \]

不引起混淆时也将它简写为 \(Z_1\)。

Example 2.80 考虑下面的图结构

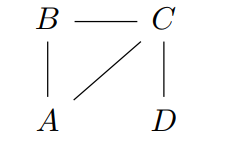
根据以上定义，有

\[\begin{aligned} C_0 &= \langle N_G\rangle = \langle\{A,B,C,D\}\rangle, \\ C_1 &= \langle E_G\rangle = \langle\{AB,BC,CA,CD\}\rangle. \\ \end{aligned} \]

若将 \(A,B,C,D\) 视为单位矩阵的 4 个列向量，\(AB,BC,CA,CD\) 同理，则 \(\partial(AB) = A+B\) 即

\[\partial([1,0,0,0]^T) = [1,1,0,0]^T, \]

这表明边界算子 \(\partial\) 的变换矩阵 \(M_\partial\) 的第一列是等式右端的向量。因此有

\[M_\partial = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \]

根据 \(M_\partial\) 的核空间可得

\[Z_1(G) = \ker\partial_G = \{0, AB+BC+CA\}. \]

且 \(\text{rank} Z_1 = 1\)。即 \(G\) 只有一个“洞”。

Exercise 2.81 对 Example 2.72 做类似 Example 2.80 的代数推导并得到 \(\text{rank}Z_1 = 2\).

Solution：

\[\begin{aligned} C_0 &= \langle\{1,2,3,4,5,6\}\rangle, \\ C_1 &= \langle\{12,16,23,25,34,45,56\}\rangle, \\ M_\partial &= \begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{aligned} \]

\(\ker M_\partial = \langle[1,1,0,1,0,0,1]^T,[0,0,1,1,1,1,0]^T\rangle\)，所以 \(\text{rank}Z_1 = 2\)，且

\[\ker M_\partial = \{0, 12+16+25+56, 23+25+34+45, 12+16+23+34+45+56\}. \]

Lemma 2.82 平面图的洞数等于其线性无关的环数，即等于边界算子的核空间的维数。

Definition 2.83（0-边界）称 0-链 是 0-边界 如果它是某个 1-链 的边界。图 \(G\) 的0-边界群是它的边界算子的像空间：

\[B_0(G) = \text{Im}\partial_G = \{P\in C_0(G): \exists w\in C_1(G), \text{s.t.} \partial w = P\}. \]

Lemma 2.84 0-边界群是 \(C_0\) 的子群。

Example 2.85 对 Example 2.80 中的图，有

\[B_0 = \langle\{A+B, B+C, C+A, C+D\}\rangle = \langle\{A+B,B+C,C+D\}\rangle. \]

因此 \(\text{rank}B_0 = 3\)。根据 Definition 2.14，Theorem 2.17 和 Lemma 2.20，\(\text{rank}C_0 - \text{rank} B_0 = 1\)可推至 \(G\) 只有一个连通分支：\(C_0\) 的生成元就是图的所有顶点，\(B_0\) 的生成元就是图的一些边。

2.2.3 商群同调

Definition 2.86（同调）称两个 0-链 \(P,Q\in C_0(G)\) 同调，记作 \(P\sim Q\)，如果存在 1-链 \(w\in C_1(G)\) 满足 \(\partial w = P+Q\)。

Definition 2.87（0-同调）图 \(G\) 的 0-同调群 是

\[H_0(G) = C_0(G)/B_0(G), \]

1-同调群是

\[H_1(G) = Z_1(G) = \ker\partial_G. \]

不引起混淆时也将它们简写作 \(H_0,H_1\)。

Definition 2.88（Betti 数）图 \(G\) 的 Betti 数是它的同调群的秩，即

\[\beta_i = \text{rank}H_i. \]

Lemma 2.89 有限生成阿贝尔群 \(L\) 和它的子群 \(M\) 满足

\[\text{rank}(L/M) = \text{rank}L-\text{rank}M. \]

Theorem 2.90 \(\beta_0 = \text{rank}C_0(G) - \text{rank Im}\partial_G\)。

Example 2.91 考虑下面的图

\[\begin{aligned} C_0 &= \langle\{A,B,C,D\}\rangle, \\ C_1 &= \langle\{AB,BC\}\rangle, \\ M_\partial &= \begin{bmatrix} 1 & 0 \\ 1 & 1 \\ 0 & 1 \\ 0 & 0 \\ \end{bmatrix} \end{aligned} \]

\(M_\partial\) 列是满秩的，所以 \(Z_1 = \ker\partial_G = \{0\}\)，即 \(G\) 中不存在环。

\(G\) 的边界群为

\[B_0 = \text{Im}\partial = \langle\{A+B,B+C\}\rangle = \{0,A+B,B+C,C+A\}. \]

且 \(\text{rank} B_0 = 2\)。因此其连通分支数为 \(\text{rank}(C_0) - \text{rank}(B_0) = 2\)。因此 \(C_0\) 可以划分为 \(B_0\) 的两个陪集：

\[\begin{aligned} \ [A] := A + B_0 &= \{A,B,A+B+C,C\} = [B] = [C], \\ \ [D] &= \{D,A+B+D,B+C+D,C+A+D\}, \\ \ [A+D] &= \{A+D,B+D,A+B+C+D,C+D\}. \\ \end{aligned} \]

Exercise 2.92 对 Example 2.72 做类似 2.91 的代数推导。

Solution：Exercise 2.81 已经计算出了 \(H_1 = Z_1 = \langle\{12+16+25+56, 23+25+34+45\}\rangle\)。因此 \(G\) 有两个线性无关的环。

\(G\) 的边界群为

\[B_0 = \text{Im}\partial = \langle\{1+2,1+6,2+3,2+5,3+4,4+5,5+6\}\rangle. \]

且 \(\text{rank}B_0 = 5 = N_G-1\)，因此 \(G\) 只有一个连通分支且 \(H_0 = \{[0],[1]\}\)。

Exercise 2.93 计算下列图的同调群。图中有 \(n\) 条边，排列为：（1）线形（2）环形（3）星形。

Solution：因为三种情况下 \(n\) 条边都是连通的，所以 \(H_0 = \{[0],[1]\}\)。

对（1）和（3），图中不存在环，所以 \(H_1 = \{0\}\)。

对（2），图中只有一个环即由全部点构成的环，所以 \(H_1 = \{0, 1+2+\dots+n\}\)。

Exercise 2.94 计算 \(n\times m\) 网格图的同调群。

Solution：设点标号为 \((0,0)\dots(n,n)\)。则

\(H_0 = \{[0],[(0,0)]\}\)；

\[\begin{aligned} H_1 = &\langle\{(i,j)(i,j+1), (i,j)(i+1,j),(i,j+1)(i+1,j+1),(i+1,j)(i+1,j+1) \\ &| 0\leq i,j<n\}\rangle. \end{aligned} \]

Exercise 2.95 若允许图中有自环但边没有定向，同调群和 Betti 数是否还有意义？

Solution：仍有意义。此时每个自环都是 \(H_1 = Z_1\) 的基中的一个元素。

2.3 图的映射

2.3.1 图映射

Definition 2.96（图映射）图映射是图之间的映射 \(f: G\rightarrow J\)：

\[f = \{f_N: N_G\rightarrow N_J, f_E: E_G\rightarrow E_J\cup N_J\} \]

其满足离散连续条件

\[f_E(AB) = \begin{cases} f_N(A)f_N(B), & f_N(A)\neq f_N(B); \\ f_N(A), & f_N(A) = f_N(B). \end{cases} \]

Example 2.97 下面是图映射的一个例子：

2.3.2 链映射

Definition 2.98 由图映射 \(f: G\rightarrow J\) 生成的链映射是一对同态 \(f_\Delta := \{f_0, f_1\}\)，

\[f_0: C_0(G)\rightarrow C_0(J);\quad f_1: C_1(G) \rightarrow C_1(J), \]

分别由 \(f_N\) 和 \(f_E\) 生成。

Theorem 2.99（代数连续条件）任意图映射 \(f: G\rightarrow J\) 生成的链映射满足

\[\forall c\in E_G, \quad \partial_Jf_1(e) = f_0(\partial_G e). \]

其一般也写作 \(\partial f = f\partial\)。可以用下面的交换图表示。

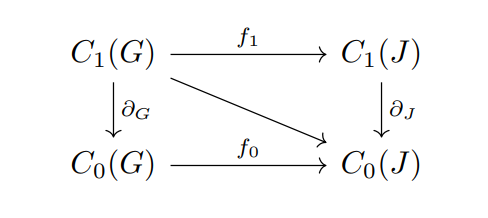
Proof：对一条边 \(e:=AB\in E_G\)，\(f_N(A) = f_N(B)\)，\(f_1(e) = 0\)，所以交换成立。否则有

\[\partial_Jf_1(AB) = \partial_J(f_N(A)f_N(B)) = f_N(A) + f_N(B) = f_0(A+B) = f_0(\partial_Ge). \]

故交换成立。

Example 2.100 对图映射 \(f: G\rightarrow J\)，若它粘连了所有的边，则其链映射 \(f_0\) 将同一个连通分支内的所有顶点映射到同一个顶点，\(f_1\) 则是平凡同态，即 \(f_1 = 0\)。

Example 2.101 下面两个链映射

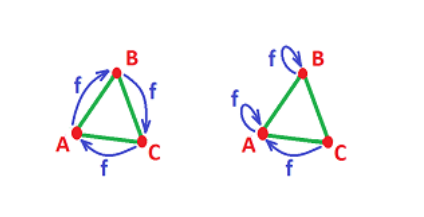
的矩阵分别为：

\[M_L = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{bmatrix} \]

和

\[M_R = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \]

Corollary 2.102 对链映射 \(f_\Delta = \{f_0,f_1\}\)，\(f_0\) 将边界映射到边界，\(f_1\) 将环映射到环。

Proof：由 Theorem 2.90，有

\[\begin{aligned} x = \partial_G(y) & \Rightarrow f_0(x) = f_0(\partial_G(y)) = \partial_J(f_1(y)); \\ \partial_G(y) = 0 & \Rightarrow \partial_J(f_1(y)) = f_0(\partial_G(y)) = f_0(0) = 0. \\ \end{aligned} \]

Exercise 2.103 由于离散连续条件，道路连通分支数是不能增加的。而相对的，图映射可以使环的数量增加、不变或减少。对所有情况给出一个例子。

Proof：考虑 \(G = (V,E), V = \{1,2,3\}, E = \{12,13,23\}\)。

减少：\(f_V(1) = f_V(2) = f_V(3) = 1, f_E(12) = f_E(23) = f_E(31) = 1\)，环的数量由 1 变为 0；

不变：\(f\) 为恒等映射；

再考虑 \(G = (V,E), V = \{1,2,3,4\}, E = \{12,23,34\}\)。

增加：\(f_V(1) = f_V(4) = 1, f_V(2) = 2, f_V(3) = 3\)，\(f_E(12) = 12, f_E(23) = 23, f_V(34) = 31\)，环的数量由 0 变成 1。

2.3.3 同调映射

Definition 2.104（环映射）环映射 \(f_{1z}: Z_1(G)\rightarrow Z_1(J)\) 是将 \(f_1\) 限制到 \(Z_1(G)\) 和 \(Z_1(J)\) 所得的映射。

Corollary 2.105 环映射是良定义的。

Proof：Corollary 2.102。

Example 2.106 Example 2.101 的 \(G\rightarrow G\) 的映射诱导的环映射是什么？

对旋转映射，有

\[\begin{aligned} Z_1(G) &= \langle AB+BC+CA\rangle \\ f_{1z}(AB+BC+CA) &= BC+CA+AB. \end{aligned} \]

因此 \(f_{1z}\) 就是恒等映射。

对右侧的映射，有

\[\begin{aligned} Z_1(G) &= \langle AB+BC+CA\rangle \\ f_{1z}(AB+BC+CA) &= AB+BA+0 = 0, \end{aligned} \]

因此 \(f_{1z}\) 就是平凡映射。

Lemma 2.107 考虑两个阿贝尔群 \(A,B\) 和它们之间的同态 \(F:A\rightarrow B\)。假设两个子群 \(A''\subset A'\subset A\) 和 \(B''\subset B'\subset B\) 满足

\[F(A')\subset B', F(A'') = B''. \]

则商映射 \([F]: A'/A''\rightarrow B'/B''\) 定义为

\[[F](0) = 0, \forall x\in A', [F]([x]) = [F(x)]. \]

Proof：Trivial。

Example 2.108 令 \(K = \mathbb{Z_2\times Z_2}\)。找到所有同态映射 \(f: K\rightarrow K\) 满足

\[[f]: K/\langle(1,1)\rangle \rightarrow K/\langle(1,0)\rangle \]

且良定义。

令 \(A = A' = B = B' = K\)，

\[A'' = \langle (1,1)\rangle = \{(0,0),(1,1)\}, \\ B'' = \langle (1,0)\rangle = \{(0,0),(1,0)\}, \\ \]

因为 \(f\) 是同态映射，所以 \(f(0,0) = (0,0)\)。

根据拉格朗日定理，\(A'\) 包含两个不同的 \(A''\) 的陪集。因此 \(f(1,1) = (0,0)\) 或 \(f(1,1) = (1,0)\)。

对陪集 \(A'' + (1,0) = \{(0,1),(1,0)\}\)，其像集 \(f\) 是 \(B''\) 或 \(B'' + (1,1)\)。

对 \(f(A'' + (1,0))\subset B''\)，有 4 种情况

\[(0,1)\mapsto (1,0), (1,0)\mapsto (1,0), \\ (0,1)\mapsto (0,0), (1,0)\mapsto (0,0), \\ (0,1)\mapsto (1,0), (1,0)\mapsto (0,0), \\ (0,1)\mapsto (0,0), (1,0)\mapsto (1,0), \\ \]

每种情况唯一确定了一个 \(f(1,1)\)。同理讨论 \(f(A'' + (1,0))\subset B'' + (1,1)\)，可得 8 种不同情况

映射 \(f: K\rightarrow K\) 的总数为 $ 4^4 = 256$，而满足条件的只有 \(8\) 种。

Exercise 2.109 将反射映射和旋转映射视作同态 \(f : \mathbb{R}^3\rightarrow \mathbb{R}^3\)。它们是否诱导了商群 \(\mathbb{R} = \mathbb{R^3 / R^2}\) 良定义的商映射？

Proof：

Corollary 2.110 令 \([z] := z + B_0(G)\) 定义为 0-cycle \(z\) 的陪集。则连通分量映射 \([f_0]: H_0(G)\rightarrow H_0(J)\) 是良定义的。

\[[f_0]([z]) = [f_0(z)]. \]

Proof：由 Corollary 2.102，\(f_0(B_0(G))\subset B_0(J)\)。由 Definition 2.98，\(f_0(C_0(G))\subset C_0(J)\)。因此由 Lemma 2.107 可得结论。

Example 2.111 考虑两个顶点的图 \(G\) 和一个顶点的图 \(J\)

\[N_G = N_J = \{A,B\}, E_G = \emptyset, E_J = \{AB\}. \]

则连通分量的合并可表示为图映射 \(f_N(A) = A, f_N(B) = B\)。因此有

\[\begin{aligned} C_0(G) &= H_0(G) = \langle [A], [B]\rangle; \\ C_0(J) &= C_0(G), H_0(J) = \langle [A] = [B]\rangle; \\ [f_0]([A]) &= [f_0]([B]) = [A]. \end{aligned} \]

Definition 2.112 图映射 \(f\) 的同调映射为一对映射 \(f_* = \{[f_0], f_{1z}\}\)。

Theorem 2.113 同调映射是保单位元、保复合和可逆的。即

\[\begin{aligned} ~[(\text{Id}_G)_0] = \text{Id}_{H_0(G)}&,\quad (\text{Id}_G)_{1z} = \text{Id}_{H_1(G)}; \\ [(fg)_0] = [f_0][g_0]&, \quad (fg)_{1z} = f_{1z}g_{1z}, \\ [(f^{-1})_0] = [f_0]^{-1}&, \quad (f^{-1})_{1z} = f_{1z}^{-1}. \end{aligned} \]

Exercise 2.114 令 \(\beta_0\) 和 \(\beta_1\) 是图 \(G\) 的前两个 Betti 数。考虑 \(G\) 上的图映射 \(f = (f_N, f_E)\)，\(f_E\) 是恒等映射。令 \(\beta_0'\) 和 \(\beta_1'\) 为 \(K = f(G)\) 的前两个 Betti 数，证明

\[\dim \ker f_N = (\beta_1' - \beta_1) - (\beta_0' - \beta_0). \]

并给出例子验证。

Proof：由第一同构定理得

\[\dim\ker f_N + \dim\text{Im} f_N = |N|, \]

因为 \(\dim \text{Im} f_N = |N'|\)，所以 \(\dim \ker f_N = |N| - |N'|\)。

因为 \(\beta_1 - \beta_0 = (|E| - |N| + \beta_0) - \beta_0 = |E| - |N|\)，同理 \(\beta_1' - \beta_0' = |E'| - |N'|\)，

所以 \((\beta_1' - \beta_1) - (\beta_0' - \beta_0) = |E'| - |E| + |N| - |N'| = |N| - |N'| = \dim\ker f_N\)。

例如 \(N = \{1,2,3\},E = \{12\}, f_N(1) = 2, f_N(2) = 1, f_N(3) = 1, f_E(12) = 12\)，

则 \(\dim \ker f_N = 1, \beta_1 = \beta_1' = 0, \beta_0 = 2, \beta_0' = 1\)。

2.4 图上的二元计算

2.4.1 群或空间的对偶

Definition 2.115（群的对偶）群 \((L,\cdot)\) 在 \(\mathbb{Z_2}\) 上的对偶，记为 \(L^*\)，是 \(L\) 上的全体群同态

\[L^* = \{s: L\rightarrow \mathbb{Z}_2 | s(xy) = s(x) + s(y)\}. \]

Lemma 2.116 \(\mathbb{Z}_2\) 的对偶群同构于 \(\mathbb{Z}_2\)。

Proof：所有同态 \(h\) 一定满足 \(h(0) = 0\)。因为 \(h(1) = 0\) 或 \(h(1) = 1\)，所以可定义

\[1^* = \{0\mapsto 0,1\mapsto 1\}, 0^* = \{0\mapsto 0, 1\mapsto 0\}, \]

即 \(h\) 为单位映射 \(1^*\) 或平凡映射 \(0^*\)。

考虑映射 \(f: \mathbb{Z_2\rightarrow Z_2^*}\)，\(f(x) = x^*\)。则容易验证

\[f(0+0) = f(0) = 0^* = 0^* + 0^*; \\ f(0+1) = f(1) = 1^* = 0^* + 1^*; \\ f(1+1) = f(0) = 0^* = 1^* + 1^*. \]

Lemma 2.117 \(\mathbb{Z}_2\) 的对偶也是环。

Proof：Trivial。

Theorem 2.118 群 \(L := (\mathbb{Z_2})^n\) 满足

\[L^* \cong L. \]

Proof：每个 \(x\in L\) 可写作 \(x = (x_1,\dots,x_n), x_i\in \mathbb{Z}_2\)。

它可以对应 \(L^*\) 中的元素 \(x^* = (x_1^*, \dots, x_n^*), x_i^* \in \mathbb{Z}_2^*\)。

Exercise 2.119 定义 \(n=3\) 时 \(\mathbb{Z}_n\) 在 \(\mathbb{Z}_2\) 上的对偶。对 \(n>3\)？

Proof：\(\mathbb{Z}_3\) 到 \(\mathbb{Z}_2\) 的同态有

\[0^* = \{0\mapsto 0, 1\mapsto 0, 2\mapsto 0\}, \\ 1^* = \{0\mapsto 0, 1\mapsto 1, 2\mapsto 0\}, \\ \]

且满足 \(x^* + y^* = (x+y)^*\)。因此 \(\mathbb{Z}_3^* \cong \mathbb{Z}_2\)。

同理也有 \(\mathbb{Z}_n \cong \mathbb{Z}_2\)。

2.4.2 点和边的反链

Definition 2.120（\(k\)-反链）图 \(G\) 的 \(k\)-反链是同态 \(s : C_k(G)\rightarrow \mathbb{Z}_2\)。

Lemma 2.121 图 \(G\) 上的 \(0\)-反链和 \(1\)-反链的集合，分别记为 \(C^0(G)\) 和 \(C^1(G)\)，分别是 \(C_0(G)\) 和 \(C_1(G)\) 的对偶群。

Definition 2.122（基本链和基本反链）群 \(G\) 的基本链是 \(G\) 的顶点或边；基本链 \(x\) 的基本反链 \(x^*: C_k\rightarrow \mathbb{Z}_2\) 定义为

\[\begin{cases} 1, \quad t = x, \\ 0, \quad t \neq x. \\ \end{cases} \]

Lemma 2.123 图 \(G\) 的\(0\)-反链群和 \(1\)-反链群分别可以表示为

\[\begin{aligned} C^0(G) &= \left\{\sum_{A\in Q}A^* : Q\subset N_G\right\}\cup \{0^*\}; \\ C^1(G) &= \left\{\sum_{AB\in P} AB^* : P\subset E_G\right\}\cup \{0^*\}, \\ \end{aligned} \]

其中 \(A^*\) 和 \(AB^*\) 是 Definition 2.122 的基本链。

Proof：由 Definition 2.120，\(s(x+y) = s(x) + s(y)\) 对 \(k\)-反链 \(s\) 成立。因此 \(s\) 在 \(k\)-链上的值完全由它在单个顶点或边上的值决定。

考虑在 \(Q\subset N_G\) 上赋值为 \(1\)，在 \(N_G\backslash Q\) 上赋值为 \(0\) 的 \(0\)-反链。则 \(0\)-反链可以表示为 \(\sum_{A\in Q} A^*\)：

\[\forall B\in Q, \left(\sum_{A\in Q} A^*\right)(B) = B^*(B) = 1, \forall C\not\in Q, \left(\sum_{A\in Q} A^*\right)(C) = 0. \]

特别地，将在所有点上赋值为 \(0\) 的反链称为 \(0^*\)，将在所有点上赋值为 \(1\) 的反链称为 \(1^*\)。

Lemma 2.124 \(C^k\) 是 \(C_k\) 的对偶空间。

Lemma 2.125 对任意图 \(G = (N,E)\)，有

\[C_0 \cong C^0 \cong (\mathbb{Z}_2)^n, \quad C_1 \cong C^1\cong (\mathbb{Z}_2)^m, \]

其中 \(n = \# N, m = \# E\)。

Proof：线性空间和其对偶空间的维数相同。由 Lemma 2.124 可得第一个同构关系。

容易验证 \(f: C_0\rightarrow C^0\)

\[\forall A_i\in N_G, \forall x = \sum_i A_i\in C_0, \quad f(x) = \sum_i A_i^* \]

是同构。

由 Lemma 2.123，每个 \(k\)-反链可唯一由每个顶点处的赋值组合来确定，因此可得第二个同构关系。

Lemma 2.126 反链 \(s\) 在链 \(a\) 处的取值可以定义为内积

\[s(a) = \langle s, a\rangle. \]

2.4.3 对偶同态

Definition 2.127（对偶同态） 群同态 \(h: L\rightarrow K\) 的对偶同态 \(h^*: K^*\rightarrow L^*\) 定义为

\[\forall x\in L, \forall y^*\in K^*, \quad h^*(y^*)(x) = (y^*\circ h)(x). \]

Example 2.128 对 \(L = \mathbb{Z_2\times Z_2}\) 和 \(K = \mathbb{Z_2}\)，给出所有 \(h: L\rightarrow K\) 的对偶同态 \(h^*\)。

由 Lemma 2.116，\(K^* = \{0^*, 1^*\}\)。

\[\forall (x,y)\in L, \quad h^*(z) = \begin{cases} (x,y)\mapsto 0, &z = 0^*; \\ (x,y)\mapsto h(x,y), &z = 1^*, \\ \end{cases} \]

Exercise 2.129 求 \((\mathbb{Z}_2)^n\rightarrow \mathbb{Z}_2\) 的同态的数量。

Proof：设 \(x = (x_1,\dots,x_n)\)，令 \(s^*(a) = \langle s,a\rangle = \sum_{i=1}^ns_ia_i\)，则 \(s^*\) 与 \(\mathbb{Z}_2^n\) 的元素构成一一对应。即同态数共有 \(2^n\) 个。

Exercise 2.130 对 \(L = \mathbb{Z}_2\) 和 \(K = \mathbb{Z_2\times Z_2}\)，给出所有 \(h: L\rightarrow K\) 的对偶同态 \(h^*\)。

Proof：\(L\rightarrow K\) 的同态可以由 \(h(1)\) 唯一确定。对偶同态可表示为

\[h^*(y^*) = \langle h(1),y\rangle^*. \]

2.4.4 反链映射

**Definition 2.131（\(k\)-反链映射） **图映射 \(f: G\rightarrow J\) 的 \(k\)-反链映射 \(f^k: C^k(J)\rightarrow C^k(G)\) 定义为

\[\forall a\in C_k(G), \forall t\in C^k(J), \quad f^k(t)(a) := tf_k(a). \]

Corollary 2.132 \(k\)-反链映射是 \(k\)-链映射的对偶同态。

Corollary 2.133 \(k\)-反链映射是 \(k\)-链映射的对偶映射。

Example 2.134 考虑图 \(G = (N,E)\) 和图映射 \(f: G\rightarrow G\)：

\[N := \{1,2,3,4\}, E := \{12,23,34\}, f(1)=2,f(2)=3,f(3)=f(4)=4. \]

给出链映射和反链映射的形式化表达。

可以用矩阵表示 \(0\)-链映射。将每个基础 \(0\)-链 \(x\) 表示为单位列向量 \(e_x\)，群单位元表示为 \(0\)。则 \(0\)-链映射可以表示为

\[M_0 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ \end{bmatrix} \]

考虑 \(f^0: C^0\rightarrow C^0\) 在四个基础 \(0\)-反链 \(x^*, x = 1,2,3,4\) 上的作用。由 Definition 2.131,2.122 可得

\[\begin{aligned} & f^0(x^*)(y) = x^*\circ f_0(y)\\ \Rightarrow & \begin{cases} \forall y\in C_0, f^0(1^*)(y) = 0 \Rightarrow f^0(1^*) = 0; \\ f^0(2^*) = 2^*\circ f_0 = 1^*; \\ f^0(3^*) = 3^*\circ f_0 = 2^*; \\ f^0(4^*) = 4^*\circ f_0 = 3^* + 4^*. \end{cases} \end{aligned} \]

因此 \(0\)-反链映射的矩阵

\[M^0 = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \]

注意到 \((M_0)^T = M^0\)。类似地，\(1\)-链和 \(1\)-反链为

\[M_1 = \begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{bmatrix}, \quad M^1 = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix} \]

Exercise 2.135 推导下面的链和反链的矩阵。

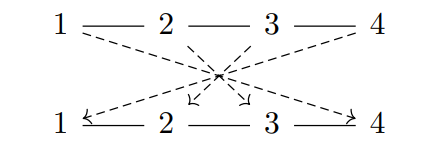
Proof：

\[\begin{aligned} M_0 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix}, \quad &M^0 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix},\\ M_1 = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{bmatrix}, \quad &M^1 = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{bmatrix}. \end{aligned} \]

2.4.5 反边界算子

Definition 2.136（反边界算子）图 \(G\) 的反边界算子 \(\mathrm{d}: C^0(G)\rightarrow C^1(G)\) 定义为

\[\forall a\in C_1(G), \forall Q\in C^0(G), \quad \mathrm{d}(Q)(a) := Q\partial(a). \]

Corollary 2.137 反边界算子是边界算子的对偶同态。

Corollary 2.138 反边界算子是边界算子 \(\partial: C_1\rightarrow C_0\) 的对偶映射。

Example 2.139 考虑图 \(G = (N_G,E_G)\)，

\[\begin{aligned} N_G &= \{A,B,C,D,E,F\}, \\ E_G &= \{AB,BC,AD,AE,BE,DF\}. \end{aligned} \]

导出 \(\mathrm{d}A^*\)。

对任意 \(AY\in E_G\)，由 Definition 2.136，

\[\mathrm{d}(A^*)(AY) = A^*\partial(AY) = A^*(A+Y) = 1. \]

类似地，\(\mathrm{d}A^*\) 在任意不与 \(A\) 相邻的边上的取值都为 \(0\)。因此有

\[\mathrm{d}A^* = \sum_{e_A\in E_G} e_A^* = AB^* + AC^* + AD^* + AE^*. \]

Lemma 2.140 基本 \(0\)-反链 \(A^*\) 的反边界算子是全体与 \(A\) 相邻的边对应的基本 \(1\)-反链的和。即

\[\forall A\in N, \mathrm{d}A^* = \sum_{AY\in E} (AY)^*. \]

Exercise 2.141 导出下图的反边界算子对应的矩阵 \(M_\mathrm{d}\)，并验证 \(M_{\mathrm{d}} = M_\partial^T\)。

Solution：

\[M_\partial = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}, \quad M_\mathrm{d} = \begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ \end{bmatrix},\\ \]

故 \(M_\mathrm{d} = M_\partial^T\)。