平衡树模板小记

\[平衡树(Balanced~Binary~Tree)~模板小记 \]

基础概念：二叉搜索树\((Binary~Search~Tree)\)

二叉树
\(leftchild<root<rightchild\)
左子树与右子树均为\(BST\)

平衡树常用种类：\(Splay,Treap,AVL~Tree\) 红黑树等
普通的\(BST\)操作\((\)如\(add,query,delete)\) 复杂度一般为\(O(log_n)\) 但如果这棵树非常不平衡如树链复杂度就会退化成\(O(n)\)

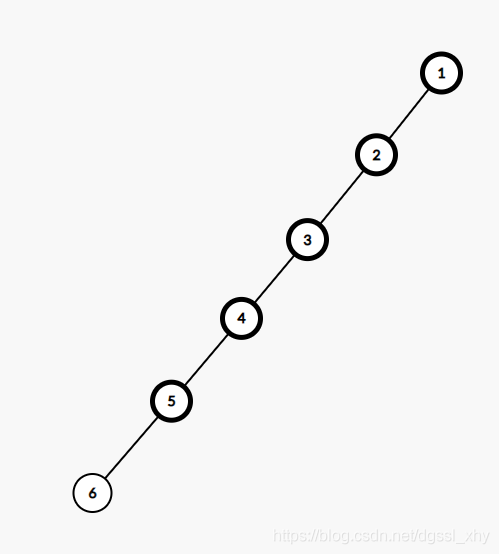
这时就需要平衡树来维持树的平衡使复杂度稳定在\(O(log_n)\)

基础操作：

插入\(x\)
删除\(x\)
查询\(x\)的排名
查询排名为\(x\)的数
求\(x\)的前驱\(/\)后继

因为\(BST\)的性质只需将排名为 \(l-1~(\)区间的前\(1\)个数\()\) 的点 \(splay\) 到 \(root\) 然后将排名为 \(r+1~(\)区间后\(1\)个数\()\) 的点 \(splay\) 到 \(root\) 的 \(rightchild\)
下传标记时交换左右子树并将翻转标记全部\(xor~1\) 最后整棵树的中序遍历就是全部翻转完的序列
这样即可实现区间翻转非常\(nb\)

\(Treap：\)

字面可得：\(treap=tree+heap\)
\(treap\)与普通\(BST\)不同它还记录一个优先级
对于优先级的选定可以直接随机\((rand)\) 随机顺序建立的\(BST\)期望高度为\(log_n\)

最重要的旋转\((rotate)\)操作：

点击查看代码

inline void Rotate(int &x,int d)
{
	int tmp=tree[x][d^1];
	tree[x][d^1]=tree[tmp][d];
	tree[tmp][d]=x;
	x=tmp;
	up(tree[x][d]);
	up(x);
}

\(d\)为旋转的方向 \(0\)为左旋 \(1\)为右旋旋转后仍然满足\(BST\)的性质

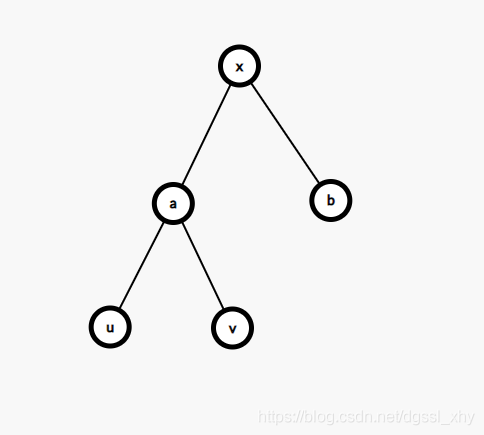
右旋后变为 \((\)左旋回去同理\()：\)

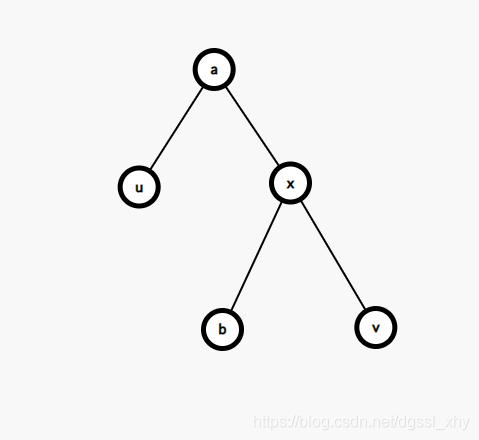
基于\(rotate\)操作就有了插入\((insert)\) 删除\((remove)\) 查询排名\((rank)\) 等操作注意会有两个哨兵节点
复杂度均为\(O(log_n)\)

基本步骤即注意保证\(BST\)的优先级然后与左儿子交换右旋与右儿子交换左旋

模板：\([普通平衡树]\)

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib> 
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,root,tot;
int tree[N][2],val[N],dat[N],size[N],cnt[N];
inline int add(int x)
{
	val[++tot]=x;
	dat[tot]=rand();
	size[tot]=cnt[tot]=1;
	return tot;
}
inline void up(int x){size[x]=size[tree[x][0]]+size[tree[x][1]]+cnt[x];}
inline void build()
{
	root=add(-inf);
	tree[root][1]=add(inf);
	up(root);
}
inline void Rotate(int &x,int d)
{
	int tmp=tree[x][d^1];
	tree[x][d^1]=tree[tmp][d];
	tree[tmp][d]=x;
	x=tmp;
	up(tree[x][d]);
	up(x);
}
inline void insert(int &x,int k)
{
	if(!x)
	{
		x=add(k);
		return;
	}
	if(k==val[x]) cnt[x]++;
	else
	{
		int d=(k<val[x])?0:1;
		insert(tree[x][d],k);
		if(dat[x]<dat[tree[x][d]]) Rotate(x,d^1);
	}
	up(x);
}
inline void Remove(int &x,int k)
{
	if(!x) return;
	if(k==val[x])
	{
		if(cnt[x]>1)
		{
			cnt[x]--;
			up(x);
			return;
		}
		if(tree[x][0]||tree[x][1])
		{
			if(!tree[x][1]||dat[tree[x][0]]>dat[tree[x][1]])
				Rotate(x,1),Remove(tree[x][1],k);
			else 
				Rotate(x,0),Remove(tree[x][0],k);
			up(x);
		}
		else x=0;
		return;
	}
	if(k<val[x]) Remove(tree[x][0],k);
	else Remove(tree[x][1],k);
	up(x);
}
inline int Rank(int x,int k)
{
	if(!x) return -2;
	if(k==val[x]) return size[tree[x][0]]+1;
	else if(k<val[x]) return Rank(tree[x][0],k);
	else return size[tree[x][0]]+cnt[x]+Rank(tree[x][1],k);
}
inline int query(int x,int rank)
{
	if(!x) return inf;
	if(rank<=size[tree[x][0]]) return query(tree[x][0],rank);
	else if(rank<=size[tree[x][0]]+cnt[x]) return val[x];
	else return query(tree[x][1],rank-size[tree[x][0]]-cnt[x]);
}
inline int Pre(int k)
{
	int x=root,pre=0;
	while(x)
	{
		if(val[x]<k) pre=val[x],x=tree[x][1];
		else x=tree[x][0];
	}
	return pre;
}
inline int Suf(int k)
{
	int x=root,suf=0;
	while(x)
	{
		if(val[x]>k) suf=val[x],x=tree[x][0];
		else x=tree[x][1];
	}
	return suf;
}
int main(){
	scanf("%d",&n);
	build();
	for(int i=1,op,x;i<=n;i++)
	{
		scanf("%d%d",&op,&x);
		if(op==1) insert(root,x);
		else if(op==2) Remove(root,x);
		else if(op==3) printf("%d\n",Rank(root,x)-1);
		else if(op==4) printf("%d\n",query(root,x+1)); 
		else if(op==5) printf("%d\n",Pre(x));
		else if(op==6) printf("%d\n",Suf(x));
	}	
	return 0;
}

\(Splay：\)

可以用来维护序列如翻转 \((\)上文提及\()\) 这样\(splay\)就是棵区间树而非权值树要维护父指针
\(splay\)更像是有目的的旋转将\(x\)旋转直到变成\(rank\)的儿子一般旋转一次复杂度没有什么优化要旋转两次
并且\(splay\)要考虑自己父亲祖父三点共线的情况看是先旋转自己还是父亲最后肯定要旋转一次自己

点击查看代码

inline void splay(int &x,int rank)
{
	while(rank^x)
	{
		int qwq=fa[rank],qaq=fa[qwq];
		if(qwq^x)
		{
			if((tree[qwq][0]==rank)^(tree[qaq][0]==qwq))  //三点共线
				rotate(x,rank);
			else rotate(x,qwq);
		}
		rotate(x,rank);
	}
}

翻转序列模板：\([文艺平衡树]\)

\(Splay~Code：\)

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,T,root,tot,ans[N];
int fa[N],tree[N][2],size[N],tag[N];
inline void up(int x){size[x]=size[tree[x][0]]+size[tree[x][1]]+1;}
inline void down(int x)
{
	if(tag[x])
	{
		swap(tree[x][0],tree[x][1]);
		tag[tree[x][0]]^=1;
		tag[tree[x][1]]^=1;
		tag[x]=0;
	}
}
inline void rotate(int &x,int rank)
{
	int qwq=fa[rank],qaq=fa[qwq],d;
	if(tree[qwq][0]==rank) d=1;
	else d=0;
	if(qwq==x) x=rank;
	else
	{
		if(tree[qaq][0]==qwq) tree[qaq][0]=rank;
		else tree[qaq][1]=rank;
	}
	tree[qwq][d^1]=tree[rank][d];
	fa[tree[qwq][d^1]]=qwq;
	tree[rank][d]=qwq;
	fa[qwq]=rank;
	fa[rank]=qaq;
	up(qwq);up(rank);
}
inline void splay(int &x,int rank)
{
	while(rank^x)
	{
		int qwq=fa[rank],qaq=fa[qwq];
		if(qwq^x)
		{
			if((tree[qwq][0]==rank)^(tree[qaq][0]==qwq))
				rotate(x,rank);
			else rotate(x,qwq);
		}
		rotate(x,rank);
	}
}
inline void build(int l,int r,int p)
{
	if(l>r) return;
	int mid=(l+r)>>1;
	if(mid<p) tree[p][0]=mid;
	else tree[p][1]=mid;
	fa[mid]=p;
	size[mid]=1;
	if(l==r) return;
	build(l,mid-1,mid);
	build(mid+1,r,mid);
	up(mid);
}
inline int Rank(int x,int rank)
{
	down(rank);
	if(x==size[tree[rank][0]]+1) 
		return rank;
	if(x<=size[tree[rank][0]])
		return Rank(x,tree[rank][0]);
	else return Rank(x-size[tree[rank][0]]-1,tree[rank][1]);
}
inline void Reverse(int l,int r)
{
	int x=Rank(l,root),y=Rank(r,root);
	splay(root,x);
	splay(tree[x][1],y);
	tag[tree[y][0]]^=1;
}
int main(){	
	scanf("%d%d",&n,&T);
	root=(n+3)>>1;
	build(1,n+2,root);
	while(T--)
	{
		int l,r;
		scanf("%d%d",&l,&r);
		Reverse(l,r+2);
	}
	for(int i=2;i<=n+1;i++)
		ans[++tot]=Rank(i,root)-1;
	for(int i=1;i<=tot;i++)
		printf("%d ",ans[i]);
	return 0;
}

posted @ 2022-01-19 10:26 EschatonRin 阅读(26) 评论(0) 收藏举报

刷新页面返回顶部

Rin

平衡树 模板小记

\(Treap：\)

\(Splay：\)

\(Splay~Code：\)

公告

平衡树模板小记