初等数论------矩阵快速幂

1月份的时候讲过矩阵快速幂但是早就忘得差不多了捡一下（）

昨天讲的矩快板子愣是卡了我半天最后才发现取模取早了｛捂脸｝

昨天（2022.7.27）朱德远过生日诶

生快生快🎂！！！

来直入主题：

一矩阵相关：

1、定义

矩阵顾名思义一个矩形的方阵

在百科中写到：

矩阵是一个按照长方阵列排列的复数或实数集合

总之，矩阵就是一堆数，按照矩形排列形成的集合

那么，我们所需要记录的也就是它的长、宽以及矩阵中存储的元素

特殊的，长宽相等的矩阵我们定义它为方阵

当两个矩阵的长宽相等时，我们认为这两个矩阵为同型矩形

2、基本运算

加法运算：

在矩阵加法中两个矩阵可相加的前提是 两个矩阵为同型矩阵；

此时我们只需将对应位置的元素相加即可（）如下：

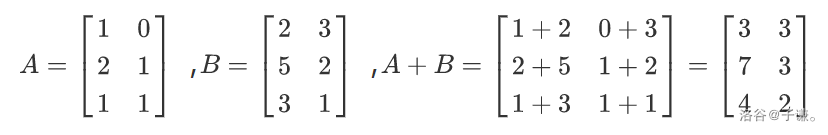
在矩阵的加法运算中，满足交换律和结合律，也就是

减法运算：

相类比于加法运算两个矩阵可相减的前提也是 两个矩阵为同型矩阵；

由于减法是加法的逆运算所以对应的我们只需要将两个矩阵对应的元素相减即可（）如下：

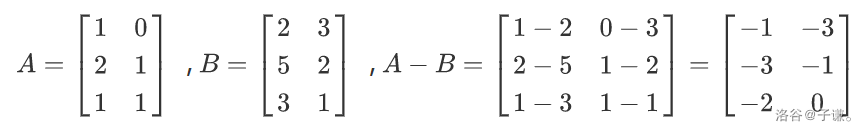
数乘运算：

由于实数中不存在数乘的概念所以我们用向量的只是来理解这个数乘

我们钦定矩阵的型不变因此我们只将系数与元素相乘如下（）：

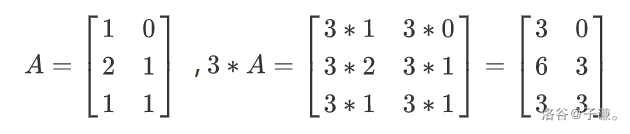
在数乘中满足下列定律：

$(λ μ) A$

即：

满足A矩阵的列数等于B矩阵的行数

设A矩阵为m * k,B矩阵为k * n，则A、B可以相乘相乘后得到的矩阵C大小为 m * n；

那么怎么相乘呢（？）

非常简单

用A的第i行元素与B的第j列对应元素依次相乘并相加就得到了C矩阵中的第i，j位的元素

这么说是不是很懵（？）

我们来看个图就清晰了：

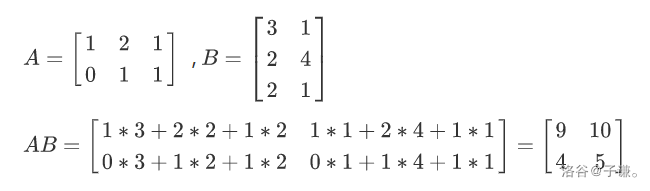
就是像这样（）；

在矩阵乘法中满足以下运算律：

然而在乘法中我们都知道 1乘以任何数都等于这个数

在矩阵乘法中矩阵也有自己的1 但它并不是数字1 而是：

单位矩阵

单位矩阵的特点：在一个大小为m * n的矩阵中单位矩阵的大小为n * n，我们称之为n阶方阵即一个正方形矩阵；

它的内部元素中从左上至右下均为1 剩下元素均为0；

二、矩阵快速幂

OK矩阵的基本运算就这样讲完了（完结撒花）

接下来进入正题：矩阵快速幂

矩阵快速幂其实就是在快速幂中将矩阵相乘即可

1月份的时候我写的是函数 lyn学长给我们讲了重载运算符看上去更加清晰简便那我们就来讲一下重载运算符：

首先先开一个结构体用来存储矩阵

在结构体中我们需要两个函数一个用来将矩阵清零一个用来预处理构造单位矩阵：

 1 struct M{
 2     int a[101][101];
 3     inline void clean(){
 4         for(register int i(1);i <= n;i ++){
 5             for(register int j(1);j <= n;j ++){
 6                 a[i][j] = 0;
 7             }
 8         }
 9     }//也可以写成 memset（a,0,sizeof(a)）;
10     inline void init(){
11         for(register int i(1);i <= n;i ++){
12             a[i][i] = 1;
13         }
14     }
15 }A;

接下来我们需要重载乘号运算符：

 1 inline M operator *(const M&x,const M&y){
 2     M z;
 3     z.clean();//相乘之前必须先将存储矩阵清零
 4     for(register int i(1);i <= n;i ++){
 5         for(register int j(1);j <= n;j ++){
 6             for(register int k(1);k <= n;k ++){
 7                 z.a[i][j] += (x.a[i][k] * y.a[k][j]) % mod;
 8                 z.a[i][j] %= mod;//记得取模！！！！！！（我就卡在这了）    
 9             }
10         }
11     }
12     return z;
13 }

接下来就是传统的快速幂算法：

 1 inline M qpow(M a,int b){
 2     M res;
 3     res.init();//先预处理构造单位矩阵
 4     while(b){
 5         if(b & 1){
 6             res = res * a;
 7         }
 8         a = a * a;
 9         b >>= 1;
10     }
11     return res;
12 }

就这样矩阵快速幂的函数部分就完成了！！！！！

带来AC大代码（题目链接）：

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <climits>
 6 #include <cmath>
 7 #include <cassert>
 8 #include <set>
 9 #include <map>
10 #include <stack>
11 #include <queue>
12 #define int long long
13 using namespace std;
14 inline int read(){
15     int x = 0,f = 1;
16     char ch = getchar();
17     while(ch < '0' || ch > '9'){
18         if (ch == '-') f = -1;
19         ch = getchar();
20     }
21     while(ch >= '0' && ch <= '9'){
22         x = x * 10 + ch - '0';
23         ch = getchar();
24     }
25     return x * f;
26 }
27 const int mod = 1e9 + 7;
28 int n;
29 int k;
30 struct M{
31     int a[101][101];
32     inline void clean(){
33         for(register int i(1);i <= n;i ++){
34             for(register int j(1);j <= n;j ++){
35                 a[i][j] = 0;
36             }
37         }
38     }
39     inline void init(){
40         for(register int i(1);i <= n;i ++){
41             a[i][i] = 1;
42         }
43     }
44 }A;
45 inline M operator *(const M&x,const M&y){
46     M z;
47     z.clean();
48     for(register int i(1);i <= n;i ++){
49         for(register int j(1);j <= n;j ++){
50             for(register int k(1);k <= n;k ++){
51                 z.a[i][j] += (x.a[i][k] * y.a[k][j]) % mod;
52                 z.a[i][j] %= mod;    
53             }
54         }
55     }
56     return z;
57 }
58 inline M qpow(M a,int b){
59     M res;
60     res.init();
61     while(b){
62         if(b & 1){
63             res = res * a;
64         }
65         a = a * a;
66         b >>= 1;
67     }
68     return res;
69 }
70 signed main(){
71     M p;
72     M q; 
73     p.init();
74     n = read();
75     k = read();
76     for(register int i(1);i <= n;i ++){
77         for(register int j(1);j <= n;j ++){
78             A.a[i][j] = read();
79         }
80     }
81     p = qpow(A,k);
82     for(register int i(1);i <= n;i ++){
83         for(register int j(1);j <= n;j ++){
84             cout << p.a[i][j] << " ";
85         }
86         cout << endl;
87     } 
88     return 0;
89 }

带来一道板子题（题目链接）

题目描述

大家都知道，斐波那契数列是满足如下性质的一个数列：

$F_{n} =$

${$

$1 (n \leq 2)$

$F_{n - 1} + F_{n - 2} (n \geq 3)$

请你求出 $109+7F_n \bmod 10^9 + 7$ 的值。

输入格式

一行一个正整数

输出格式

输出一行一个整数表示答案。

输入输出样例

输入 #1

输出 #1

输入 #2

输出 #2

说明/提示

【数据范围】
对于 $60%60\%$ 的数据，；
对于 $100%100\%$ 的数据， $1≤n<2631\le n < 2^{63}$ 。

这个问题就非常简单不过对于初学矩阵的同学构造这个矩阵还是有点难度的：

首先由于这个该死的数据范围我们无法使用普通的递推去完成这个问题

于是我们可以使用转移矩阵来加速：

我们知道在斐波那契数列中 f[i] = f[i - 1] + f[i - 2];

那也就是说

我们可以用这个关系去推导转移矩阵、

设f相关矩阵为

|f[i] |

|f[i - 1 |

我们想用一个转移矩阵去建立f[i] f[i - 1] 和 f[i - 1] f[i - 2] 之间的关系

于是我们设出一个转移矩阵

|a b|

|c d|

当我们把转移矩阵和递推阵相乘的时候

我们就会得到

|a b| \ / |f[i - 1]| ----- |af[i - 1] + bf[i]| ----- |f[i] |

|c d| / \ |f[i - 2]| ----- |cf[i - 1] + df[i]| ----- |f[i - 1]|

(实在没有办法了只能用这种符号表示一下乘法大家感性理解吧（））

此时我们就可以得到为了使左右等式成立我们可以

令c = 1,d = 0得到f[i - 1]

令a = 1,b = 1得到f[i](根据斐波那契公式f[i] = f[i - 1] + f[i - 2]）

这样一来我们就得到了以矩阵为单位的转移式

由此而推我们可以一直把i - 1 i - 2推广到1 和 2 那也就是说最后一个转移点在f[1] 和 f[2]上

那么式子就变成了

|1 1| ⁿ\ / |f[1]| ----- |f[i] |

|1 0| / \ |f[2]| ----- |f[i - 1]|

那么这个n应该等于多少呢

从最大的i 也就是n开始到2 总共经历了n - 2次递推

所以转移矩阵自我相乘了n - 2次

也就是n - 2次方

由此该问题就此解决

我们用矩阵快速幂就可以解决这个问题

来来来上代码：

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <climits>
 6 #include <cmath>
 7 #include <cassert>
 8 #include <set>
 9 #include <map>
10 #include <stack>
11 #include <queue>
12 #define int long long
13 using namespace std;
14 inline int read(){
15     int x = 0,f = 1;
16     char ch = getchar();
17     while(ch < '0' || ch > '9'){
18         if (ch == '-') f = -1;
19         ch = getchar();
20     }
21     while(ch >= '0' && ch <= '9'){
22         x = x * 10 + ch - '0';
23         ch = getchar();
24     }
25     return x * f;
26 }
27 const int mod = 1e9 + 7;
28 int n;
29 struct M{
30     int a[101][101];
31     inline void clean(){
32     memset(a,0,sizeof(a));
33     }
34     inline void init(){
35         for(register int i(1);i <= 101;i ++){
36             a[i][i] = 1;
37         }
38     }
39 }A;
40 inline M operator *(const M&x,const M&y){
41     M z;
42     z.clean();
43     for(register int i(1);i <= 10;i ++){
44         for(register int j(1);j <= 10;j ++){
45             for(register int k(1);k <= 10;k ++){
46                 z.a[i][j] += (x.a[i][k] * y.a[k][j]) % mod;
47                 z.a[i][j] %= mod;    
48             }
49         }
50     }
51     return z;
52 }
53 inline M qpow(M a,int b){
54     M res;
55     res.init();
56     while(b){
57         if(b & 1){
58             res = res * a;
59         }
60         a = a * a;
61         b >>= 1;
62     }
63     return res;
64 }
65 signed main(){
66     M p;
67     M q; 
68     p.init();
69     scanf("%lld",&n);
70     if(n <= 2) return cout << 1 << endl,0; 
71     A.a[1][1] = 1;
72     A.a[1][2] = 1;
73     A.a[2][1] = 1;
74     A.a[2][2] = 0;//构造转移矩阵
75     p = qpow(A,n - 2);
76     M g;
77     g.a[1][1] = 1;
78     g.a[2][1] = 1;//斐波那契初始f[1]f[2]
79     q = p * g;
80     printf("%lld\n",q.a[1][1] % mod); 
81     return 0;
82 }

完结撒花！！

数论难死。。。。。。。。。。

posted @ 2022-07-28 11:20 November&&Rain 阅读(143) 评论(0) 收藏举报

刷新页面返回顶部

初等数论------矩阵快速幂

一 矩阵相关：