初等数论 ------ 素数与素数筛

集训开始啦！！！！！！！！！（2022.7.25)

(今儿沉淀物过生日啊 生快🎂）

先进入正题 ： 初等数论

今天讲了太多东西了我去「捂脸」 理不过来了

刘曜宁学长太强了 但是他讲的真的好快「捂脸」

新高一的孩子们也来了 新的征程这就开始了呗

先来第一个知识点：素数和素数筛

一 素数定理：

    令 π(n) 为小于等于 n 的素数个数，有 π(n)=Θ(n/lnn)

 

 

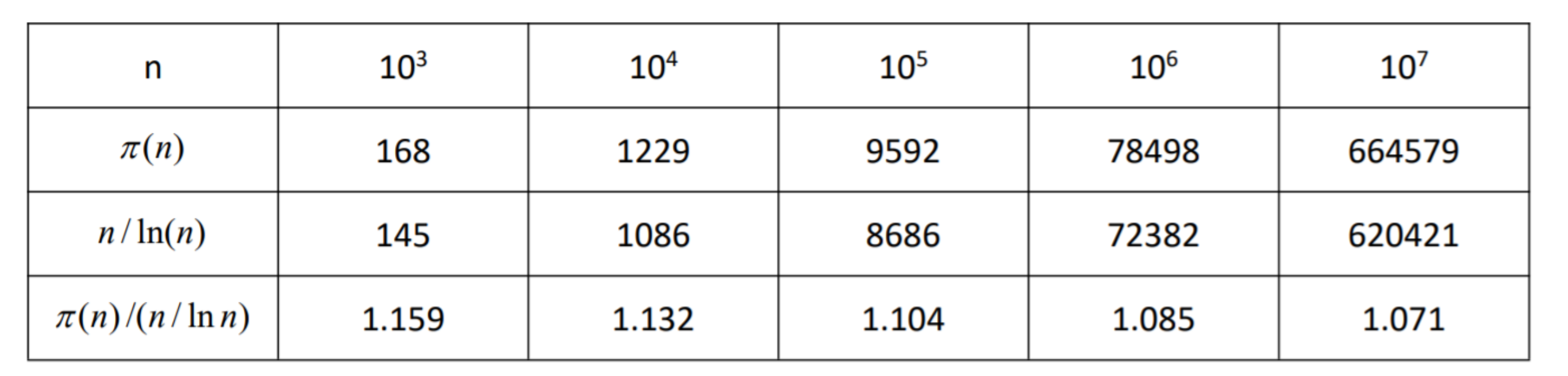
据说这个东西没啥用 但是算复杂度的时候比较有用（）

二 素数判定和素数筛：

1、单点筛O(√n)

 

 

比较慢（）

2、埃氏筛O(nloglogn)

 

 

 

非常经典 但是也很慢（）

3、线性筛（欧拉筛）O(n)

inline void oula(){
    for(register int i(2);i <= n;i ++){
        if(!vis[i]) p[++ cnt] = i;
        for(register int j(1);i * p[j] <= n;j ++){
            vis[i * p[j]] = 1;
            if(i % p[j] == 0) break;
        }
    }
}

非常强（）

 

欧拉筛法简便的原理：

埃氏筛的缺点在于它会把在范围内的每一个因数都标记一遍 就会出现很多重复标记 大大增加复杂度；

使用欧拉筛时 例如当i = 4，j = 1时，i * p[j] = 8,i % p[j] = 0；

此时则退出循环；

因为i % prime[j] = 0，故i = t * prime[j]，所以i * prime[j + 1] = t * prime[j] * prime[j + 1],相当于是prime[j]的倍数(已经被标记过)，所以这样就会造成重复标记，因此我们退出循环。

怎么样是不是很强（）