二分图 + 二分图最大匹配
首先
hhs tql!!!!!!!!!
无意冒犯于lzb和hbc 但hhs这个是三个同学中我唯一一个听懂了的();
二分图
定义:
二分图又称作二部图,是图论中的一种特殊模型。
设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y,并且图中每条边连接的两个顶点一个在X中,另一个在Y中,则称图G为二分图。
上图:
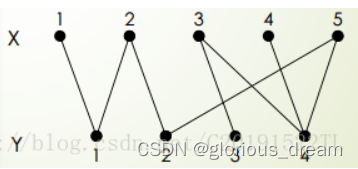
也就是说 X和Y互不干扰 独立成集 但XY之间有互通关系
性质:
当且仅当无向图G的每一个环的结数均为偶数时,G才是二分图。如果无环,相当于每个环的结点数为0,故也视为二分图。
判断是否是二分图:
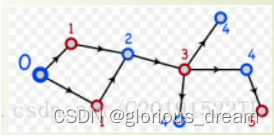
这里我们用到染色法,用两种颜色来染这个图。如果该节点的颜色是0,那么所有与其相邻的节点的颜色都是1。最后判断是否满足上述条件即可。
然而在hhs巨佬给出的代码中 他用了 1 和 2 来进行染色 因此就有了 3 - a 这一步;
1 #include <iostream> 2 #include <algorithm> 3 #include <cstdio> 4 #include <cstring> 5 #include <climits> 6 #include <cmath> 7 //#define int long long 8 #define open(x); freopen("x.in","r",stdin);freopen("x.out","w",stdout); 9 using namespace std; 10 inline int read(){ 11 int x = 0,f = 1; 12 char ch = getchar(); 13 while (ch < '0' || ch > '9'){ 14 if (ch == '-') f = -1; 15 ch = getchar(); 16 } 17 while (ch >= '0' && ch <= '9'){ 18 x = x * 10 + ch - '0'; 19 ch = getchar(); 20 } 21 return x * f; 22 } 23 const int N = 1e5 + 10; 24 int n; 25 int m; 26 int head[N]; 27 struct Edge{ 28 int to; 29 int next; 30 }e[N]; 31 int color[N]; 32 int cnt = -1; 33 inline void add_edge(int u,int v){ 34 e[++ cnt].to = v; 35 e[cnt].next = head[u]; 36 head[u] = cnt; 37 } 38 inline bool dfs(int x,int c) {//判断 x 点是否可染 c 颜色 39 color[x] = c; //给 x 染 c 色, c = 1 or 2 40 for(register unsigned i = head[x];i;i = e[i].next){ 41 int j = e[i].to; 42 if(!color[j]) //如果j点未被染色,判断它染另一种颜色是否合理。 43 if(!dfs(j,3-c)) return 0; //c = 1时,另一种颜色为 3 - 1 = 2 44 else if(color[j] == c) return 0; //如果 j 点与 x 点颜色相同, 则返回false 45 } 46 return 1; 47 } 48 signed main(){ 49 n = read(); 50 m = read(); 51 memset(head,-1,sizeof(head)); 52 for(register unsigned i(1);i <= m;i ++){ 53 register int u = read(); 54 register int v = read(); 55 add_edge(u,v); 56 add_edge(v,u); 57 } 58 bool flag = 1; 59 for(register unsigned i(1);i <= n;i ++){//从1点开始,将未被染色的点染上1颜色。 60 if(!color[i]){ 61 if(!dfs(i,1)){ 62 flag = 0; 63 break; 64 } 65 } 66 } 67 if(flag) cout << "Yes" << endl; 68 else cout << "NO" << endl; 69 return 0; 70 } 71
二分图最大匹配:
首先什么是匹配:
给定一个二分图G,在G的一个子图M中, M的边集{E}中的任意两条
边都不交汇于同一个结点,则称M是一个匹配。
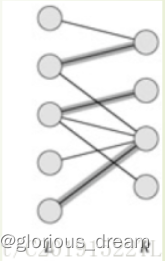
举个例子(来自hhs巨佬的生动讲解):
我们把左点集看作是要买房子的人,右点集是正在出售的房子;
第一个人发现 当他来到第一栋房子的时候 第一栋房子还没有人来过且没有人买 那么第一栋房子就可以被标记为有人来过;
第二个人来到这里 发现这个房子有人来过了 于是就前往下一栋 也就是第三栋房子
当他发现这里没人来过的时候 他就是这栋房子的主人了
以此类推 我们要尽可能的让更多的人买到与之对应的唯一的房子
这就是最大匹配
那么如何求出最大匹配?
这里有一个很经典的算法:
匈牙利算法
算法流程:
1.
从任意一个没有被配对的点x开始,从点x的边中任意选一条边。
如果此时点i没有被配对那么配对成功,则找到了一条增广路。
如果点i此时已经被配对了,那么可以尝试将点i与其他点配对
。如果尝试成功,则找到一条增广路。
这里用match[ ]来记录配对关系, 即match[i] = x。
并且将配对数 + 1。 这个过程我们用dfs来实现。
2.
如果配对失败,就从点x的边中重选一条边尝试。直到点x配对成功或尝试完x所有的边。
3.
接下来对没有配对的点一一进行配对,直到所有的点都尝试完毕并找不到新的增广路。
上代码
1 #include <iostream> 2 #include <algorithm> 3 #include <cstdio> 4 #include <cstring> 5 #include <climits> 6 #include <cmath> 7 #define int long long 8 #define open(x); freopen("x.in","r",stdin);freopen("x.out","w",stdout); 9 using namespace std; 10 inline int read(){ 11 int x = 0,f = 1; 12 char ch = getchar(); 13 while (ch < '0' || ch > '9'){ 14 if (ch == '-') f = -1; 15 ch = getchar(); 16 } 17 while (ch >= '0' && ch <= '9'){ 18 x = x * 10 + ch - '0'; 19 ch = getchar(); 20 } 21 return x * f; 22 } 23 const int M = 5e4 + 5; 24 int n;//n表示左侧有n个点 25 int m;//m表示右侧有m个点 26 int E;//E表示共有E条边 27 int ans = 0; 28 struct Edge{ 29 int next; 30 int to; 31 }e[M]; 32 int head[M]; 33 int cnt = 0; 34 int vis[M]; 35 int match[M]; 36 inline void add_edge(int u,int v){ 37 e[++ cnt].to = v; 38 e[cnt].next = head[u]; 39 head[u] = cnt; 40 } 41 inline bool find(int x){ 42 for(register unsigned i(head[x]);i;i = e[i].next){//遍历 43 } 44 int v = e[i].to; 45 if(!vis[v]){//当这栋房子没有人来过 46 vis[v] = 1;//我来过了!! 47 if(!match[v] || find(match[v])){//当这栋房子也没有人买 48 match[v] = x;//那他就是我的了!! 49 return 1;//这样我就买到房子了 一条路成功匹配 50 } 51 } 52 } 53 return 0;//我没买到房子呜呜呜 匹配失败 54 } 55 signed main(){ 56 n = read(); 57 m = read(); 58 E = read(); 59 for (register unsigned i(1);i <= E;i ++){ 60 register int u = read(); 61 register int v = read(); 62 add_edge(u,v); 63 } 64 for(register unsigned i(1);i <= n;i ++){ 65 memset(vis,false,sizeof(vis)); 66 if(find(i)) ans ++; 67 } 68 cout << ans << endl; 69 return 0; 70 }
完结撒花(bushi
还有一个二分图带权最大匹配 暂时没搞出来 下次更
再来一遍
hhs tql!!!!!!
本博客大量借鉴于hhs博客 https://blog.csdn.net/glorious_dream/article/details/125034451?spm=1001.2014.3001.5501
24OI Fighting!!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号