[洛谷P5361][SDOI2019]热闹又尴尬的聚会：构造题

分析

构造方法

（截图自UOJ群）

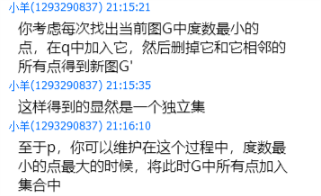
可以使用std::set维护这个过程，不过据说可以做到\(O(n+m)\)。。

正确性证明

题目中的要求等价于\((p+1)(q+1) > n\)

设每次找出地度数最小的点的被删除时的度数分别为\(d_1,d_2,...,d_q\)，显然用这些点可以构造出一个尴尬度为\(q\)的方案。

并且，我们有：

\[\sum_{i=1}^{q}(d_i+1) = n \]

考虑这个度数序列取到最大值的位置，可以发现用这个点以及在这个点之后删除的点能够构造出一个热闹度为\(\max d\)的方案。

根据上面那个式子，显然有：

\[(\max d+1) \times q \geq n \]

所以：

\[(\max d+1) \times (q+1) > n \]

正确性得证。

代码

#include <bits/stdc++.h>

#define rin(i,a,b) for(int i=(a);i<=(b);++i)
#define irin(i,a,b) for(int i=(a);i>=(b);--i)
#define trav(i,a) for(int i=head[a];i;i=e[i].nxt)
#define Size(a) (int)a.size()
#define pb push_back
#define mkpr std::make_pair
#define fi first
#define se second
#define lowbit(a) ((a)&(-(a)))
typedef long long LL;

using std::cerr;
using std::endl;

inline int read(){
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}

const int MAXN=10005;
const int MAXM=100005;

int n,m,ecnt,head[MAXN],deg[MAXN];
int len,seq[MAXN];
int cnt1,cnt2,sat[MAXN],sun[MAXN];
bool vis[MAXN];

struct Edge{
	int to,nxt;
}e[MAXM<<1];

inline void add_edge(int bg,int ed){
	++ecnt;
	e[ecnt].to=ed;
	e[ecnt].nxt=head[bg];
	head[bg]=ecnt;
}

struct node{
	int pos,deg;
	inline friend bool operator < (node x,node y){
		return x.deg==y.deg?x.pos<y.pos:x.deg<y.deg;
	}
}a[MAXN];

std::set<node> st;
typedef std::set<node>::iterator iter;

void clear(){
	ecnt=len=cnt1=cnt2=0;
	memset(head,0,sizeof head);
	memset(deg,0,sizeof deg);
	memset(vis,false,sizeof vis);
}

int main(){
	int T=read();
	while(T--){
		clear();
		n=read(),m=read();
		rin(i,1,n)a[i]=(node){i,0};
		rin(i,1,m){
			int u=read(),v=read();
			add_edge(u,v);
			add_edge(v,u);
			++deg[u];
			++deg[v];
			++a[u].deg;
			++a[v].deg;
		}
		rin(i,1,n)st.insert(a[i]);
		int maxdeg=-1,maxi=0;
		while(!st.empty()){
			int x=st.begin()->pos;
			if(deg[x]>maxdeg){
				maxdeg=deg[x];
				maxi=len;
			}
			st.erase(st.begin());
			seq[++len]=x;
			sun[++cnt2]=x;
			vis[x]=true;
			trav(i,x){
				int y=e[i].to;
				iter it=st.find((node){y,deg[y]});
				if(it==st.end())continue;
				st.erase(it);
				seq[++len]=y;
				trav(j,y){
					int ver=e[j].to;
					iter it=st.find((node){ver,deg[ver]});
					if(it==st.end())continue;
					st.erase(it);
					st.insert((node){ver,--deg[ver]});
				}
			}
		}
		rin(i,maxi+1,len)sat[++cnt1]=seq[i];
		printf("%d ",cnt1);
		rin(i,1,cnt1)printf("%d ",sat[i]);
		putchar('\n');
		printf("%d ",cnt2);
		rin(i,1,cnt2)printf("%d ",sun[i]);
		putchar('\n');
	}
	return 0;
}