<五>线性代数中的矩阵 && 矩阵运算
1.初识矩阵
1.1 从二元一次方程组开始
二元一次方程:方程中未知数的个数是两个,未知数的指数的次数是一次
二元一次方程组:两个二元一次方程就组成了一个方程组
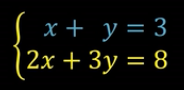
求解以上方程组有两种方法:

代入消元法是将第一个方程变形代入第二个方程。
加减消元法是将两边同时乘以一个数,然后相加消除其中的一个变量。
两种方式都是把二元一次方程变成一元一次方程然后求解。
两种方式又统称为高斯消元法。
从解析几何的角度来看,任何一个二元一次方程的本质都是一条直线。
对应方程组的解就是两条直线交点的坐标。
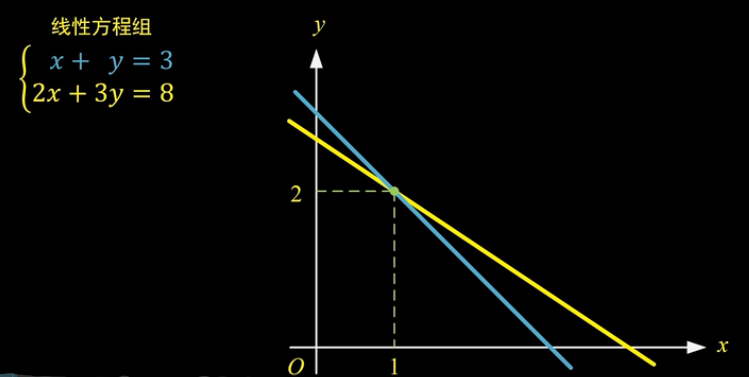
实际上,未知数指数为1的方程组还有一个更为通用的名称,叫做“线性方程组”。
对比如下为“非线性方程组”:

线性方程组可以分为两类,一种是方程组的常数项为0,叫做“齐次线性方程组”;还有一种是常数项不全为0的,叫做“非齐次线性方程组”。
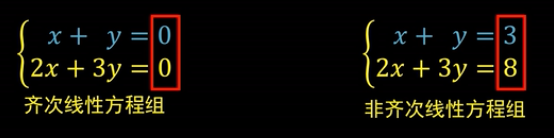
下面通过解析几何来了解线性方程组的解:
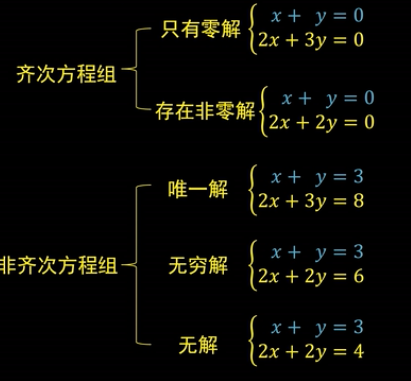
齐次线性方程组的解:
零解:
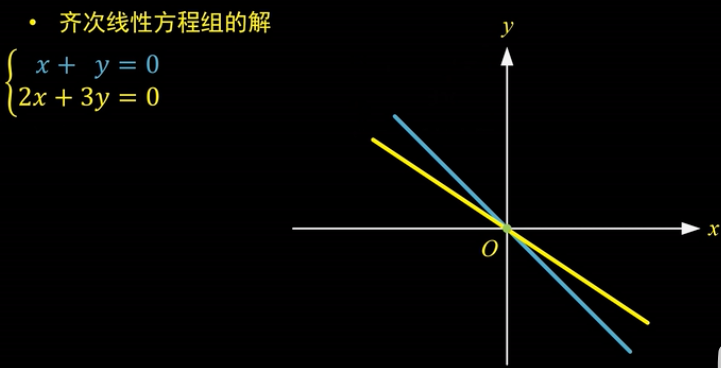
如上方程组,其中两个方程分别是过原点的两条直线,由于斜率不同,因此它们唯一的焦点就是原点。
所以说,这个齐次方程组只有“零解”。
非零解:
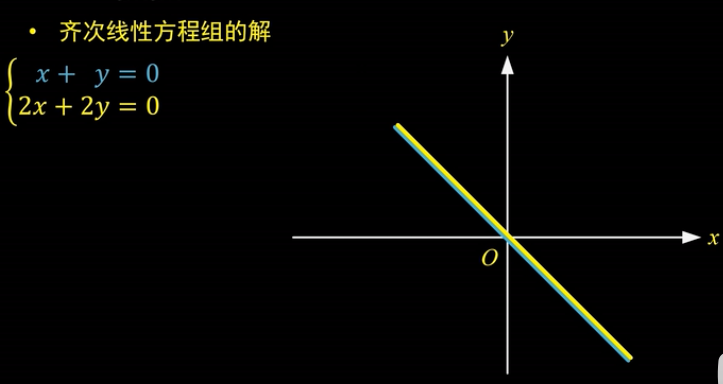
如图方程组中,第二个方程简化过后就是第一个方程,这两个方程对应的直线是重合的。也就是说,直线上的任意一个点都是方程组的解。
可以说,这个齐次线性方程组存在“非零解”,而且有无穷个非零解。
非齐次线性方程组的解:
唯一解:
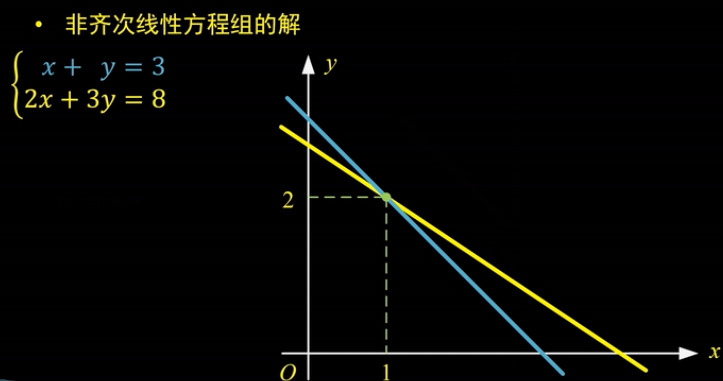
如图,两个方程组由于斜率不同,对应的直线只有一个交点。这种情况是“唯一解”。
无穷解:
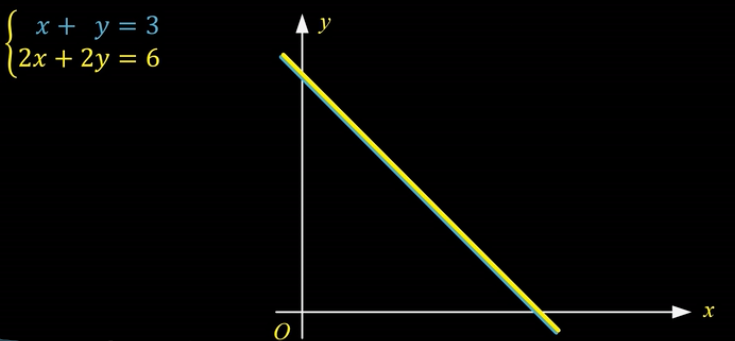
如图,两个方程组本质是一条直线(重合),直线上的任意点坐标都是方程组的解。这种情况是“无穷解”。
无解:
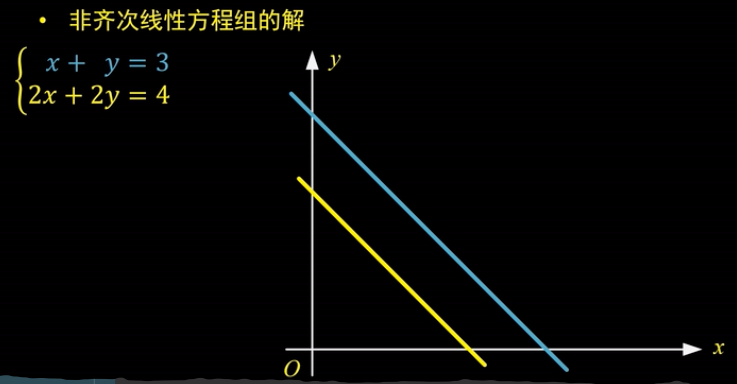
如图,两个方程对应的直线是平行的,这种情况下没有交点。也就是“无解”。
总结一下线性方程组解的情况:
二元一次线性方程组是最简单的线性方程组。
很多情况下,会遇到更复杂的线性方程组如下图示例:

一些复杂的线性方程组再通过“高斯消元法”就很难明确消元的方向性,于是就需要探索新的方法去获取方程组的解。
齐次线性方程组的一般形式:

同时,为了保证m个有效方程,n个有效未知数。

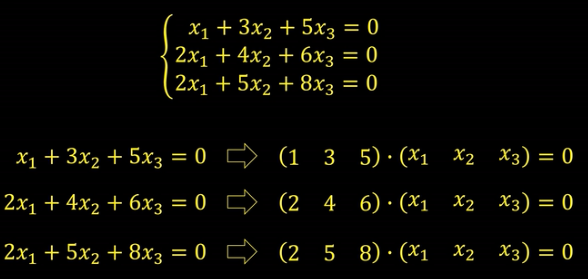

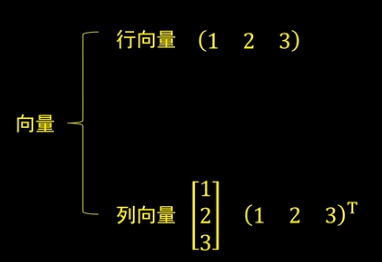



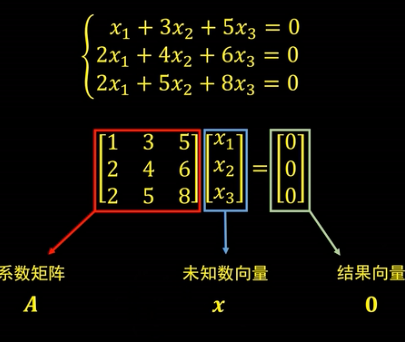

对于非齐次线性方程:
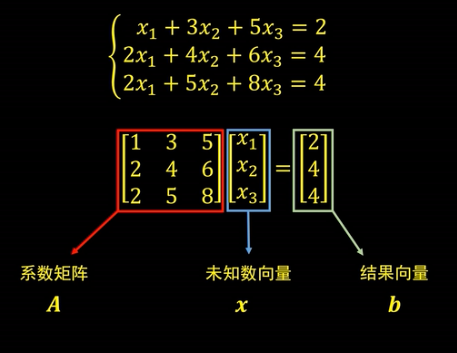






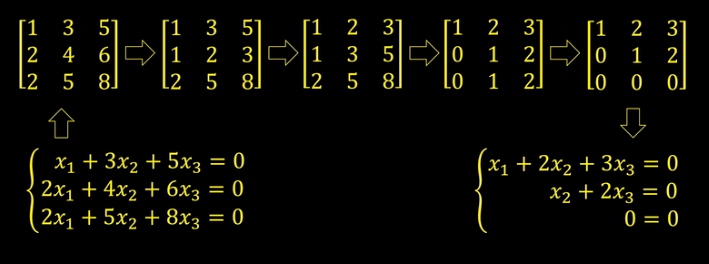



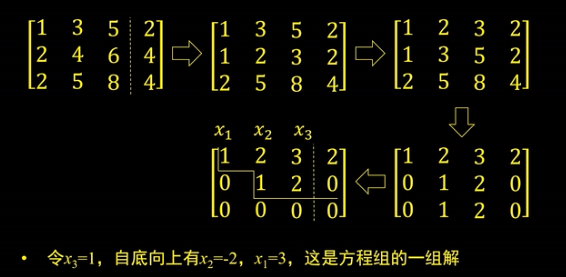

1.2 齐次线性方程组的求解
待补充。。。。。。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号