差分约束算法

【模板】差分约束算法

题目描述

给出一组包含 $m$ 个不等式，有 $n$ 个未知数的形如：

$$\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases}$$

的不等式组，求任意一组满足这个不等式组的解。

输入格式

第一行为两个正整数 $n,m$，代表未知数的数量和不等式的数量。

接下来 $m$ 行，每行包含三个整数 $c,c',y$，代表一个不等式 $x_c-x_{c'}\leq y$。

输出格式

一行，$n$ 个数，表示 $x_1 , x_2 \cdots x_n$ 的一组可行解，如果有多组解，请输出任意一组，无解请输出 NO。

样例 #1

样例输入 #1

3 3
1 2 3
2 3 -2
1 3 1

样例输出 #1

5 3 5

提示

样例解释

$\begin{cases}x_1-x_2\leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases}$

一种可行的方法是 $x_1 = 5, x_2 = 3, x_3 = 5$。

$\begin{cases}5-3 = 2\leq 3 \\ 3 - 5 = -2 \leq -2 \\ 5 - 5 = 0\leq 1 \end{cases}$

$$每个不等式称为一个约束条件，都是两个未知量之差小于或等于某个常数。$$

$$X_1 - X_2 <= Y$$

$$移项$$

$$X_1 <= X_2 + Y$$

$$我们可以把它转化为一个图论题看做X_1 \to X_2 的边权为Y的边$$

$$求最短路OR最长路即可$$

$$如果出现负环则无解$$

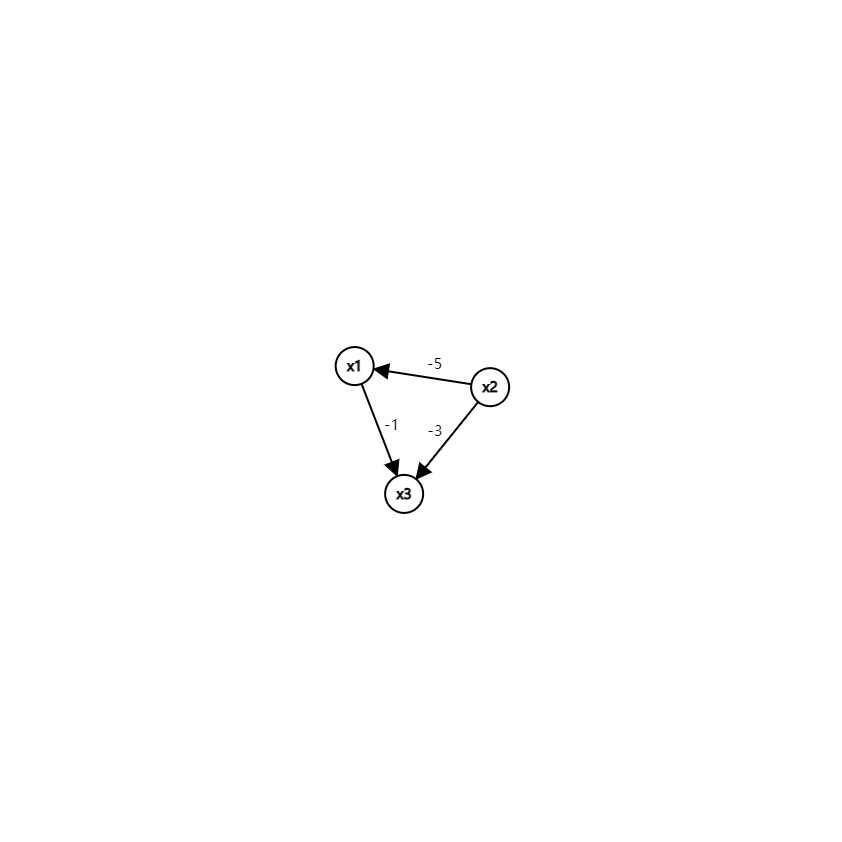
$$x1 \ne x1 -1 -3 -5$$

#include <bits/stdc++.h>

using namespace std;
const int N = 5e3 + 5;
int n,m;
struct edge
{
    int x,y,z;
};
vector<int>d;
vector<edge>e;

bool bellman_ford()
{
    for(int i = 1 ;i <= n - 1 ; i ++ )
        for(auto j : e)
        d[j.y] = min(d[j.x] + j.z,d[j.y]);
    for(auto j : e)
    if(d[j.y] > d[j.x] + j.z)
    {
        puts("NO");return 0;
    }
    for(int i = 1 ; i <= n ; i ++ )cout << d[i] << " ";
    return 0;


}

int main()
{
    cin >> n >> m;
    for(int x,y,z,i = 1 ; i <= m ;i ++ )
    {
        scanf("%d%d%d",&x,&y,&z);
        e.push_back({y,x,z});
    }
    d.resize(n +5);
    bellman_ford();
    return 0;
}

#include <bits/stdc++.h>

using namespace std;
#define vx first
#define vw second
typedef pair<int,int> pii;
const int N = 1e5 + 10;
int n,m,c;
vector<pii>g[N];
int dist[N];
bool st[N];

void spfa()
{
    memset(dist ,-0x3f ,sizeof dist);
    queue<int>q;
    q.push(0);st[0] = 1;dist[0] = 0;
    while(q.size()){
        int u = q.front();
        q.pop();st[u] = 0;
        for(auto v:g[u])
        if(dist[v.vx] < dist[u] + v.vw)
        {
            dist[v.vx] = dist[u] + v.vw;
            if(!st[v.vx])q.push(v.vx),st[v.vx] = 1;
        }
    }

}


int main()
{
    cin >> n >> m >> c;
    for(int s,i = 1 ; i <= n ; i ++ )
    {
        scanf("%d",&s);
        g[0].push_back({i,s});
    }
    for(int a,b,x,i = 1 ; i <= c ; i ++ )
    {
        scanf("%d%d%d",&a,&b,&x);
        g[a].push_back({b,x});
    }
    spfa();
    for(int i = 1 ; i <= n ; i ++ ){
        printf("%d\n",dist[i]);
    }
}