斜率优化dp学习笔记
本人太弱,如果讲的不好,请见谅。
引入
斜率优化 dp,通常用于 dp 方程长成这个样子的题:
因为有 \(a_{i}b_{j}\) 这样的与 \(i\) 和 \(j\) 都有关的恶心项,所以不能用单调队列优化(虽然斜率优化有些时候也得用单调队列)。
例题
例题 1:P3195 [HNOI2008] 玩具装箱
既然叫斜率优化 dp,那么我们肯定得先把朴素的 dp 方程写出来。设 \(dp_{i}\) 为前 \(i\) 个玩具都塞进去了的最小代价,并维护前缀和 \(sum_{i} = \sum\limits_{j = 1}^{i}C_{i} + 1\),那么有朴素的 dp 方程:
方程很好理解,这里就不说了。那么现在我们考虑优化。为了方便,把 \(L\) 提前加 \(1\),然后把式子化简一下:
化简的原则就是拆括号,然后把与内层循环无关的量扔出 \(\min\)。
考虑一次函数的斜截式 \(y = kx + b\),移项变成 \(b = y - kx\),原方程就该写作 \(b_{i} = \min\{y - kx\}\),对于每一个 \(i\),把在择优过程中不变的项(也就是只跟随 \(i\) 变化的项,因为我们在讨论一个单独的 \(i\),所以是“不变的项”)记在 \(k\) 和 \(b\) 里面,要变的(也就是会跟随 \(j\) 变化的项)记在 \(kx\) 和 \(y\) 里面,具体一点,就是最小化的(也就是被扔出 \(\min\) 的项和左边的 \(dp_{i}\),还有一种描述是只跟 \(i\) 有关的项)记作 \(b\),和 \(i,j\) 都有关的项记作 \(kx\):只与 \(i\) 有关的记作 \(k\),只与 \(j\) 有关的记作 \(x\)。剩下的只与 \(j\) 有关的项记作 \(y\)。
看上面一大段文字会迷糊,不如来看看例子。在这道题的这个方程里,有:
如果你看了还是迷糊,那么可以看看下面的例题里的式子,多看几遍,多推几遍就懂了。
那么我们看到一个东西:\(b_{i} = dp_{i} - sum_{i}^{2}\),而 \(sum_{i}^{2}\) 对于正在考虑的“固定”的 \(i\) 是不变的,那么就可得:截距越小,决策更优(在有些题里是更大更优)。而 \(k_{i}\) 也是不变的,那么就相当于:在平面直角坐标系里点了许多个点,第 \(j\) 个点的坐标是 \((x_{j},y_{j})\),在编号属于 \([1,i)\) 的点里面找一个点 \(j\),使得经过它的斜率为 \(k_{i}\) 的直线截距最小。就像这样:
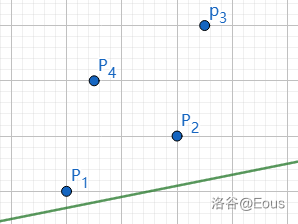
想象这条绿色的线在一直向上移动,它碰到的第一个点就是最优决策点。用盯真法,这里就是 \(P_{1}\)。但是程序不会盯真,所以我们还得想想怎么让程序也会找最优点。很显然,最优点一定在下凸壳(有些是上凸壳)上。于是我们可以用单调栈维护一个凸壳。但是凸壳有了,那凸壳上还有那么多点啊,到底是哪一个呢?
在这幅图里,很显然是最低点 \(P_{1}\),那会不会有其他的情况呢,比如我们把这条线的斜率加大一点:

那现在就不是简单的最低点了,而是 \(P_{2}\)。但是,我们发现,\(P_{1}\) 之所以不是最优解,是因为 \(P_{1}P_{2}\) 这条线的斜率没有绿线大,导致 \(P_{2}\) 先遇到绿线,\(P_{1}\) 和前面的点(如果有的话)就都不会是最优决策点了。于是,我们可以把单调栈换成单调队列,然后在队尾,如果这个点与下一个点的连线比当前斜率 \(k_{i}\) 要小(有些题是大),那么就把他扔出去,扔完之后的队尾就是最优决策点啦。因为每个点至多进出队列一次,所以时间复杂度为 \(\mathcal{O}(n)\)。
当然,还有一种做法,就是继续用单调栈,因为我们维护的是一个凸壳,所以斜率是具有单调性的,我们可以在单调栈上二分出第一个斜率大于等于当前斜率 \(k_{i}\) 的第一个点就是最优决策点,时间复杂度 \(\mathcal{O}(n \log n)\),没有单调队列做法优。
放一下代码:
#include<bits/extc++.h>
#define sq(x) ((x) * (x))
#define int long long
typedef long double ld;
using namespace std;
const int maxn = 5e4 + 5;
int n,l;
int c[maxn],sum[maxn],dp[maxn];
int q[maxn],head,tail;
ld x(int i){return sum[i];}//上文里的x[i]
ld y(int i){return dp[i] + sq(sum[i] + l);}//y[i]
ld k(int i){return (ld)2 * sum[i];}//k[i]
ld slope(int i,int j){return (y(j) - y(i)) / (x(j) - x(i));}
signed main()
{
scanf("%lld%lld",&n,&l);
l++;
for (int i = 1; i <= n; i++)
{
scanf("%lld",c + i);
sum[i] = sum[i - 1] + c[i] + 1;
}
head = 1,tail = 0;
q[++tail] = 0;
for (int i = 1; i <= n; i++)
{
while (head < tail && slope(q[head],q[head + 1]) <= k(i))
head++;//将与下一个点的连线斜率小于等于当前k[i]的扔出去
dp[i] = dp[q[head]] + sq(sum[i] - sum[q[head]] - l);
while (head < tail && slope(q[tail - 1],q[tail]) >= slope(q[tail - 1],i))
tail--;//维护凸壳
q[++tail] = i;//压进队列
}
printf("%lld",dp[n]);
return 0;
}
你肯定注意到了“有些题”和这个题不一样,至于为什么不一样呢?因为有些题的 \(k_{i}\) 是单减的,所以是上凸壳,有些甚至没有单调性,那么我们就要用平衡树或者李超线段树来维护了。单调队列和单调栈只能用于维护横坐标和斜率都单调的方程。
例题 2:P4655 [CEOI2017] Building Bridges
这道题的斜率和横坐标就不单调了。
依旧是先列出朴素的方程:
其中 \(w\) 是预处理好的前缀和。
接下来我们把它化简,并写出 \(l,b,x,y\):
写出 \(l,b,x,y\):
但是我们发现:\(x\) 和 \(k\) 现在都不单调了,所以单调栈和单调队列立即发生爆炸。这时,我们就得请出李超线段树了。
板子这里就不说了。如果用李超线段树的话,\(l,x,b,y\) 略有不同:
具体来说,就是把方程从 \(b = y - kx\) 变成 \(y = kx + b\),经过移项得到 \(dp_{i} = kx + b + \text{something}\)。这里的 \(\text{something}\) 通常是固定的,所以我们可得 \(kx + b\) 最小的是最优决策。那么我们就可以用李超线段树维护线段,查询横坐标为 \(x_{i}\) 时最小的纵坐标。
放一下代码:
#include<bits/extc++.h>
#define int long long
#define sq(x) ((x) * (x))
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int maxn = 1e5 + 5;
int n,cnt,rt;
int h[maxn],w[maxn],dp[maxn];
int k(int j){return -2 * h[j];}
int x(int i){return h[i];}
int b(int j){return dp[j] - w[j] + sq(h[j]);}
struct line
{
int l,b;
line(int k = 0,int b = 0):k(k),b(b){};
int f(int x){return k * x + b;}
};
struct Nahida
{
int ls,rs;
line ln;
bool fl;
}tree[maxn << 2];
void upd(line ln,int l,int r,int &rt)
{
if (!rt)
rt = ++cnt;
int lpos = tree[rt].ln.f(l),rpos = tree[rt].ln.f(r);
int lque = ln.f(l),rque = ln.f(r);
if (!tree[rt].fl)
{
tree[rt].ln = ln;
tree[rt].fl = 1;
return;
}
else if (lque <= lpos && rque <= rpos)
tree[rt].ln = ln;
else if (lque < lpos || rque < rpos)
{
int mid = (l + r) >> 1;
if (ln.f(mid) < tree[rt].ln.f(mid))
swap(ln,tree[rt].ln);
if (ln.f(l) < tree[rt].ln.f(l))
upd(ln,l,mid,tree[rt].ls);
else
upd(ln,mid + 1,r,tree[rt].rs);
}
}
int que(int pos,int l,int r,int rt)
{
if (!rt)
return inf;
int ret = tree[rt].ln.f(pos);
if (l == r)
return ret;
int mid = (l + r) >> 1;
int tmp;
if (pos <= mid)
tmp = que(pos,l,mid,tree[rt].ls);
else
tmp = que(pos,mid + 1,r,tree[rt].rs);
ret = min(ret,tmp);
return ret;
}
signed main()
{
scanf("%lld",&n);
for (int i = 1; i <= n; i++)
scanf("%lld",h + i);
for (int i = 1; i <= n; i++)
{
scanf("%lld",w + i);
w[i] += w[i - 1];
}
upd(line(k(1),b(1)),0,2e6,rt);//初始状态为dp[1]
for (int i = 2; i <= n; i++)
{
dp[i] = que(x(i),0,2e6,rt) + w[i - 1] + sq(h[i]);//查询最小纵坐标
upd(line(k(i),b(i)),0,2e6,rt);//加入线段树
}
printf("%lld",dp[n]);
return 0;
}
例题 3:P4072 [SDOI2016] 征途
这题比较特殊,他的 dp 方程是二维的。我们还是先把朴素的方程写出来。设 \(dp_{i,j}\) 表示到第 \(i\) 走完 \(i\) 条路用了 \(j\) 天的最小方差。那么有:
那么问题就在于如何求贡献,我们先把方差的式子列出来:
其中 \(len_{i}\) 表示第 \(i\) 天走的距离,\(sum\) 表示到目的地的总距离。
现在按照题意,把 \(v\) 乘上一个 \(m^{2}\):
那现在我们就知道每一段的贡献是 \(m \times len_{i}^{2} - 2m \times len_{i} \times sum\)。如此,我们的答案就是 \(dp_{n,m} + sum^{2}\)。记录 \(dis\) 为距离的前缀和,用 \(dis\) 里的数替换 \(len_{i}\) 和 \(sum\),并把完整的 dp 方程写出来:
接下来,我们尝试将它化简:
并尝试写出单调队列形式的 \(k,x,b,y\):
我们发现他的斜率单调递增,可以用单调队列来维护。那具体怎么做呢?我们最外层枚举 \(j\),对于每一个 \(j\) 对应的那一层,我们单独用一个单调队列维护,每层转移开始时清空并重新扔一个新的起始状态进去。
为什么要每层都用一个单独的单调队列?
因为每一层都是独立的,相当于重新开始了一次 dp。
更多细节会在代码里说明:
#include<bits/extc++.h>
#define int long long
#define sq(x) ((x) * (x))
using namespace std;
typedef long double ld;
const int maxn = 3005;
int n,m;
int dis[maxn];
int dp[maxn][maxn];
int q[maxn],head,tail;
//上文里的三哥俩
int k(int i){return 2 * m * dis[i];}
int x(int k){return dis[k];}
int y(int k,int j){return dp[k][j - 1] + m * sq(dis[k]) + 2 * dis[k] * dis[n];}
ld slope(int i,int k,int j){return ((ld)y(k,j) - (ld)y(i,j)) / ((ld)x(k) - (ld)x(i));}
signed main()
{
scanf("%lld%lld",&n,&m);
for (int i = 1; i <= n; i++)
{
scanf("%lld",dis + i);
dis[i] += dis[i - 1];
}
memset(dp,0x3f,sizeof dp);
dp[0][0] = 0;
for (int j = 1; j <= m; j++)
{
//重中之重
head = tail = 1;
q[1] = j - 1;
//因为前 j - 1 天至多走 j - 1 条路,所以初始的就是 j - 1
for (int i = j; i <= n; i++)
{
while (tail > head && slope(q[head],q[head + 1],j) < k(i))
head++;//维护凸壳
int k = q[head];//本来以为会和上面的k(i)冲突的,但是实际上没有
dp[i][j] = dp[k][j - 1] + m * sq(dis[i] - dis[k]) - 2 * (dis[i] - dis[k]) * dis[n];
while (tail > head && slope(q[tail - 1],q[tail],j) > slope(q[tail],i,j))
tail--;//加入队列
q[++tail] = i;
}
}
printf("%lld",dp[n][m] + sq(dis[n]));//输出答案
return 0;
}
例题 4:P5308 [COCI2018-2019#4] Akvizna
这题要用一个叫 wqs 二分的东西。
依然先写出来朴素的 dp 方程。设 \(dp_{k,i}\) 表示在前 \(k\) 轮总共干了 \(i\) 个人,那么有转移:
然后化简:
写出 \(k,x,b,y\)
然后看到 \(k\) 和 \(x\) 都单调,兴致勃勃的开始斜率优化。蛋柿,我们发现优化完了还是有 \(\mathcal{O}(nk)\) 的复杂度,立即发生爆炸。这时候,就得请我们的 wqs 二分登场了。
wqs 二分通常用于求解“正好取 \(k\) 组”的问题,能用它求解的问题通常还有一个特点:如果没有正好取 \(k\) 的要求可以变成一维 dp。我们看,这道题正好满足条件。但是,wqs 二分还有一个要求,就是:设 \(\operatorname{f}(k)\) 为正好取 \(k\) 组的最优解,那么 \(\operatorname{f}\) 是 \(k\) 的凸函数(上凸下凸都可以)。证明的话,打表就可以。我们把每一个横坐标为整数 \(k\),纵坐标为 \(\operatorname{f}(k)\) 的每一个点都画出来:
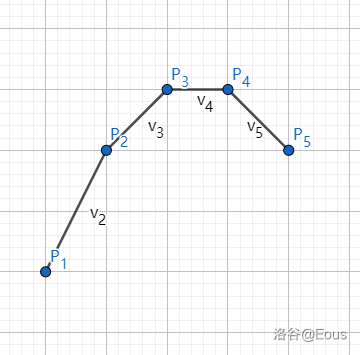
因为凸壳的斜率具有单调性,所以我们尝试二分斜率。用二分到的斜率 \(p\) 去切这个凸壳:
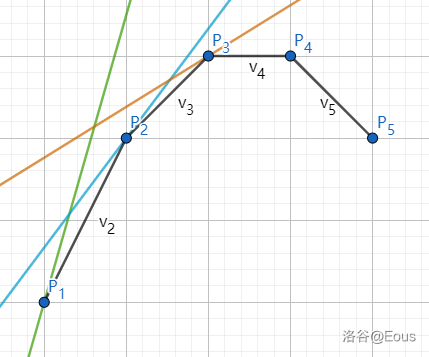
这时的截距就是 \(ans - p \times k\)(这里的 \(k\) 是横坐标)。因为会有 \(k\) 次转移,所以我们在转移的时候,每次减去斜率 \(p\),最终就会得到 \(k\) 时截距 \(b\),也就对应 \(ans\) 最大值。并计算转移次数(或者叫分了几段)。因为斜率越大,切点越高,横坐标也就越大,分的段数也就越多,所以我们在 check 里面打斜率优化 dp,如果转移次数(分的段数)大于 \(k\),那么就说明斜率太小了(结合图片理解),反之就是斜率太大了。
看看代码也许更加懂一些?
#include<bits/extc++.h>
using namespace std;
typedef long double ld;
const int maxn = 1e5 + 5;
const ld eps = 1e-15;
int tot,n;//这里的 tot 是题目中的 k
int q[maxn],head,tail;
ld dp[maxn],g[maxn];
inline ld x(int i){return (ld)1 / ld(n - i);}
inline ld y(int i){return (ld)dp[i] - (ld)i / ld(n - i);}
inline ld k(int i){return (ld)-i;}
inline ld slope(int i,int j){return (y(j) - y(i)) / (x(j) - x(i));}
bool check(ld mid)
{
q[head = tail = 1] = 0;
for (int i = 1; i <= n; i++)//check 里的斜率优化
{
while (head < tail && slope(q[head],q[head + 1]) - k(i) > -eps)//维护凸壳
head++;
int j = q[head];
dp[i] = dp[j] + ld(i - j) / ld(n - j) - mid;
g[i] = g[j] + 1;//记录转移次数(分的段数)
while (head < tail && slope(q[tail],i) - slope(q[tail - 1],q[tail]) > -eps)
tail--;
q[++tail] = i;
}
return g[n] >= tot;//如果分的段数大于k,那么就说明斜率太小了。
}
int main()
{
scanf("%d%d",&n,&tot);
ld l = 0,r = 2e6,mid;
while (r - l > eps && (ld)clock() / (ld)CLOCKS_PER_SEC < 0.9)
{
mid = (l + r) / (ld)2;
if (check(mid))
l = mid + eps;//斜率太小就加
else
r = mid - eps;//太大就减
}
check(l);
printf("%.9Lf",dp[n] + 1.0 * l * tot);
return 0;
}
总结
- 先将 dp 方程化简,尝试写单调队列形式的 \(b = y - kx\):只与 \(i\) 有关的项是 \(b\),只与 \(j\) 有关的项是 \(y\),与 \(i,j\) 都有关的项,分成两半:只与 \(i\) 有关是 \(k\),只与 \(j\) 有关的是 \(x\)。
- 判断单调性。如果 \(k,x\) 有一个不是单调的,那么就不能用单调队列维护凸包,推荐使用李超线段树,因为李超线段树不用任何单调性,而平衡树和 cdq 分治都有单调性的要求,时间复杂度也就多一个 \(\log n\)。
- 如果使用单调队列,那么队首就是最优决策点,用方程转移即可。
- 如果使用李超线段树,那么需要将 \(k\) 和 \(x\) 交换,\(b\) 和 \(y\) 交换,变成 \(y = kx + b\),\(x\) 与 \(i\) 有关,\(b\) 与 \(j\) 有关。转移时,用李超线段树查询 \(i\) 对应的 \(x\) 的纵坐标的最小(最大值),也就是查询 \(x = x_{i}\) 这条线与哪条插入的线段的交点纵坐标最大,为多少。那么查出来的最小(大)纵坐标就对应最优的决策值(\(y = kx + b\)),转移即可。
好题推荐
P3628 [APIO2010] 特别行动队
P5785 [SDOI2012] 任务安排
P2120 [ZJOI2007] 仓库建设
P4360 [CEOI2004] 锯木厂选址
如果有不严谨的地方,欢迎指出。
本文来自博客园,使用 CC BY-NC-SA 4.0 协议。
作者:伊埃斯,转载请注明原文链接:https://www.cnblogs.com/Eous/articles/18658997



 浙公网安备 33010602011771号
浙公网安备 33010602011771号