P2822 [NOIP 2016 提高组] 组合数问题

P2822 [NOIP 2016 提高组] 组合数问题

题目背景

NOIP2016 提高组 D2T1

题目描述

组合数 \(\binom{n}{m}\) 表示的是从 \(n\) 个物品中选出 \(m\) 个物品的方案数。举个例子，从 \((1,2,3)\) 三个物品中选择两个物品可以有 \((1,2),(1,3),(2,3)\) 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 \(\binom{n}{m}\) 的一般公式：

\[\binom{n}{m}=\frac{n!}{m!(n-m)!} \]

其中 \(n!=1\times2\times\cdots\times n\)；特别地，定义 \(0!=1\)。

小葱想知道如果给定 \(n,m\) 和 \(k\)，对于所有的 \(0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )\) 有多少对 \((i,j)\) 满足 \(k\mid\binom{i}{j}\)。

输入格式

第一行有两个整数 \(t,k\)，其中 \(t\) 代表该测试点总共有多少组测试数据，\(k\) 的意义见问题描述。

接下来 \(t\) 行每行两个整数 \(n,m\)，其中 \(n,m\) 的意义见问题描述。

输出格式

共 \(t\) 行，每行一个整数代表所有的 \(0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )\) 中有多少对 \((i,j)\) 满足 \(k\mid\binom{i}{j}\)。

输入输出样例 #1

输入 #1

1 2
3 3

输出 #1

1

输入输出样例 #2

输入 #2

2 5
4 5
6 7

输出 #2

0
7

说明/提示

【样例1说明】

在所有可能的情况中，只有 \(\binom{2}{1} = 2\) 一种情况是 \(2\) 的倍数。

【子任务】

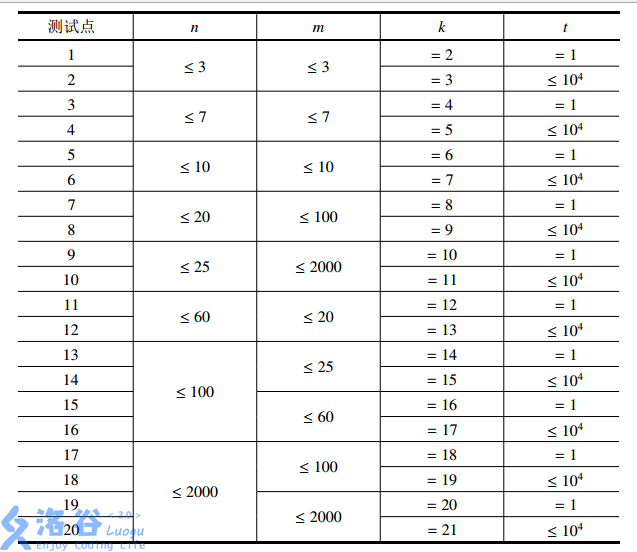
• 对于全部的测试点，保证 \(0 \leq n, m \leq 2 \times 10^3\)，\(1 \leq t \leq 10^4\)。

---

由于本题 \(0 \leq n, m \leq 2 \times 10^3\) ，所以可以用杨辉三角来计算组合数，并及时对 \(k\) 取模，然后用二维前缀和优化查询。
杨辉三角的递推方程式：
\(c_{i,j}=c_{i-1,j-1}+c_{i-1,j}\)

代码如下：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e3+5;
int t,k,x,y,a[N][N];
ll c[N][N];
int main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	memset(c,-1,sizeof(c));
        //把c数组全部设置成-1。因为计算过的c[i][j]如果是0，说明C(i,j)是k的倍数，但没计算到的c[i][j]默认为0，会跟计算过的c[i][j]混淆
	cin>>t>>k;
	c[0][0]=1;
	for(int i=1;i<=2000;i++){
		for(int j=0;j<=i;j++){
			if(j==0||j==i)c[i][j]=1;
			else c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;
		}
	}//用杨辉三角计算组合数
	for(int i=0;i<=2000;i++){
		for(int j=0;j<=2000;j++){
			a[i][j]=(c[i][j]==0);
			if(i)a[i][j]+=a[i-1][j];
			if(j)a[i][j]+=a[i][j-1];
			if(i&&j)a[i][j]-=a[i-1][j-1];
		}
	}//二维前缀和
	while(t--){
		cin>>x>>y;
		cout<<a[x][y]<<'\n';
	}
	return 0;
}