R画ROC曲线

　　学了一下ROC图形的原理，在此实现一下，算是理论落地的训练，只不过目前看的是二分类问题。

• FPR、TPR简介　　

　　ROC曲线的横坐标为FPR，叫做假正例率，也就是实际为假的观测中被判断为真的所占的比例。

　　ROC曲线的纵坐标为TPR，叫做真正例率，也就是实际为真的观测中被判断为真的所占的比例。

　　举例如下：

表1

实际分类	判定分类
P	P
P	N
N	P
P	N
N	N

此例中，实际为假的观测(N:negative)共2个，其中被判定为真的有1个，因此FPR=1/2=0.5；实际为真的观测(P:positive)共3个，其中被判定为真的有1个，因此TPR=1/3。

• ROC绘制过程

　　但是实际的二分类问题往往给出的是判定为真的概率，也就是如下的表格：

表2

实际分类	判定为真的概率
P	0.9
P	0.6
N	0.5
P	0.4
N	0.3

　　如果你认为判定为真的概率不小于0.9，就能认为该观测为真，那么表2更新如下：

表3

实际分类	判定分类
P	P
P	N
N	N
P	N
N	N

于是得到一个坐标(FPR,TPR)=(0/2,1/3)=(0,1/3)。

　　如果你认为判定为真的概率不小于0.6，就能认为该观测为真，那么表2更新如下：

表4

实际分类	判定分类
P	P
P	P
N	N
P	N
N	N

于是得到一个坐标(FPR,TPR)=(0/2,2/3)=(0,2/3)。

　　以此类推，即以“判定为真的概率”中的各个概率p为临界值，如果概率不小于p，则判定为真，否则为假。按照这条规则对表2进行更新，最终可以得到如下表格：

表5

实际分类	判定为真的概率	FPR	TPR
P	0.9	0	1/3
P	0.6	0	2/3
N	0.5	1/2	2/3
P	0.4	1/2	3/3
N	0.3	2/2	3/3

　　得到上面这5个点之后就可以画图了，一般来讲ROC图都是锯齿图，且图形越靠近左上角说明分类器准确率越高，越接近斜率为1的对角线说明分类器性能越差。

• R代码实现

　　理解了上面的原理，画图也简单了，关键在于表2的更新如何实现，推荐的方法是先对判定为真的概率进行一个从大到小的排序。为了便于使用，这里直接定义一个函数进行封装。

ROC_Plot<-function(real_category,probs,positive_symbol,...){
      real<-ifelse(real_category==positive_symbol,"P","N")
      rows<-length(real)
      ROC<-matrix(NA,ncol=2,nrow=rows)
      colnames(ROC)<-c("FPR","TPR")

      for(i in 1:rows){
            DF<-data.frame(real=real,predict=c(rep("P",i),rep("N",rows-i)))
            DF_N<-subset(DF,real=="N")
            ROC[i,1]<-sum(DF_N$predict=="P")/nrow(DF_N)

            DF_P<-subset(DF,real=="P")
            ROC[i,2]<-sum(DF_P$predict=="P")/nrow(DF_P)
      }
      with(as.data.frame(ROC),
      {plot(FPR,TPR,xlim=c(0,1),ylim=c(0,1),...)
      abline(a=0,b=1,lty='dotted')})
}

 　　函数ROC_Plot的real_category是实际分类向量，probs是对应的判定为真的概率的向量，positive_symbol是观测为真的标志，'...'是省略的画图参数，这是需要自己加的。

　　直接调用该函数完成表2的ROC图绘制：

ROC_Plot(real_category=c('p','p','n','p','n'),
         probs=c(0.9,0.6,0.5,0.4,0.3),
         positive_symbol='p',
         type="l",col="red",
         xlab="假正例率(FPR)",ylab="真正例率(TPR)",main="ROC")

 图形如下：

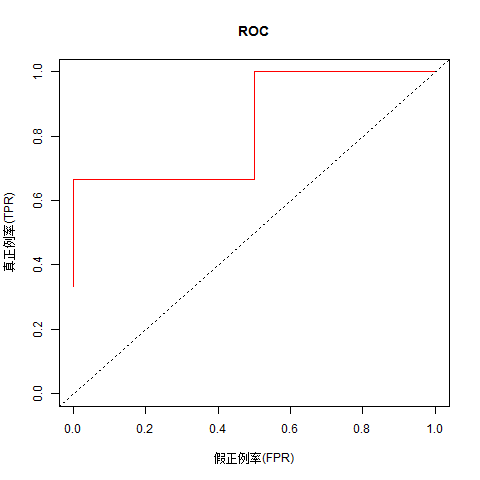
　　更多观测也可以直接套用该函数，在此只给代码示例，图形就不放了。

ROC_Plot(
      real_category=
      c('p','p','n','p','p',
        'p','n','n','p','n',
        'p','n','p','n','n',
        'n','p','n','p','n'),
      probs=
      c(.9,.8,.7,.6,.55,
        .54,.53,.52,.51,.505,
        .4,.39,.38,.37,.36,
        .35,.34,.33,.30,.1),
      positive_symbol="p",
      type="l",
      col="red",
      xlab="假正例率(FPR)",
      ylab="真正例率(TPR)",
      main="ROC")