科学发现：现象 vs 可能的解释模型 --> 不同领域知识的共享表征空间、一致性约束

把科学发现粗略抽象成一个问题：。

• 我们面对一堆现象（观测、实验、经验规律）。
• 我们想找一个模型/理论来解释并预测它们。
• 但“所有可能模型”太多，几乎无限。

真正的瓶颈常常不是“没有模型”，而是“模型空间太大”。跨域突破的高杠杆做法，不是盲目扩大搜索，而是：

• 先选择一个更统一的表示，把原本分离的领域对象都映射进去；
• 然后把在该表示中天然成立的硬约束（对称性、守恒、可组合、因果、可测量性等）变成筛子；
• 让筛子不断把候选理论空间筛小，直到剩下少数结构稳定的家族。

因此，新理论很多时候不是被随意“发明”出来，而是被一致性要求“逼”出来。

1. 把两个领域放进同一表征空间（例如：把引力写成几何；把热力学写成统计；把遗传写成信息与化学反应网络）。
2. 在这个共享表征里施加一致性约束（对称性、守恒、可微性、可测量性、因果结构），从而大幅缩小“可能理论”的搜索空间。
3. 结果是：可行理论空间被急剧压缩，某些结构几乎被“逼迫”出现——这往往就是新理论的核心。

这意味着：真正产生新理论的，不只是“知识更多”，而是能否对不同领域的知识强制进行共享表征空间、一致性约束。本文将详细说明。

 

1. 什么是“共享表征空间”？

表征空间可以理解为：你用什么语言、对象、结构去描述世界。

• 在经典力学里，你用位置、速度、力、能量；
• 在几何里，你用流形、度量、曲率、联络；
• 在统计物理里，你用微观态、分布、熵、配分函数；
• 在信息论里，你用编码、互信息、复杂度、压缩。

所谓“把两个领域放进同一表征空间”，不是把术语硬翻译，而是找到一种表示，使得：

• 领域A的核心对象能自然嵌入；
• 领域B的核心对象也能自然嵌入；
• 更关键的是：两边的关键操作（推导、变换、组合、取极限）可以在这个空间里统一表达和相互翻译。

1.1 三种常见的统一方式

（1）对象统一：把“实体”对齐成同类对象
例子：把“引力”从一种力的描述，迁移为时空几何结构（度量/曲率）；把“温度/压强”等宏观量迁移为微观分布的统计性质。

（2）变换统一：把“对称/不变性”提升为第一原则
与其先写方程，不如先规定允许的变换群（坐标变换、规范变换等），然后要求规律在变换下保持不变/协变，很多结构就被迫出现。

（3）优化统一：把“规律”改写成极值原理
最小作用量、最大熵、最小自由能等，把看似不同的规律统一成“在某个函数空间里找极值”的问题，从而共享同一套变分工具链。

 

共享表征空间只是“能放到一起”，还不够。你还需要对齐：让两边的概念关系在新空间里真正对应起来。

结构对齐至少包含三层：

1）语义对齐：这两个量在解释上指向同一类东西吗？
2）操作对齐：对它们做同一种操作（组合、微分、取极限、变换）时，行为一致吗？
3）约束对齐：它们各自必须满足的限制，能否在新空间里用同一套规则表达？

1.2 “类比”是开始

很多跨域工作从类比开始：热像信息、电像流体、学习像压缩……
类比的价值在于提供一个候选映射，但类比本身不保证正确。类比升级为理论，需要两件事：

• 能在共享表征里写出清晰、可推导的对应关系；
• 能通过一致性约束推导出新结论，最好是可证伪预测。

2. 什么是“一致性约束”？

在共享表征里，一致性约束的意思是：

你在系统的一部分施加约束，这些约束通过结构关系传递到其它部分，从而强迫整体形状收缩。

换句话说：约束不是一条条孤立的条件，而是会“连锁反应”的。你一旦接受某个表示和若干硬约束，很多自由度会自动消失。

2.1 约束从哪里来？

常见的“硬约束”来源包括：

• 对称性/协变性：规律不应依赖你怎么选坐标系、基准或描述方式；
• 守恒律：能量、动量、电荷等（常与对称性深度相关）；
• 局部性与可微性：相互作用不能任意非局部；变化应当是可微/连续或满足特定正则性；
• 因果结构：信息传播受限，未来不能影响过去；
• 可测量性/可识别性：理论对象必须能映射到可观测量，参数必须能被数据区分；
• 可组合性：两个系统拼在一起，理论应能自然组合（这会强烈约束形式）；
• 一致性/无矛盾：不同推导路径应导出同一结果（很多“闭合条件”“交换图”都来自这里）。

这些约束在旧表征里可能隐含、分散、难用；在新表征里可能变得简单、可计算、可传播。

2.2 约束如何“缩小理论空间”？

可以把理论空间想象为一个巨大集合，里面装着所有候选模型。约束传播相当于不断取交集：

• 先满足已知观测：留下能解释旧事实的模型；
• 加入对称性：砍掉一大片；
• 加入局部性、因果性：再砍；
• 加入可测量性与可组合性：继续砍；
• 最后剩下少数结构稳定的家族，甚至只剩一个。

很多大理论之所以“像是自然长出来的”，就是因为强约束把选择空间压得太小了。

 

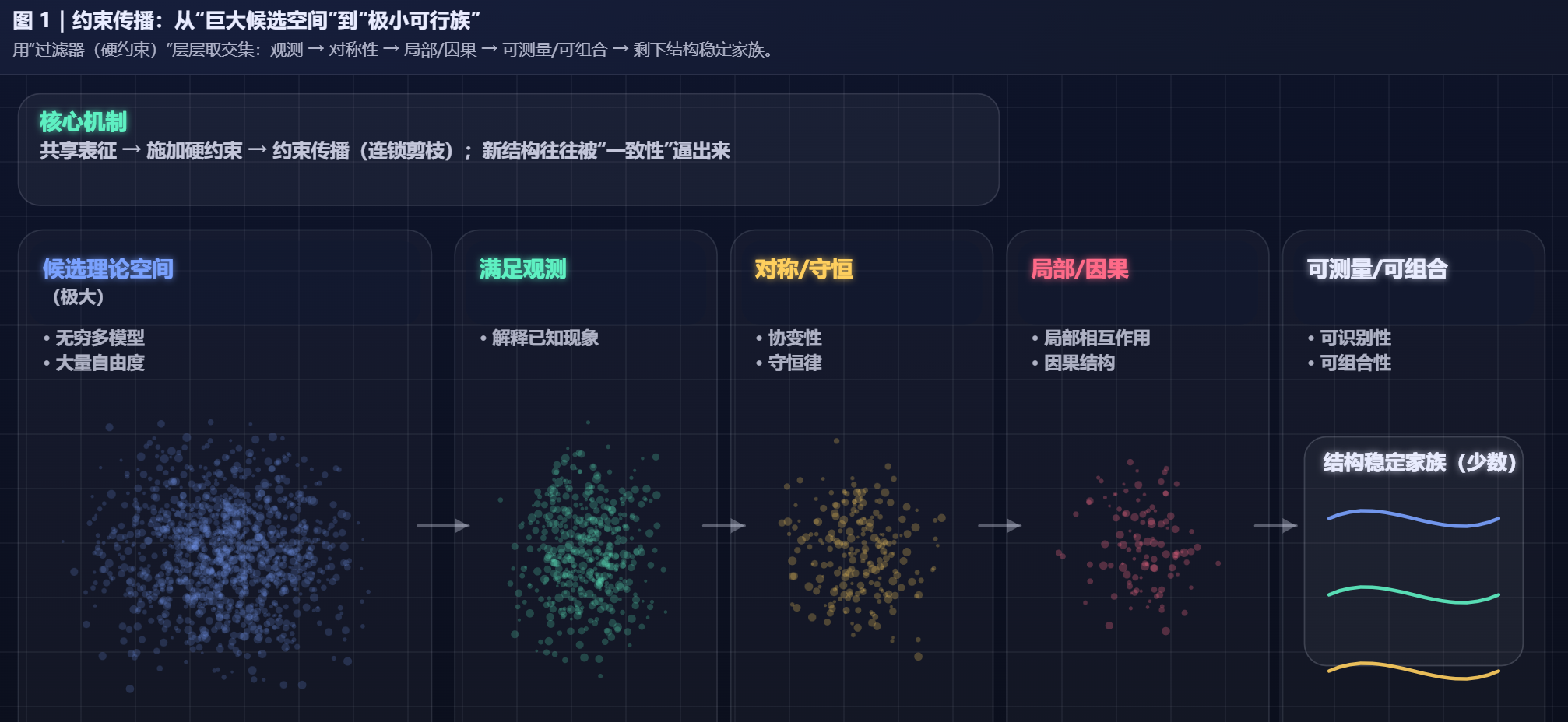
2.3 施加一致性约束，大幅缩小搜索空间

把两个领域放在一起后，最神奇的事情发生了：原本在各自领域里看起来“可以随意设定”的参数，现在变得“不得不这样”。 这就是约束传播。

在科学理论的探索中，“可能性的空间”是无限大的。如果你只是瞎猜，永远猜不到正确的理论。但是，当你要求新理论必须同时满足两个领域的硬性规则时，可能性的空间就会从“无限大”坍缩成“极小的一点”。

1. 对称性约束（Symmetry Constraints）

在物理学中，如果你要求理论必须满足某种对称性（比如洛伦兹不变性，即在任何惯性系下物理定律不变），原本可以随意写的方程就被锁死了。

• 例子： 狄拉克试图将量子力学（波动方程）和狭义相对论（洛伦兹协变性）结合。
• 约束传播： 为了同时满足这两个约束，他发现方程必须是矩阵形式，而且必须存在一种反粒子（正电子）。
• 结果： 他不是“发明”了反物质，而是发现为了保持逻辑一致性，反物质必须存在。

2. 守恒与可微性约束

• 例子：深度学习（神经网络）。
  • 表征： 将图像识别、自然语言处理都映射到高维向量空间（Vector Space）。
  • 约束： 整个系统必须是可微的（Differentiable），以便使用链式法则（Backpropagation）进行优化。
  • 结果： 这一强约束排除了无数种离散的、基于规则的AI算法，迫使我们寻找连续的函数逼近器，最终导致了AI的爆发。

3. 因果结构约束

• 例子：广义相对论中的光锥。
  一旦将引力几何化，时空结构必须保证因果律不被破坏（结果不能先于原因）。这限制了时空弯曲的极限，预言了黑洞视界的存在——视界之内，因果结构与外部断裂。

 真正的理论突破，往往是因为发现“只有这一种数学结构，能同时满足所有的约束条件”。这就像拼图，当你把周围的边界（约束）都拼好后，中间那块拼图的形状就被唯一确定了。

3. 几个典型范式：统一表征 + 约束逼出结构

3.1. 引力-->几何（广义相对论）

• 旧表征： 牛顿力学中，引力是一种“力”，在平直的欧几里得空间中瞬间传播。
• 冲突： 这与狭义相对论（光速限制）冲突。
• 新表征（几何）： 爱因斯坦不再把引力看作“力”，而是看作时空的弯曲。
• 对齐： 物质（物理量）告诉时空如何弯曲（几何量）；时空（几何量）告诉物质如何运动（物理量）。
• 结果： 物理学问题变成了黎曼几何问题。所有关于曲率、测地线的几何定理，瞬间变成了物理定律。

3.2. 热力学-->统计（统计力学）

• 旧表征： 热力学关注宏观量（温度、压强、熵），是唯象的（知其然不知其所以然）。
• 新表征（概率统计）： 玻尔兹曼认为，宏观只是微观粒子状态的统计分布。
• 对齐： “温度”对齐为“分子平均动能”；“熵”对齐为“微观状态数的对数”（$S=k \ln \Omega$）。
• 结果： 热力学不再是独立的定律，而是牛顿力学在大数定律下的必然结果。两个领域在“概率空间”里统一了。

3.3. 遗传-->信息（分子生物学）

• 旧表征： 生物学关注性状、杂交、表现型。
• 新表征（信息论）： 薛定谔在《生命是什么》中预言遗传物质是“非周期性晶体”，沃森和克里克后来证实了DNA。
• 对齐： 氨基酸序列对齐为“编码”；遗传变异对齐为“信息复制错误”；进化对齐为“算法迭代”。
• 结果： 生命科学从此变成了信息科学。我们可以用处理代码的方式（剪切、复制、粘贴）来处理生命。
  
  未完待续，下一篇：

  通往科学发现的AI还需要什么？