Splay学习笔记

这已经是第三次学习 Splay 了

图片内容转载自 yyb 的博客

二叉搜索树

本来是一颗二叉树，但是满足这样的条件：

对于一个节点 \(x\)， 满足它的左子树中所有节点的 \(val\) 都小于 \(val_x\)，右子树中的所有节点的 \(val\) 都大于 \(val_x\)。

那么很显然，我们最希望它（尽可能）是一颗满二叉树，或者说深度为 \(logn\)，这样可以做到在 \(\Theta(logn)\) 的时间内处理数列信息。

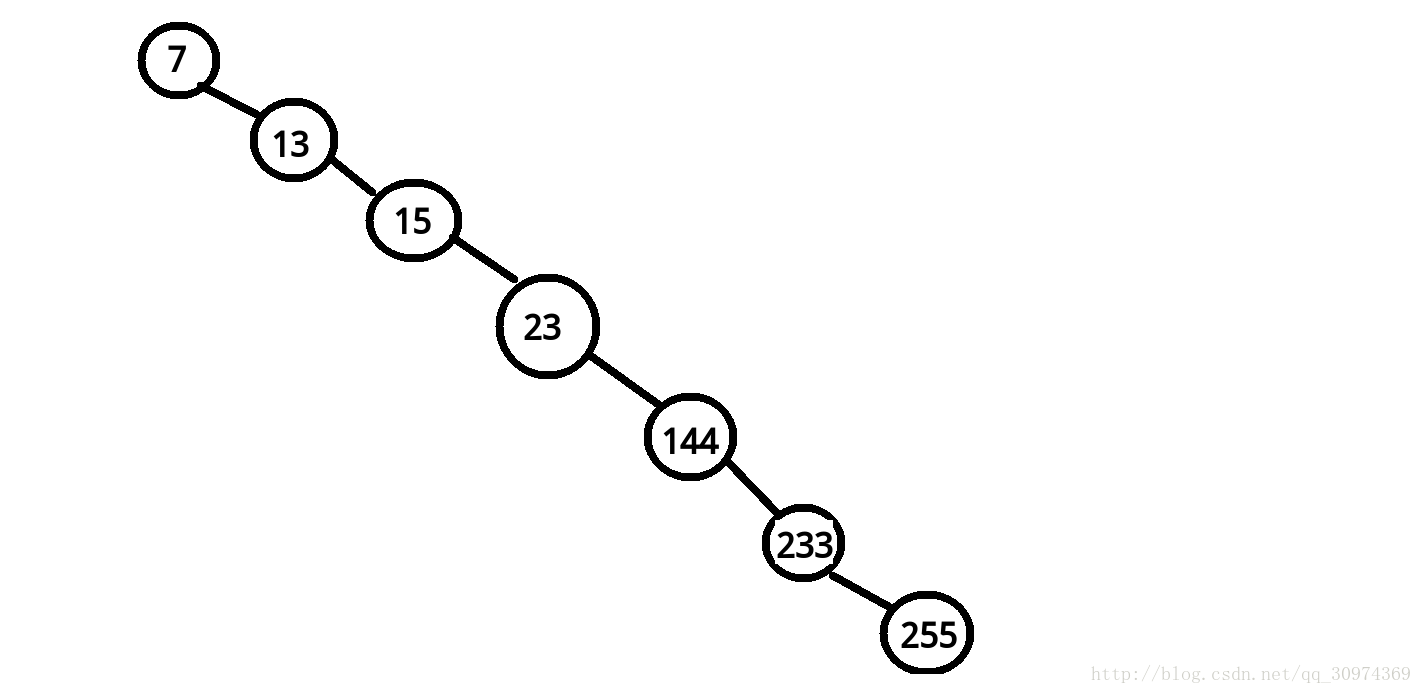
然而在很多时候，如果不加维护，在极端情况下它可能会变成这样：

那么这样我们查询一次就很可能会变成 \(\Theta(n)\)，这是我们不希望看到的。

于是我们就有了很多很多树，来维护这个东西。

Splay

Splay 就是一颗二叉搜索树，或者说一种维护二叉搜索树的方式。

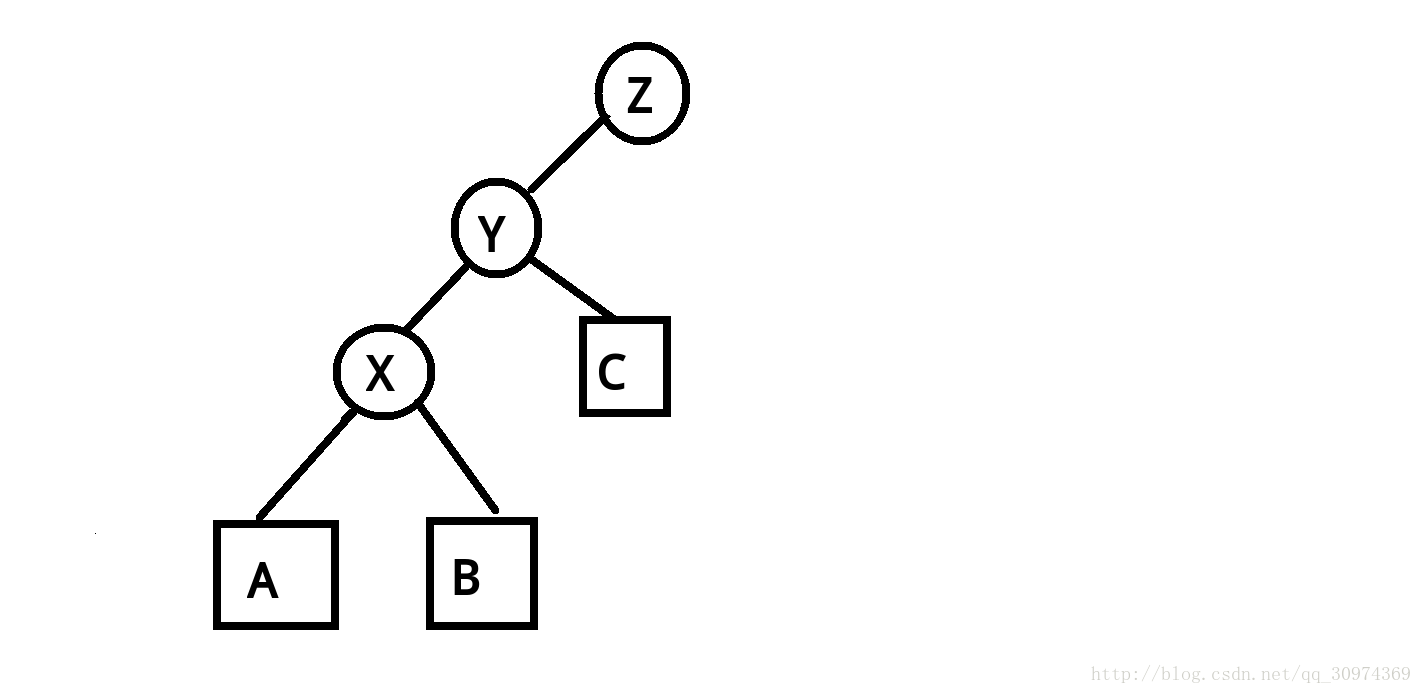
现在有一颗二叉搜索树：

\(X\)、\(Y\)、\(Z\) 都是平衡树上的节点，而 \(A\)、\(B\)、\(C\) 是一整棵子树，显然有：

\[A<X<B<Y<C<Z \]

现在我们想让 \(X\) 到 \(Y\) 的位置去，该怎么办呢？

首先把 \(X\) 直接放在 \(Y\) 的位置，现在 \(Y\) 没有地方去了。

然后因为 \(Y>X\)，再把 \(Y\) 放在 \(X\) 的右儿子（\(B\)）的位置，现在 \(B\) 没有地方去了。

最后因为 \(B<Y\)，所以可以把 \(B\) 放在 \(Y\) 的左儿子上，注意到我们把 \(X\) 拿走了之后，\(Y\) 没有左儿子了，所以现在这棵树的每个点都有了自己的归属。

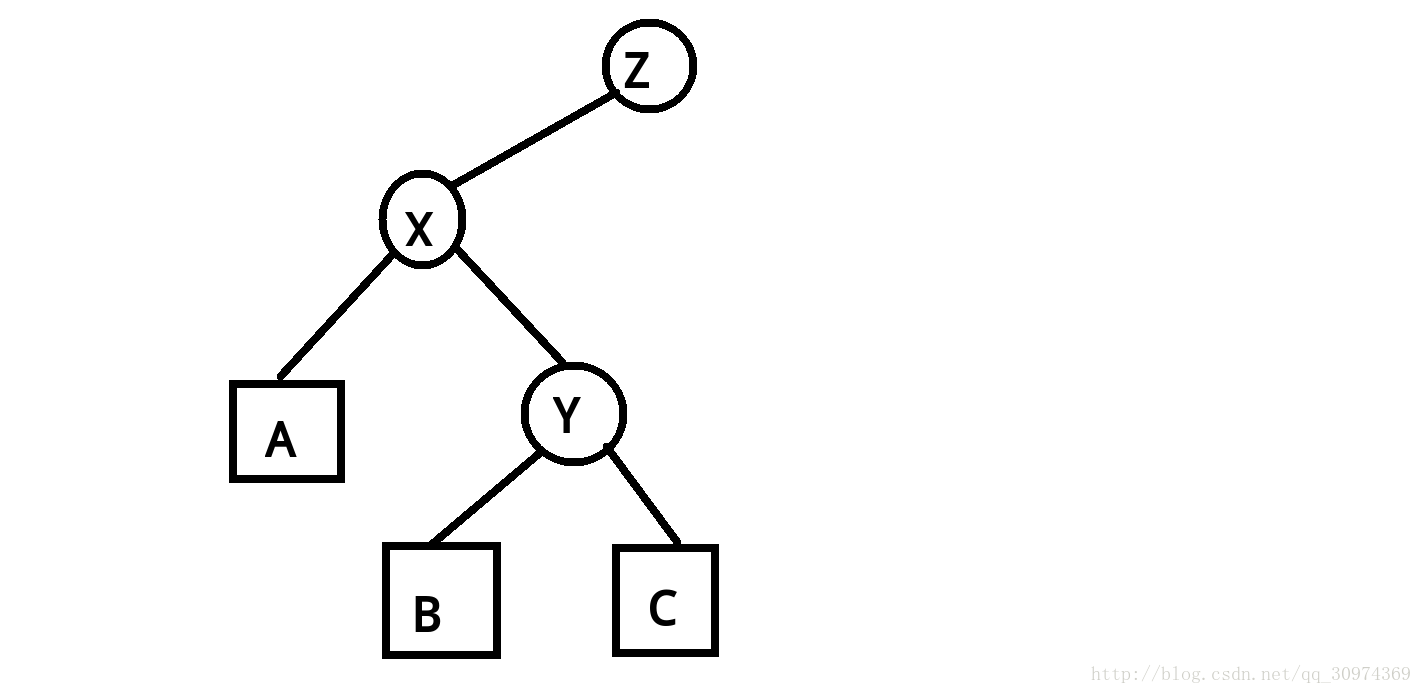
于是这棵树变成了这样：

这就是 rotate 的基本操作，但是这只是一种情况。

现在来分类讨论，一共四种情况：

1. \(X\) 是 \(Y\) 的左儿子，\(Y\) 是 \(Z\) 的左儿子
2. \(X\) 是 \(Y\) 的左儿子，\(Y\) 是 \(Z\) 的右儿子
3. \(X\) 是 \(Y\) 的右儿子，\(Y\) 是 \(Z\) 的左儿子
4. \(X\) 是 \(Y\) 的右儿子，\(Y\) 是 \(Z\) 的右儿子

对于每一种情况，简单转一转可以发现一个普遍的规律，也就是 rotate 的整个过程：

0. 初始化

int y=t[x].fa,z=t[y].fa;
bool flag=(x==t[y].ch[1]);

1. 把 \(X\) 放在 \(Y\) 的位置，现在 \(Y\) 没有地方放了

t[z].ch[y==t[z].ch[1]]=x,t[x].fa=z;

2. 把 \(Y\) 放在 \(X\) 的 \(X\) 对于 \(Y\) 的那个儿子的相对的那个儿子的位置，原来处在那个位置的节点记为 \(t\)

t[x].ch[flag^1]=y,t[y].fa=x;

3. 把 \(t\) 放在 \(Y\) 的 \(X\) 对于 \(Y\) 的那个儿子的位置，那个位置原本属于 \(X\) 而它现在空出来了，可以直接填进去

t[y].ch[flag]=t[x].ch[flag^1];
if(t[x].ch[flag^1])t[t[x].ch[flag^1]].fa=y;//需要注意这里可能 X 根本没有这个儿子

这只是示意代码，但是为了防止需要的信息被提前更新掉，应该把 \(2\)、\(3\) 的位置交换：

inline void rotate(int x)
{
    int y=t[x].fa,z=t[y].fa;
    bool flag=(x==t[y].ch[1]);
    t[z].ch[y==t[z].ch[1]]=x;t[x].fa=z;
    t[y].ch[flag]=t[x].ch[flag^1];
    if(t[x].ch[flag^1])t[t[x].ch[flag^1]].fa=y;
    t[x].ch[flag^1]=y,t[y].fa=x;
    return;
}

然后有了 rotate 操作，我们就可以在保证平衡树结构的前提下，任意改变节点的位置了。

直接说结论：

• 如果 \(X\) 对于 \(Y\) 的儿子的位置与 \(Z\) 对于 \(X\) 的位置不同，则 rotate(x)
• 如果 \(X\) 对于 \(Y\) 的儿子的位置与 \(Z\) 对于 \(X\) 的位置相同，则 rotate(y)

最后再 rotate(x)，直到 \(X\) 到达指定位置，最后如果是改变到根，就要更新根的编号。

inline void splay(int x,int goal)
{
    while(t[x].fa!=goal)
    {
        int y=t[x].fa,z=t[t[x].fa].fa;
        if(z!=goal)(y==t[z].ch[1])^(x==t[y].ch[1])?rotate(x):rotate(y);
        rotate(x);
    }
    if(!goal)root=x;
    return;
}

以上就是 Splay 的核心操作，其他的任何操作都只需要以二叉搜索树为基础，利用其性质进行询问（操作）即可。

insert

根据二叉搜索树的性质，找到这个权值所对应的节点：

如果有这个节点，直接 cnt++,siz++，否则新建一个节点给这个父亲。

inline void insert(int val)
{
    int x=root,fa=0;
    while(val!=t[x].val)
        fa=x,x=t[x].ch[val>t[x].val];
    if(x)t[x].cnt++,t[x].siz++;
    else
    {
        x=++siz;
        node now;
        if(fa)t[fa].ch[val>t[fa].val]=x;
        now.val=val,now.fa=fa;
        now.ch[0]=now.ch[1]=0;
        now.cnt=now.siz=1;
        t.push_back(now);
    }
    splay(x,0);
    return;
}

delete

把要删除的节点 splay 到根。