[Leetcode]40.路径总和 III

题目：

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

 

示例 1：

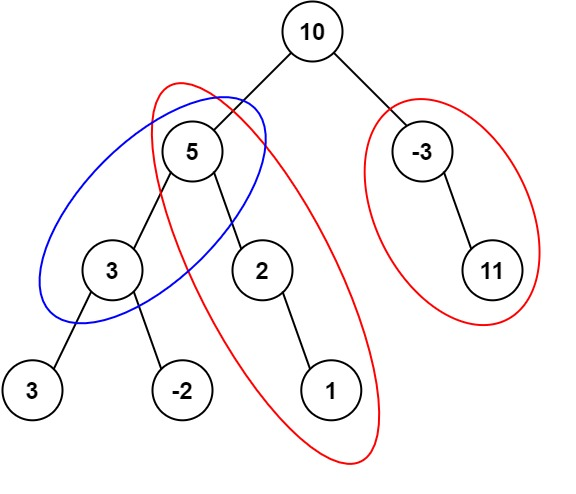
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8

输出：3

解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

 

思想一：两次递归，内层递归是dfs，遍历每个节点的值，计算出从某个结点出发到当前结点的路径和与目标值的差，如果当前结点目前的路径和等于目标值，则将结果+1。考虑到不从根节点出发的情况，我们再对每个节点进行外层，计算从各个结点出发到他们子树的路径和。

func pathSum(root *TreeNode, targetSum int) int {
	var res = 0
	if root == nil{
		return res
	}
	res = dfs3(root,targetSum)  //外层递归 计算从各节点出发 路径和是否等于目标值。
	res += pathSum(root.Left,targetSum)
	res += pathSum(root.Right,targetSum)
	return res
}

func dfs3(node *TreeNode, targetSum int)(res int){  //内层递归 计算从传入结点开始到当前结点的路径和是否等于目标值，如果不登录，递归传入左右子节点与距目标节点的差值。
	if node == nil{
		return 0
	}
	cur := node.Val
	if cur == targetSum{
		res += 1
	}
	res += dfs3(node.Left,targetSum-cur)
	res += dfs3(node.Right,targetSum-cur)
	return res
}

 

思想二：一次递归，增加一个map结构记录当前遍历结点有多少种路径和，比如1-2-3-4，当遍历到4的时候，会将1、3、6、10这四个结果记录进map，如果我们要找4这个目标值，会寻找当前值-目标值，即10-4 =6这个值是否存在，如果存在表示在到达10这个路径和之前存在一个路径和为6，我们可以断开路径和为6的路径，只保留4这个路径达到目标值。这样不用递归每一个结点到当前结点的路径和。

func pathSum(root *TreeNode, targetSum int) int {
	var path = make(map[int]int)  //用来记录打成某个路径和所可能的方式个数
    　　 path[0]=1   //初始化达成0这个路径和的方式有1次 即什么路径都不经过
	return dfs3(root,0,targetSum,path)
}

func dfs3(node *TreeNode,cur int,targetSum int,path map[int]int)int{
	if node ==nil{
		return 0
	}
	cur += node.Val
	cnt:=0  //记录当前可以达成目标数的方式初始化为0次
	if v,ok:= path[cur-targetSum];ok{  //如果找到了前面路径可以通过改变来使得当前路径变成目标值的可能的话，加上这么多种方式
		cnt+=v
	}
 	path[cur]++ //从该节点经过打成cur路径和的方式+1
	cnt += dfs3(node.Left,cur,targetSum,path)
	cnt += dfs3(node.Right,cur,targetSum,path)
	path[cur]-- //当不从该结点经过的时候，要相应把达成这个路径和的方式-1
	return cnt
}

题目来源：https://leetcode-cn.com/problems/path-sum-iii