[Leetcode]34.二叉搜索树中第K小的元素

题目:给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

 

示例 1：

 

 

 
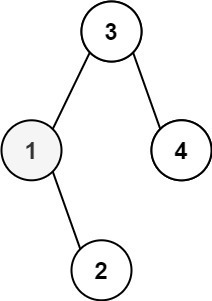
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

 

 

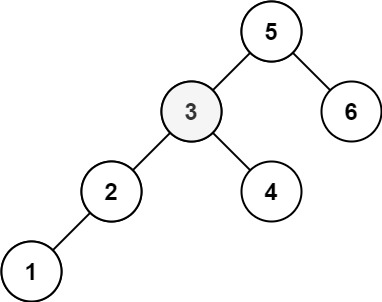
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

 
提示：

    树中的节点数为 n 。
    1 <= k <= n <= 104
    0 <= Node.val <= 104

思想一:

二叉搜索树的中序遍历就是有序的,只需要遍历找到第k个元素即可。

时间复杂度：O(H+k)，其中 H 是树的高度。在开始遍历之前，我们需要 O(H) 到达叶结点。当树是平衡树时，时间复杂度取得最小值 O(log⁡N+k)；当树是线性树（树中每个结点都只有一个子结点或没有子结点）时，时间复杂度取得最大值 O(N+k)。
空间复杂度：O(H)，栈中最多需要存储 H 个元素。当树是平衡树时，空间复杂度取得最小值 O(log⁡N)；当树是线性树时，空间复杂度取得最大值 O(N))。

思路二：

　遍历统计左边子树的结点个数c，根节点是第c+1大的数，如果k==c+1，返回根节点的值，如果k<c+1,那么表示第k大的元素在根节点的左子树上,递归(root.Left,k),如果k>c+1,表示第k大的元素在根节点的右子树上,递归(root.Right,k-1-c),这里要减去左子树的结点个数和根节点的和,表示减去比root.right小的个数。

 

func kthSmallest(root *TreeNode, k int) int {
	var count func(root *TreeNode) int
	count = func(root *TreeNode) int {
		if root != nil {
			return 1 + count(root.Left) + count(root.Right)
		} else {
			return 0
		}
	}
	left := count(root.Left)
	if k == left+1 {
		return root.Val
	} else if k < left+1 {
		return kthSmallest(root.Left, k-1)
	} else {
		return kthSmallest(root.Right, k-1-left)
	}
}

时间复杂度：预处理的时间复杂度为 O(N)，其中 NNN 是树中结点的总数；我们需要遍历树中所有结点来统计以每个结点为根结点的子树的结点数。搜索的时间复杂度为 O(H)，其中 HHH 是树的高度；当树是平衡树时，时间复杂度取得最小值 O(log⁡N)；当树是线性树时，时间复杂度取得最大值 O(N)。

空间复杂度：O(N)，用于存储以每个结点为根结点的子树的结点数。

题目来源：https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst