L1、L2正则化是如何实现权重衰减与减少过拟合的

首先，L1和L2正则化的目的都是减少过拟合，而正则化实际上是通过实现权重衰减而达成减少过拟合的目的的。

我们知道L1和L2正则化可以写成这种形式：

我们在应用正则化的过程中实际上是在梯度下降法优化函数的过程中实现的。我们知道，损失函数可以定义为J（W，b）,其中W是权重参数，b是偏置，一般不作考虑。每次梯度下降后都会对W进行更新，W=W-η·∇_WJ（W），实际就是对损失函数求梯度，用梯度乘学习率然后对原W进行更新。

而我们应用正则化后 可以将上式改写成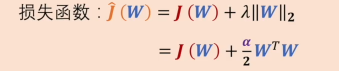，推导过程：

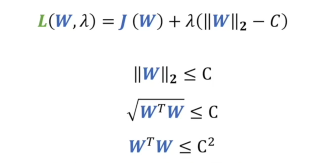这里将L2正则化写成限制形式，对w进行约束，w的L2范数要小于C，展开后即为向量的平方再开方小于C，也就是向量的平方小于C的平方，再换回原式，就相当于用W^TW代替了W的L2范式，将λ替换为a/2方便求导。

而此时对权重进行更新可以得到结果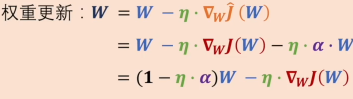，多了一个对正则化项求的梯度，也就是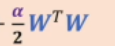的导数×学习率，合并项后得到一个新的权重更新方程，与未正则化的方程W=W-η·∇_WJ（W）对比发现其W的系数每次更新都会减去一个学习率×a的系数，这就是权重衰减的原理。

 

接下来结合理论解释为什么权重衰减可以降低过拟合，用《统计学习方法》给出的案例，我们尝试使用一个方程去拟合一些点。

当我们设定方程的次数为0次时，是一条直线，拟合效果很差，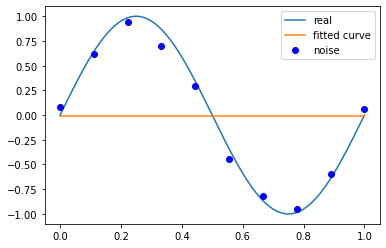

当我们设定方程的次数是1次时，有了系数的影响，拟合效果稍微好了一些，但是还是欠拟合状态。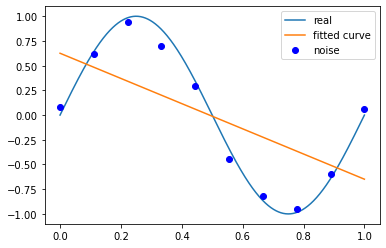

当我们设定方程的次数是3次时，可以看到，拟合效果已经非常好了，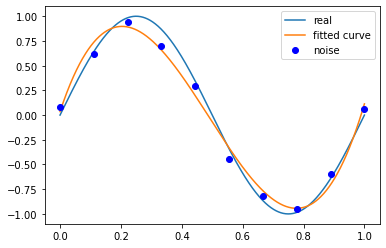

如果我们还想通过提高方程次数来增强拟合能力的话，虽然在训练集上是可行的，但是会影响其泛化能力，进入过拟合状态，在测试集的效果会大大降低。

比如我们将次数设定到9次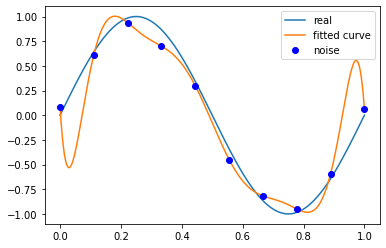，，可以看到如果我们理想曲线就是3次的曲线的话，那么填充3次曲线的点验证9次拟合会发现误差很大。

这就是正则化的用途，正则化通过限定权重来限制高次项的过拟合，假定我们在9次给出的表示方程为：f（x）=ax+bx²+cx³+dx⁴+ex⁵+fx⁶+gx⁷+hx⁸+ix⁹,可以观察到，主要影响我们拟合曲线的是越来越大的高次项，而应用正则化后他会使得高次项前面的权重系数逐渐衰减（1-ηa）w，这个衰减的值会逐步稳定在一个合理的范围，使得曲线降低高次项过拟合的影响。

当然，在实际的学习过程中，我们往往不会出现太过极端的过拟合情况，通常训练到符合某个误差范围或者说是一个最值点就会结束训练，权重衰减也不会一直减少下去。