[主席树]ZOJ2112 && BZOJ1901 Dynamic Rankings
题意:n个数,q个询问 (n<=50000, q<=10000)
Q x y z 代表询问[x, y]区间里的第z小的数
C x y 代表将(从左往右数)第x个数变成y
上篇介绍了在[x, y]区间内查询第z小的数的方法(静态主席树)
本题有更新操作
若仍用上篇的做法,
每次更新一个数,需要更新的是T[i], T[i+1]... ...T[n](该数所在的树以及它后面的所有树)
因为每棵树T[i]所记录的都是前缀(1到i的数出现的次数) 因此,改变i,会影响i到n的所有树
这样,每次更新的复杂度最坏为O($n$),最坏更新q次即为O($n\times m$) 复杂度相当庞大,很明显这样做是不行的
那怎么办呢?
我们可以发现,对于改变i处的数这个操作,对于T[i], T[i+1]... ...T[n]这些树的影响是相同的
都只改变了 “原来i处的数 的数量” 和 “现在i处的数 的数量” 这两个值而已
我们只要在原来的基础上增加一类树, 用它们来维护更新掉的数
即用树状数组来记录更新,每次更新$logn$棵树
下面来演示一下建树到查询的过程:
比如此题的第一个案例
5 3 3 2 1 4 7 Q 1 4 3 C 2 6 Q 2 5 3
先将序列以及要更新的数(C操作)离散化
即3 2 1 4 7 、 6 ---->(排序) ----> 1 2 3 4 6 7
那么我们就需要建一棵这样的树: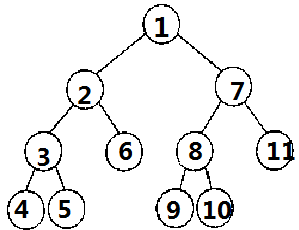
(圈里的都是结点的编号, 4、5、6、9、10、11号结点代表的分别是1、2、3、4、6、7)
(4、5、9、10你也可以任意作为6或11的儿子, 递归生成的是类似这样的, 这并不重要)
对于3 2 1 4 7(先不管需要更新的6)建完树见下图(建树过程同静态的,不明白的戳这里,上篇博客有讲)

(红色的是个数, 相同结点的个数省略了,同前一棵树)
对于C操作之前的Q,就跟静态的类似,减一减 找就好了
然后下面要更新了
对于更新, 我们不改变这些已经建好的树, 而是另建一批树S,用来记录更新,而这批线段树,我们用树状数组来维护
也就是树状数组的每个节点都是一颗线段树
一开始,S[0]、S[1]、S[2]、S[3]、S[4]、S[5](树状数组的每个节点)这些都与T[0]相同(也就是每个节点建了一棵空树)
对于C 2 6 这个操作, 我们只需要减去一个2,加上一个6即可
对于减去2
(树状数组i+lowbit(i)为i的父亲节点, 修改i,就要把i的所有父亲节点都修改了)
2在树状数组中出现的位置是 2、2+lowbit(2)=4 这两个位置,
因此要更新的是S[2]和S[4]这两个节点中的树
删去2后是这样
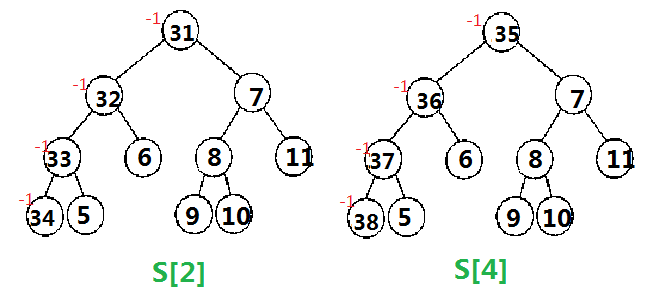
加上一个6 (同样是对于2号位置, 因此需要更新的仍是S[2]和S[4])
加上之后是这样
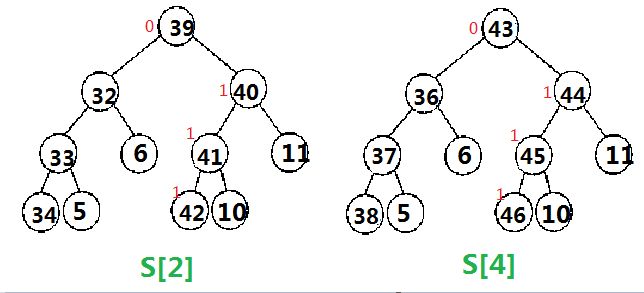
当查询的时候, 对树T的操作与静态的一致,另外再加上S树的值就好了

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 #define lson l, m 5 #define rson m+1, r 6 const int N=60005; 7 int a[N], Hash[N]; 8 int T[N], L[N<<5], R[N<<5], sum[N<<5]; 9 int S[N]; 10 int n, m, tot; 11 struct node 12 { 13 int l, r, k; 14 bool Q; 15 }op[10005]; 16 17 int build(int l, int r) 18 { 19 int rt=(++tot); 20 sum[rt]=0; 21 if(l!=r) 22 { 23 int m=(l+r)>>1; 24 L[rt]=build(lson); 25 R[rt]=build(rson); 26 } 27 return rt; 28 } 29 30 int update(int pre, int l, int r, int x, int val) 31 { 32 int rt=(++tot); 33 L[rt]=L[pre], R[rt]=R[pre], sum[rt]=sum[pre]+val; 34 if(l<r) 35 { 36 int m=(l+r)>>1; 37 if(x<=m) 38 L[rt]=update(L[pre], lson, x, val); 39 else 40 R[rt]=update(R[pre], rson, x, val); 41 } 42 return rt; 43 } 44 45 int lowbit(int x) 46 { 47 return x&(-x); 48 } 49 50 int use[N]; 51 void add(int x, int pos, int val) 52 { 53 while(x<=n) 54 { 55 S[x]=update(S[x], 1, m, pos, val); 56 x+=lowbit(x); 57 } 58 } 59 60 int Sum(int x) 61 { 62 int ret=0; 63 while(x>0) 64 { 65 ret+=sum[L[use[x]]]; 66 x-=lowbit(x); 67 } 68 return ret; 69 } 70 71 int query(int u, int v, int lr, int rr, int l, int r, int k) 72 { 73 if(l>=r) 74 return l; 75 int m=(l+r)>>1; 76 int tmp=Sum(v)-Sum(u)+sum[L[rr]]-sum[L[lr]]; 77 if(tmp>=k) 78 { 79 for(int i=u;i;i-=lowbit(i)) 80 use[i]=L[use[i]]; 81 for(int i=v;i;i-=lowbit(i)) 82 use[i]=L[use[i]]; 83 return query(u, v, L[lr], L[rr], lson, k); 84 } 85 else 86 { 87 for(int i=u;i;i-=lowbit(i)) 88 use[i]=R[use[i]]; 89 for(int i=v;i;i-=lowbit(i)) 90 use[i]=R[use[i]]; 91 return query(u, v, R[lr], R[rr], rson, k-tmp); 92 } 93 } 94 95 void modify(int x, int p, int d) 96 { 97 while(x<=n) 98 { 99 S[x]=update(S[x], 1, m, p, d); 100 x+=lowbit(x); 101 } 102 } 103 104 int main() 105 { 106 int t; 107 scanf("%d", &t); 108 while(t--) 109 { 110 int q; 111 scanf("%d%d", &n, &q); 112 tot=0; 113 m=0; 114 for(int i=1;i<=n;i++) 115 { 116 scanf("%d", &a[i]); 117 Hash[++m]=a[i]; 118 } 119 for(int i=0;i<q;i++) 120 { 121 char s[10]; 122 scanf("%s", s); 123 if(s[0]=='Q') 124 { 125 scanf("%d%d%d", &op[i].l, &op[i].r, &op[i].k); 126 op[i].Q=1; 127 } 128 else 129 { 130 scanf("%d%d", &op[i].l, &op[i].r); 131 op[i].Q=0; 132 Hash[++m]=op[i].r; 133 } 134 } 135 sort(Hash+1, Hash+1+m); 136 int mm=unique(Hash+1, Hash+1+m)-Hash-1; 137 m=mm; 138 T[0]=build(1, m); 139 for(int i=1;i<=n;i++) 140 T[i]=update(T[i-1], 1, m, lower_bound(Hash+1, Hash+1+m, a[i])-Hash, 1); 141 for(int i=1;i<=n;i++) 142 S[i]=T[0]; 143 for(int i=0;i<q;i++) 144 { 145 if(op[i].Q) 146 { 147 for(int j=op[i].l-1;j;j-=lowbit(j)) 148 use[j]=S[j]; 149 for(int j=op[i].r;j;j-=lowbit(j)) 150 use[j]=S[j]; 151 printf("%d\n", Hash[query(op[i].l-1, op[i].r, T[op[i].l-1], T[op[i].r], 1, m, op[i].k)]); 152 } 153 else 154 { 155 modify(op[i].l, lower_bound(Hash+1, Hash+1+m, a[op[i].l])-Hash, -1); 156 modify(op[i].l, lower_bound(Hash+1, Hash+1+m, op[i].r)-Hash, 1); 157 a[op[i].l]=op[i].r; 158 } 159 } 160 } 161 return 0; 162 }




