[主席树]HDOJ2665 && POJ2104 && POJ2761
主席树真是神奇的物种!
题意:给n、m
下面有n个数 (编号1到n)
有m个询问,询问的是上面的数的编号在[l,r]之间第k小的数
n、m的范围都是$10^5$
是主席树的入门题
借此来学习一下主席树
主席数利用函数式线段树来维护数列,一般用来解决区间第k大问题
空间时间的复杂度小于树套树(常数小)
划分树也可以解决区间第k大问题,但划分树不支持修改,主席树可以(用树状数组维护)
(这三道入门题都是无修改的)
我们先来YY一下这种求区间第k(大)小的题目···
最容易想到的做法就是对于每个询问,对[l, r]区间排个序,输出第k小
这样的复杂度是O($m\times nlogn$)


大家都很容易想到排序,但是对于每个询问每个区间排序的代价太大了...
再想想,让我们加入一些线段树的思想,
要求第k小,也就是与个数相关,那么我们可以 以[l,r]区间内的数的个数来建立一棵线段树
结点的值是数的个数,当我们要找第k小的数时,若左子树大于k,那么很显然第k小的数在左子树中;若左子树小于k,那么第k小的数在右子树中
建树的复杂度是O(nlogN),查询的复杂度是O(logN) (这里的N是不相同数的数量)
若我们仍对每个查询建树,那么复杂度丝毫没有降低(反而提高了),那有没有什么办法可以不要每次查询都建树呢?
(让我们联想一下前缀和) 假设我们知道[1, l-1]之间有多少个数比第k小的数小,那么我们只要减去这些数之后在[1, r]区间内第k小的数即是[l, r]区间内的第k小数
更确切的说,我们要求[l, r]区间内的第k小数 可以 用以[1, r]建立的线段树去减去以[1, l-1] 建立的线段树
这样能够减的条件是这两棵树必须是同构的。
若是不太明白, 我们来举个例子:
如有序列 1 2 5 1 3 2 2 5 1 2
我们要求 [5,10]第5小的数
(数列中不存在4、6、7、8 但根据原理就都写出来了,为方便理解,去掉了hash的步骤,实际的代码中其实只要一棵4个叶子节点的树即可)
(红色的为个数)
我们建立的[1, l-1] (也就是[1, 4])之间的树为
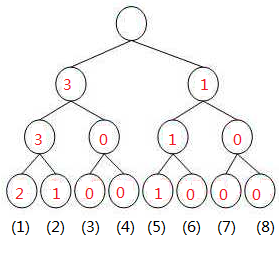
[1, r]也就是[1, 10]的树为
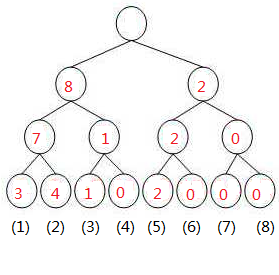
两树相减得到
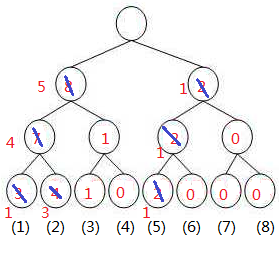
我们来找第5小的数:
发现左子树为5 所以第5小的数在左边, 再往下(左4右1) 发现左边小于5了 ,所以第5小的数在右边 所以第5小的数就是3了
同样的,我们只要建立[1, i] (i是1到n之间的所有值)的所有树,每当询问[l, r]的时候,只要用[1, r]的树减去[1, l-1]的树,再找第k小就好啦
我们将这n个树看成是建立在一个大的线段树里的,也就是这个线段树的每个节点都是一个线段树( ——这就是主席树)
最初所有的树都是空树,我们并不需要建立n个空树,只要建立一个空树,也就是不必每个节点都建立一个空树
插入元素时,我们不去修改任何的结点,而是返回一个新的树( ——这就是函数式线段树)
因为每个节点都不会被修改,所以可以不断的重复用,因此插入操作的复杂度为O(logn)
总的复杂度为O((n+m)lognlogN) (听说 主席树的芭比说 加上垃圾回收, 可以减少一个log~~~ 然而这只是听说)
你以为这样就结束了吗!!
你没有发现这样空间大到爆炸吗!!!
你在每个节点都建了一个线!段!树!这不MLE才有鬼呢!!!
那怎么办呢?
$T_i$表示一棵[1, i]区间的线段树
那么$T_i$与$T_{i-1}$的区别就只有当前插入的这个元素$a_i$以及它的父亲以及他父亲的父亲以及他父亲的父亲的父亲...
也就是改变的就只有他和他上面logn个数
所以,我们并不需要建一整棵树,我们只需要 单独建立logn个结点,跟$T_{i-1}$连起来就好了
这样树的空间复杂度(NlogN)
以下是代码:

1 #define lson l, m 2 #define rson m+1, r 3 const int N=1e5+5; 4 int L[N<<5], R[N<<5], sum[N<<5]; 5 int tot; 6 int a[N], T[N], Hash[N]; 7 int build(int l, int r) 8 { 9 int rt=(++tot); 10 sum[rt]=0; 11 if(l<r) 12 { 13 int m=(l+r)>>1; 14 L[rt]=build(lson); 15 R[rt]=build(rson); 16 } 17 return rt; 18 } 19 20 int update(int pre, int l, int r, int x) 21 { 22 int rt=(++tot); 23 L[rt]=L[pre], R[rt]=R[pre], sum[rt]=sum[pre]+1; 24 if(l<r) 25 { 26 int m=(l+r)>>1; 27 if(x<=m) 28 L[rt]=update(L[pre], lson, x); 29 else 30 R[rt]=update(R[pre], rson, x); 31 } 32 return rt; 33 } 34 35 int query(int u, int v, int l, int r, int k) 36 { 37 if(l>=r) 38 return l; 39 int m=(l+r)>>1; 40 int num=sum[L[v]]-sum[L[u]]; 41 if(num>=k) 42 return query(L[u], L[v], lson, k); 43 else 44 return query(R[u], R[v], rson, k-num); 45 } 46 47 int main() 48 { 49 // int t; 50 // scanf("%d", &t); 51 // while(t--) 52 // { 53 tot=0; 54 int n, m; 55 scanf("%d%d", &n, &m); 56 for(int i=1; i<=n; i++) 57 { 58 scanf("%d", &a[i]); 59 Hash[i]=a[i]; 60 } 61 sort(Hash+1, Hash+n+1); 62 int d=unique(Hash+1, Hash+n+1)-Hash-1; 63 T[0]=build(1, d); 64 for(int i=1; i<=n; i++) 65 { 66 int x=lower_bound(Hash+1, Hash+d+1, a[i])-Hash; 67 T[i]=update(T[i-1], 1, d, x); 68 } 69 while(m--) 70 { 71 int l, r, k; 72 scanf("%d%d%d", &l, &r, &k); 73 int x=query(T[l-1], T[r], 1, d, k); 74 printf("%d\n", Hash[x]); 75 } 76 // } 77 }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号