图论练习

主要是一些写的题的题解。

1. P10573 [JRKSJ R8] C0mp0nents

首先转化限制，\(|a_x-a_y|=k\) 的一个必要条件是 \(a_x\equiv a_y\pmod k\)。于是我们只关心模 \(k\) 同余的点之间的边。

先把这些点拿出来，然后就转化为了 \(k=1\) 的情形。不妨将点按编号大小从小到大排成一排。

考虑如何算 \(s=1\) 的答案，注意到答案的最终形态必定是 \([1,r]\) 的连通块，且 \(x\in[1,r)\) 必定向 \((x,r]\) 中的某个点连了边。

那么推广到一般情况，可以知道对于 \(s=i\) 的情况，答案的形态为 \([l,r]\) 的连通块。\(x\in[i,r)\) 必定向 \((x,r]\) 连了边。对称的情况是类似的。

为了得到上述 \(l,r\)，我们定义 \(L_i\) 表示只考虑 \(i\) 左侧的边，\(i\) 向左能连通 \([L_i,i]\) 的最远位置，\(R_i\) 同理。

容易发现 \(L_i=i\) 或 \(L_i=L_{i-1}\)。\(R_i\) 同理。于是扫一遍检查连边就可以得到 \(L_i\) 和 \(R_i\)。

于是答案的连通块必定包含于 \([L_{i-1},R_{i+1}]\) 中，将其分为三部分来看待以便得到答案：\([L_{i-1},i-1],[i,i],[i+1,R_{i+1}]\)。这里需要一点分类讨论：

1. 如果 \([i,i]\) 与左右都连通，即 \(L_i=L_{i-1} \land R_i=R_{i+1}\)，那么答案就是 \(R_{i+1}-L_{i-1}+1\)。

2. 如果 \([i,i]\) 与左右都不连通，那么答案就是 \(1\)。

3. 如果 \([i,i]\) 只与单侧连通，由于 \(L_i,R_i\) 的定义，并没有考虑到跨过 \(i\) 的边对连通性的影响。如果此时 \([L_{i-1},i-1]\) 与 \([i+1,R_{i+1}]\) 之间有边相连，那么答案应当同第一种情况（这时可以先将单侧变为 \(i\)，然后再将另一侧变为 \(i\)），否则只计算单边的答案。

现在的问题就是判定两个区间之间是否有边相连。

可以直接将边 \((u,v)\) 视为二维平面上一点，然后就是数矩形内是否有点。这样实现的复杂度是 \(O(m\log n)\)。

也可以发现 \(L_i,R_i\) 具有单调性。对于一条边 \((u,v)\) 考虑可以使得哪些 \(i\) 合法（\(u>v\)）。写出限制：\(v\ge L_{i-1}\land v\le i-1\land u\ge i+1\land u\le R_{i+1}\)。

发现符合条件的 \(i\) 是一段区间，进行差分可以标记出符合条件的 \(i\)。左右端点可以二分，复杂度 \(O(m\log n)\)。可以精细实现去掉二分，复杂度线性。

2. P9697 [GDCPC 2023] Canvas

由于后续操作可能覆盖前面的操作，这不好。时光倒流变成只有第一次操作有效。以下的顺序都是时光倒流之后的。

观察到赋值只会是 \(1\) 或 \(2\)，首先所有将两个位置都赋值为 \(2\) 的操作必定最先进行，将两个位置都赋值为 \(1\) 的操作必定最后进行。现在只用考虑将一个赋值为 \(1\)，另一个赋值为 \(2\) 的操作的顺序。

不妨记这样的一个操作为 \((u,v)\) 表示将 \(u\) 赋值为 \(1\) 并将 \(v\) 赋值为 \(2\)。容易发现一旦执行了 \((u,v)\) 后，所有 \((v,*)\) 的操作都可以按任意顺序执行了。

图论建模，将 \((u,v)\) 视作一条有向边，那么上面的过程描述的其实是从 \(u\) 出发的任意一条路径上，只有 \(u\) 可能被赋值为 \(1\)，其他的点必然被赋值为 \(2\)。称这里的 \(u\) 为起始点。

对图进行强连通分量缩点，显然只有入度为 \(0\) 的强连通分量中才可能出现被赋值为 \(1\) 的点。入度非 \(0\) 的强连通分量中的每个点，必然有从入度为 \(0\) 的强连通分量中的点到它的路径，所以一定会被赋值为 \(2\)。

对于入度为 \(0\) 的强连通分量，优先选择已经被将两个点都赋值为 \(2\) 的操作赋值过的点作为起始点。否则任意选一个点作为起始点均可。

简单 DFS 即可求得操作顺序。由于时光倒流，最后记得翻转一下。

时间复杂度 \(O(n+m)\)。

3. CF1967D Long Way to be Non-decreasing

由于一次操作是对于一个下标集合，即对多个数同时操作，那么设位置 \(i\) 要被操作 \(c_i\) 次，答案应当为 \(\max\limits_i c_i\)。

要最小化这个式子，套路地想到二分一个数的最大操作次数。

观察这个操作，如果将 \(x\) 向 \(b_x\) 连边，就会得到内向基环树森林。于是从一个数变化到另一个数的操作次数就是两点在内向基环树上的距离。

这里需要处理一下基环树。分类讨论一下祖先后代关系和环上的情况即可 \(O(1)\) 求距离，注意判断不可达的情况。

在二分判定中，贪心地将当前的数变成在操作次数限制之内最小的可达的数。可以在值域上用指针扫来实现。由于指针单调不降，一次判定是 \(O(m)\) 的。

于是复杂度是 \(O(m\log m)\)。

4. CF1956F Nene and the Passing Game

先不妨 \(i>j\)，那么条件可以转化为 \(i-j\ge l_i+l_j\land i-j\le r_i+r_j\)。

再化一下，\(i-l_i\ge j+l_j\) 且 \(i-r_i\le j+r_j\)。这显然二维偏序，满足这个二维偏序的 \(i\) 和 \(j\) 相互可达，最终的答案就是连通块个数。

处理二维偏序，直接扫描线。统一一下不等号方向，得到 \(i-l_i\ge j+l_j\land r_i-i\ge -j-r_j\)。不妨将此处的 \(i\) 视作一次合并操作，也即扫到这样的 \(i\) 处就尝试合并一些连通块。将一个位置 \(x\) 拆成上述的 \(i\) 和 \(j\) 两个元素，记录类型和两个对应的值。对于 \(i-l_i\ge j+l_j\)，直接排序满足这一条限制，注意合并操作应当在值相等时更靠后。利用 set 维护 \(r_i-i\ge -j-r_j\) 这一限制，每次合并相当于从 set 中取出一段前缀进行合并，合并后将新的连通块中的最小权值连带标号重新插入到 set 中即可。

最后统计答案就直接数连通块个数。

5. P9150 邮箱题

由于 \(k_i\) 构成排列，所以到一个点之后要去的下一个点是确定的。套路地拆置换环，从一个点出发，能到的点必然是置换环上的一段。

先把一个环拿出来，考虑断环成链。一个点的答案就是链上靠前的位置处的答案。

考虑怎么暴力。从 \(i\) 出发时，维护最长的可以到达的一段链（称之可达链），每次尝试拓展到下一个位置。如果可以拓展，那么下一个位置必然和可达链上的一个位置之间有边，且这个位置与可达链最后一个位置强连通。

直接用两个并查集维护链和强连通分量就是暴力了，复杂度是 \(O(n^2\alpha(n))\)。

考虑优化这个过程。我们自然想到能否让一个点的答案从上一个位置转移过来。由于一个点的可达链向后拓展，我们在链上从后往前加点。加入一个点后，我们要尝试合并若干条可达链以及若干个强连通分量。

合并两条链的过程需要考虑这两条链之间是否有边。记 \(pre_i\) 表示链上位置 \(i\) 的在它之前距离它最近且有指向它的边的位置。设第一条链的开头为 \(u\)，末尾为 \(x\)，第二条链的开头为 \(x+1\)，那么只需检查是否满足 \(u\le pre_{x+1}\le x\)，若满足，即可合并。

链合并之后强连通分量该怎么办？两个强连通分量要想合并，其必然在同一条可达链上，且后一个强连通分量向前一个强连通分量有边。注意到两条链如果合并，那么新加入的点一定产生了贡献，否则不会合并或者会提前合并。所以必然是新加入的点使得第一条链末尾的强连通分量拓展了，于是第一条链整体必然是一个强连通分量。如果不是，就无法进行合并链的操作。

于是对于一条链，维护编号最大的具有向前连的边的强连通分量的编号。由于前面整体必然是一个强连通分量，所以不必知道连到哪个位置，直接从第一个强连通分量一直合并到这个强连通分量即可。合并到这里后要清空维护的编号。

实现中维护的链的编号和强连通分量的编号其实就是右端点。于是可以 \(O(1)\) 计算答案。第一问就是可达链的长度，第二问就是所在强连通分量的长度。总复杂度 \(O(n\alpha(n))\)。

6. CF241E Flights

分析一下，从 \(1\) 出发到 \(n\) 的每一条路径的长度相同，是可以推出从 \(1\) 出发到可能的路径上的点 \(i\) 的每一条路径的长度相同的，容易反证。

于是先扔掉从 \(1\) 出发到 \(n\) 不可能经过的点。然后设从 \(1\) 出发到 \(i\) 的相同的距离为 \(dis_i\)。对于一条有向边 \((u,v)\)，由题可知 \(1\le dis_v-dis_u\le 2\)。于是差分约束即可。

7. P10665 [AMPPZ2013] Bytehattan

强制在线删边，不能离线和时光倒流改删边为加边。但是这是平面图，原图上删边意味着两个平面合并，在对偶图上是加边，于是转对偶图。

删掉一条边后如何判这条边的两端是否连通？不连通时，必然有一圈平面将一个端点围起来，所以对偶图上成环时就不连通。用并查集维护即可。

8. CF429E Points and Segments

首先假设端点没有重合的，那么区间的被覆盖次数一定是奇偶交替的。被覆盖偶数次的区间，蓝色与红色出现次数要保证相等。于是考虑其相邻的两个被覆盖奇数次的区间。

对于一个区间，它的左右端点必然是两条线段的的端点。可以手玩发现，如果左右端点都是线段的左端点或者右端点，那么这两条线段应当异色。否则应当同色。

这样就可以 2-SAT。上述过程在端点有重合时也是正确的，因为只是在一个点上不断 \(+1\) 和 \(-1\)。最后必然绝对值不超过 \(1\)。

并且可以证明这样必然是有解的。

瓶颈在于排序。\(O(n\log n)\)。

9. [ARC165F] Make Adjacent

首先分析步数最小。记 \(l_x,r_x\) 为 \(x\) 两次出现的位置。\(x\) 和 \(y\) 在原序列中只会有三种位置关系：\(xxyy\)，\(xyxy\)，\(xyyx\)。发现第三种情况怎么操作都不影响最小步数，前两种情况要求 \(x\) 最后必在 \(y\) 之前。

于是形式化，当且仅当 \(l_x<l_y\land r_x<r_y\) 时 \(x\) 必须在 \(y\) 之前。这个偏序关系可以建图，然后跑最小字典序的拓扑序即可。

现在就剩优化建图。发现这是二维偏序，可以主席树搞一搞。也可以 CDQ 分治。具体地，先按一维排序，在归并的过程中对另一维排序，最后在一段区间中就是一个点向一段后缀连边，后缀优化建图即可。

最后跑拓扑排序时，用队列存新建的虚点，用优先队列存原来的点。如果还有虚点就优先从虚点拓展，没有虚点时再选最小的原来的点。这样就保证字典序最小。

\(O(n\log n)\)。

10. [ARC153F] Tri-Colored Paths

发现限制过于宽松和抽象，选择单步容斥主动加强限制。现在就是求染了三种颜色的前提下没有三色路径的方案数。

所有染了三种颜色的方案数是好求的，简单容斥得到 \(3^m-3\cdot 2^m+3\)。

考虑树上的情况，发现若钦定一个点为根，那么这个点的一棵子树中的边必然同色。发现这样的贡献还是和上面类似的形式，不妨设 \(f(x)=3^x-3\cdot 2^x+3\)，那么一个点的贡献就是 \(f(deg_u)\)，整棵树的答案就是 \(\sum f(deg_u)\)。容易发现这样不会算重。

拓展到一般的图上，首先考虑环。

对于一个有三种颜色的环，如果其长度 \(\ge 4\)，那么容易构造出一条在这个环上的三色简单路径。所以三色环只可能是三元环。

考虑这个三元环外部的边，如果这个三元环只有一个点向外连了边，那么这些边只能和这个点在环上的对边同色。否则容易构造三色路径。这里有 \(6\) 种方案。

如果有两个点向外连边，且连向了两个不同的点。首先这两条边必然和对边同色，但是这样就又出现了三色路径：两条向外连的边和夹边。于是不行。

如果有 \(2\) 个或 \(3\) 个点向外同一个点连边。容易检验 \(3\) 个点的情况不行，\(2\) 个点的情况可以，但是限制了不能再向外连边。于是这种情况需要在一开始特判。

对于一个有两种颜色的环，考虑环外的第三种颜色的边，由于连通，必然可以走到环上，所以肯定有三色路径。故不能出现双色环。

所以一个环上的边只能是一种颜色。或者是三元环的特殊情况。这里建圆方树，将一个点双视作一个大环。然后就是树上情况了。最终答案的形态必然是对于一个圆点，其一个子树中染相同颜色。且由于三色的限制，度数一定要 \(\ge 3\)。

最后的方案数就是树上的答案加上三元环的特判。再容斥回去即可。

11. [AGC035E] Develop

一种方案对应着唯一一种删去的数的集合，考虑对这个计数。将 \(x\) 向 \(x-2\) 和 \(x+k\) 连边，那么一个集合中的数能被删去，当且仅当不构成环。

对 \(k\) 分奇偶讨论。如果 \(k\) 为偶数，那么奇数偶数是分开的，可以分开做再乘起来。观察奇数/偶数形成的一条链，发现不形成环的限制等价于不连续选 \(\dfrac{k}{2}\) 个点。简单 DP 即可。

如果 \(k\) 是奇数，那么奇偶之间会有边。借题解区一张图，

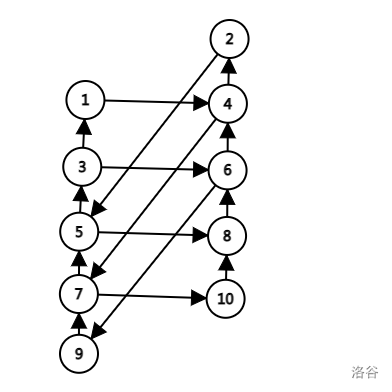
可以发现其中的环长都为 \(k+2\)，一个环的形态为从左边开始向上走若干步，然后向右走一步，最后向左下走回去。不妨钦定只在环的左下角计算这个环。

还发现奇数链和偶数链错开了一部分，其他部分自然分层。不妨对一层设状态。设 \(f_{i,l}\) 表示考虑了前 \(i\) 层，从第 \(i\) 层左下角开始选的最长链长度为 \(l\)。这里保证 \(l\le k+1\) 即可保证无环。

但是你发现这个状态并不好转移，因为完全不知道右侧选了什么，该怎么选。于是增加一维辅助转移。设 \(f_{i,l,r}\) 表示考虑了前 \(i\) 层，从第 \(i\) 层左下角开始选的最长链的长度为 \(l\)，从第 \(i\) 层右下角开始在右侧选的最长的一段长度为 \(r\)。

这里注意 \(l\) 可以从左侧延伸到右侧，而 \(r\) 只会在右侧选。

可以讨论转移了。一层的转移无非两侧的点都选，一侧的点选，两侧的点都不选。讨论一下：

1. 都选：注意层数 \(i\) 的范围，要保证左右都有点才能转移。此时最长链可能是原本的最长链延伸而来，也可能是新得到一条最长链：从这一层左侧的点开始到 \(r\)。于是转移即 \(f_{i,\max\left(l+1,r+2\right),r+1}\gets f_{i-1,l,r}\)。

2. 都不选：那么直接清空左右的连续段。\(f_{i,0,0}\gets f_{i-1,l,r}\)。

3. 只选右边：清空左边的连续段。\(f_{i,0,r+1}\gets f_{i-1,l,r}\)。

4. 只选左边：清空右边的连续段，但是左侧的情况还要讨论。如果本来的左侧连续段长度不为 \(0\)，那么 \(f_{i,l+1,0}\gets f_{i-1,l,r}\)。如果本来左侧连续段长度为 \(0\)，那么现在只选左边，之后是不可能成环的，因为没有延伸到右边。所以转移是 \(f_{i,0,0}\gets f_{i-1,0,r}\)。

这样就做完了。\(O(n^3)\)。

12. CF843D Dynamic Shortest Path

首先跑一遍最短路，可以得到 \(dis_v\le dis_u+w\)。然后将 \(c\) 条边的边权 \(+1\)，可知最短路增量不超过 \(c\)。写出带增量的式子， \(dis_v+\Delta_v\le dis_u+\Delta_u+w\)。于是 \(\Delta_v\le \Delta_u+dis_u-dis_v+w\)。这是类似最短路的形式，对增量跑最短路即可。

最短路有基于值域的 \(O(V+n+m)\) 的做法。一般的最短路用优先队列来从小到大转，这里可以对每个值开队列，手动在值域上从小到大转。这样就可以做到一次询问是 \(O(c+n+m)\)。总的复杂度是可以接受的。

13. CF589H Tourist Guide

对每个连通块分开考虑。可以发现在树上的情形，一棵树上至多有一个关键点无法匹配。如果两条路径有交，显然可以调整到无交。于是对一个连通块跑任意一棵生成树，然后在树上搞匹配。

具体地，在一个子树内，贪心地进行匹配即可。

14. [ARC144E] GCD of Path Weights

先拆点，点权搞到边上。

经典结论，若答案为 \(x\)，则存在一种分配权值 \(d_u\) 的方案，使得对于有向边 \((u,v,w)\)， \(d_u+w\equiv d_v\pmod x\)。

于是带权并查集维护 \(w_u\)，表示 \(d_u+w_u\equiv d_{rt}\pmod x\)。如果遇到环，则对 \(x\) 有双重限制，将答案与 \(d_u+w-d_v\) 取 \(\gcd\) 即可。容易发现边权为 \(-1\) 的边不会有限制，直接不管。