Log Concave Sequences Gym - 102302H - 矩阵快速幂

长度为\(n\)，且只有{0,1,2}，并且满足\(a_{i - 1}*a_{i + 2} ≤ a_{i}^2, i \in[2, n - 1]\)

首先进行打表发现
三个序列里

0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
0 2 0
0 2 1
0 2 2
1 0 0
1 1 0
1 1 1
1 2 0
1 2 1
1 2 2
2 0 0
2 1 0
2 2 0
2 2 1
2 2 2

都是条件的，然后再后面加{0,1,2}，那么就对于某一个序列，就是由前面的序列进行相加过来的

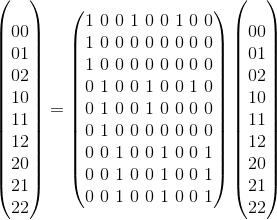
那么也就是说可以设一个辅助矩阵进行优化即可

#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long  long
using namespace std;
const int mod = 1e9 + 7;
ll m[9][9] ={
    {1,0,0,1,0,0,1,0,0},
    {1,0,0,0,0,0,0,0,0},
    {1,0,0,0,0,0,0,0,0},
    {0,1,0,0,1,0,0,1,0},
    {0,1,0,0,1,0,0,0,0},
    {0,1,0,0,0,0,0,0,0},
    {0,0,1,0,0,1,0,0,1},
    {0,0,1,0,0,1,0,0,1},
    {0,0,1,0,0,1,0,0,1}
};
struct Matrix{//矩阵
    int n,m;
    ll a[9][9];
    Matrix(int x,int y):n(x),m(y){memset(a,0,sizeof(a));}
    Matrix operator * (const Matrix &b){
        Matrix ans(n,b.m);
        for(int i = 0; i < n; i++){
            for(int j = 0; j < b.m; j++){
                for(int k = 0; k < m; k++){
                    ans.a[i][j] = (ans.a[i][j] + a[i][k] * b.a[k][j] % mod) % mod;
                }
            }
        }
        return ans;
    }
};
Matrix ksm(Matrix a, ll b){//矩阵快速幂
    Matrix ans(a.n,a.m);
    int maxx = max(a.n, a.m);
    for(int i = 0; i < maxx; i++)ans.a[i][i] = 1;
    while(b){
        if(b & 1)ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}
ll Fib(ll n){
    Matrix base(9, 9);
    for(int i = 0; i < 9; i++)
        for(int j = 0; j < 9;j++)
            base.a[i][j] = m[i][j];
    Matrix ans = ksm(base, n - 2);
    ll sum = 0;
    for(int i = 0 ; i < 9;i++)
        for(int j = 0; j < 9;j++)
            sum =( sum + ans.a[i][j] ) % mod;
    return sum;
}
int main(){
    ll n;
    scanf("%lld", &n);
    printf("%lld\n", Fib(n));
    return 0;
}