P4429 [BJOI2018] 染色

Link：P4429 [BJOI2018] 染色。

显然，每个联通块独立，那么我们考虑一个联通块的情况。

二分图

首先，图一定是二分图。

如果不是二分图，那么我们给所有点都给予同一个集合，这样它就无法染色，就寄了。

偶环

我们考虑一个四元环，如果按下面的方式分配集合：

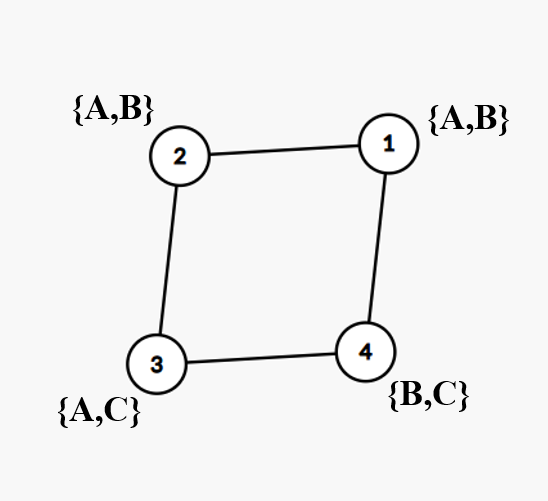
那么无论怎么染色，点 \(1\) 和点 \(2\) 的颜色都是确定的。

这个构造可以推广到更大的环上。也就是说，对于一个偶环，如果我们选取任意两个相邻点，给它们分别赋成 \(\{A,C\}\) 和 \(\{B,C\}\)，其他的都赋成 \(\{A, B\}\)，那么这些赋成 \(\{A,B\}\) 点的颜色就确定了。还有一个性质，如果我们把上图中点 \(3\) 和点 \(4\) 赋值的颜色集合反过来，即点 \(3\) 赋为 \(\{B,C\}\)，点 \(4\) 赋为 \(\{A,C\}\)，你会发现点 \(1\) 和点 \(2\) 的颜色也会有变化。

对于两个有交的环，如下图：

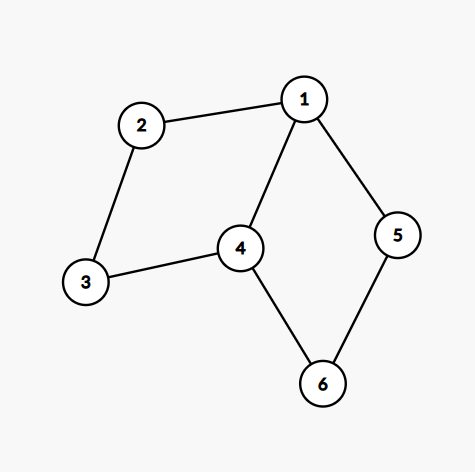
显然，这样一定会寄。因为我们可以自由给点 \(2\) 点 \(3\) 和点 \(5\) 点 \(6\) 赋值。如果它们赋相反的，那么点 \(1\) 和点 \(4\) 就矛盾了。这样，我们得到了一个重要性质：两个环有交且对于每个环，去掉交点后点数仍大于等于 \(2\)，就会寄掉。

其实，不一定要有交，在一个联通块也行，如下图：

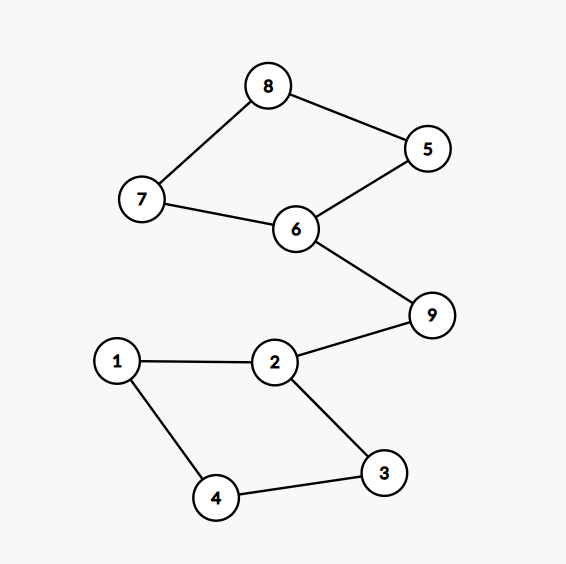
在这里，我们可以操纵点 \(2\) 和点 \(6\) 的颜色。比如让点 \(2\) 必为 \(A\)，点 \(6\) 必为 \(B\)。此时给点 \(9\) 的集合赋为 \(\{A,B\}\)，就寄了。

我们将上面的性质推广到了一个联通块内的环，这样就会好做很多。

一度点

这些一度点显然是没有用的，我们之间按拓扑排序的方式删掉就行。

三度点

这里，我们只讨论点的度数最大为 \(3\) 的情况。也就是说图上只有二度点或三度点。

两个三度点

首先，如果只有一条边连接它们，如下图：

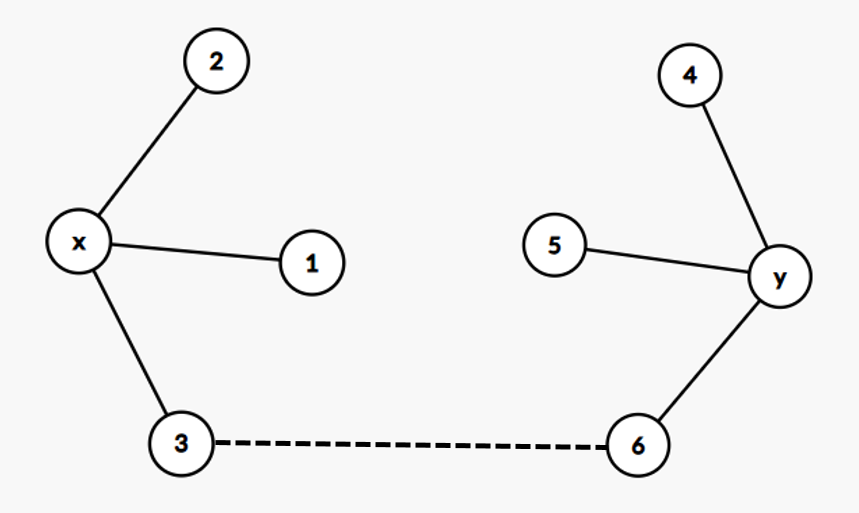
此时，由于除了点 \(x\) 和点 \(y\) 其他所有点都是二度点，所以必定是点 \(1\) 绕一个环回到点 \(2\)，点 \(4\) 绕一个环回到点 \(5\)。但这样一定有两个环了，还在一个联通块内，并且去掉交点后点数显然大于等于 \(2\)，就寄掉了。

如果恰好有两条边连接它们，如下图：

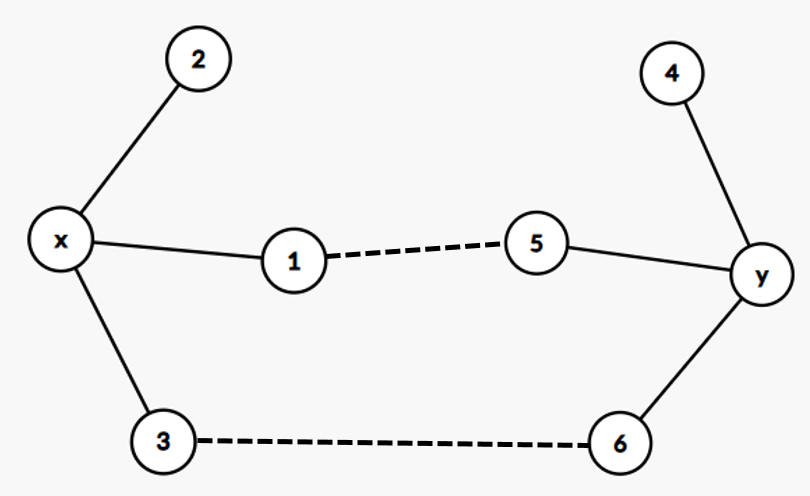
显然，从点 \(4\) 出发的路径不能经过虚线上的点，否则会产生三度点。也不能到达点 \(2\)，因为这样就会有三条边。所以，它只能绕回去。可是，这样一定会产生一个三度点，甚至产生一个四度点（绕回到点 \(y\)）。所以，这种情况是不可能出现的。

如果如果恰好有三条边连接它们，如下图：

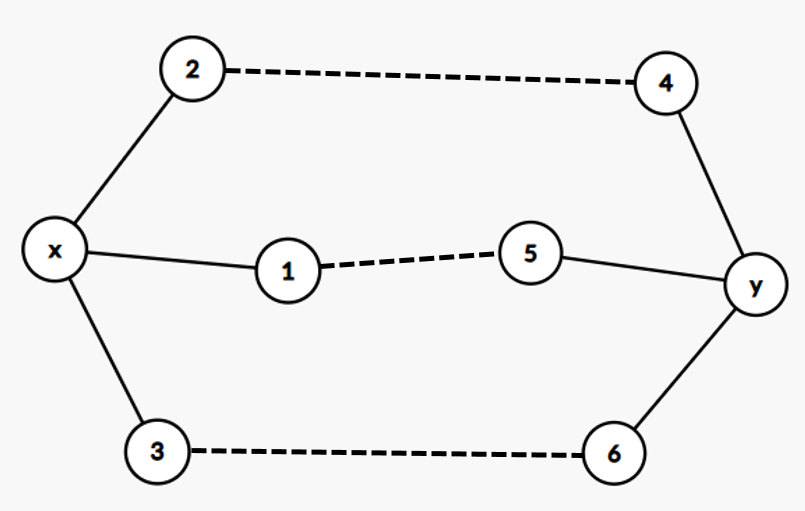
它里面有 \(3\) 个环，对于任意两个环，它们除去交点的部分都是一条从点 \(x\) 到点 \(y\) 的路径（不包括端点）。这样，我们只需要让路径只有一个点或者没有点即可。只有一条这样的路径显然是不行的，如下图：

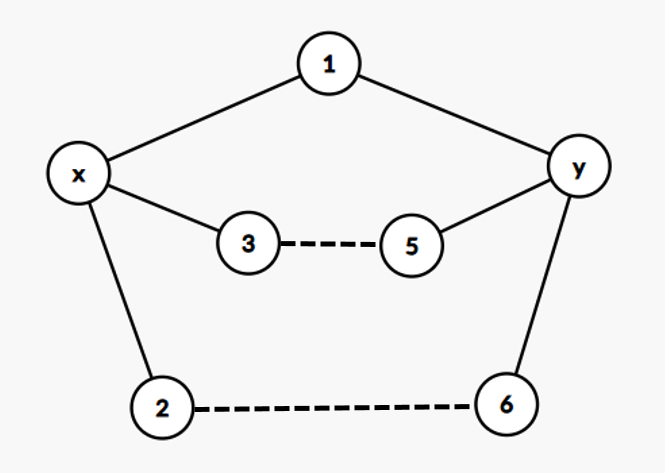
考虑环 \((x,1,y,5,3)\) 和环 \((x, 1, y, 6, 2)\)，去掉公共部分后剩下 \((5,3)\) 和 \((6,2)\)，显然都有至少两个点，就寄了。所以说，我们必须要两个只有一个点或者没有点的路径，如下图：

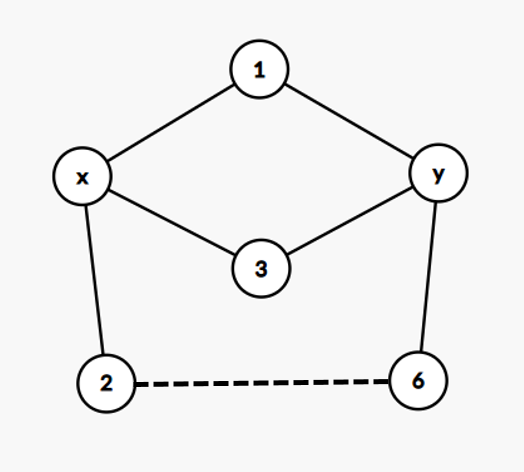
这样就是可行的，无论怎么构造都卡不掉。

综上，我们可以总结两个三度点时的规律：对于三度点 \(x\) 和三度点 \(y\)，如果存在三条不同的从点 \(x\) 到点 \(y\) 的路径，且这三条路径中点数（不包含端点）小于等于 \(1\) 的路径有至少两条，则这个图合法。否则就寄了。

三个以上三度点

任意拎出来两个三度点，如果在上面的分析中它们不合法显然就寄了，考虑一种在上面的分析中合法的情况，也就是上面那个图。

首先，点 \(1\)、点 \(3\) 和路径 \((2, 6)\) 中必有一个三度点。如果点 \(1\) 或点 \(3\) 是三度点，一种情况是它连接路径 \((2, 6)\)，如下图：

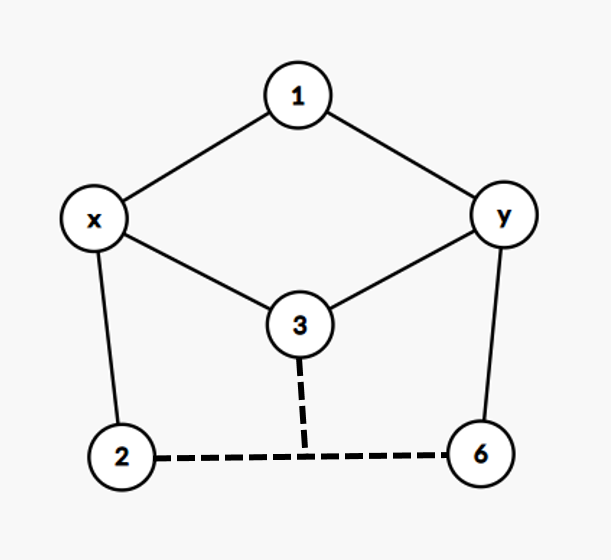
显然寄了，因为最底下的两个环去掉交点的部分显然多于两个点。另一种情况是它单独挂着一个环，如下图：

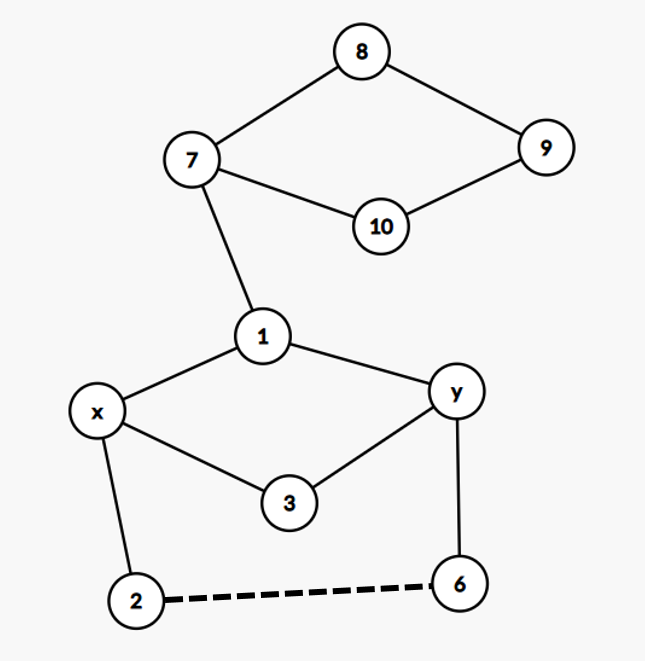
这也寄了，考虑环 \((7,8,9,10)\) 和环 \((x,1,y,6,2)\)，它们寄的很明显。所以说，点 \(1\) 和点 \(3\) 均为二度点。其实三度在路径 \((2, 6)\) 中的情况也是差不多的，它只能绕回路径 \((2, 6)\) 或者挂着一个环，这两种显然都会寄，我就不画图了。

综上，如果图中有三个以上三度点，那么一定寄。

四度以上点

观察这个四度以上点，如下图：

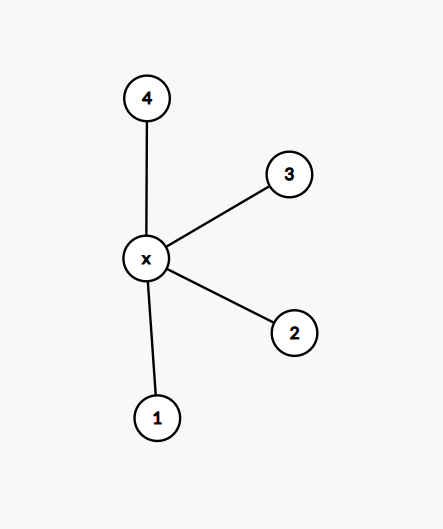
对于任何一个相邻点，它都有两种情况，一种是挂着一个环，另一种是绕回另一个相邻点。显然，有挂环的情况是会寄的，但如果没有挂环，那它们之间任意两个点都会形成一个环，我们选取环 \((1,x,2)\) 和环 \((3,x,4)\) 就寄了。如果不明白大家可以手玩一下。

综上，如果图中有四度以上点，那么一定寄。

做法

二分图染色判断即可。判断路径长度只需要枚举中间那个点即可。时间复杂度线性。挺好写的，跑的也挺快。代码。