题解：P9576 「TAOI-2」Ciallo～(∠・ω< )⌒★

Luogu 专栏：Link。

如果在分割前 \(t\) 就在 \(s\) 里面，并且分割时 \(t\) 没有被“割开”，也就是 \([l, r]\) 与 \([l ^ \prime, r ^ \prime]\) 不交（这里将 \(l^\prime\) 和 \(r^\prime\) 对应到了原来的 \(s\) 串中），可以直接统计。

接下来我们讨论 \(t\) 被割开，也就是 \(t\) 由 \([l ^ \prime, l]\) 与 \([r, r ^ \prime]\)（这里区间表示 \(s\) 的子串）组成时的情况。

首先有一种非常暴力的做法，枚举字符串 \(t\) 的分割点，然后在 \(s\) 中匹配。

举个例子，就针对题目中第一个样例，我们如果将 \(t\) 分割成：

\[{\color{red}\texttt{a}}{\color{blue}\texttt{ba}} \]

那么它在 \(s\) 中的一组匹配是：

\[\texttt{a}{\color{red}\texttt{a}}\texttt{bbaa}{\color{blue}\texttt{ba}} \]

其实这就相当于在 \(s\) 中删去了中间的 \(\texttt{bbaa}\)，剩下的串拼成了 \(\texttt{a}{\color{red}\texttt{a}}{\color{blue}\texttt{ba}}\)，最后再选取出了 \({\color{red}\texttt{a}}{\color{blue}\texttt{ba}}\)。

这样做总复杂度是 \(O(n^3)\)，实现好的话也许可以 \(O(n^2)\)，但这两种复杂度都是不能接受的。

观察上述做法，发现它依赖于分割点，这样复杂度一定有一个枚举分割点的 \(O(n)\)，很难优化。

不妨换个角度入手，观察上面的例子，你会发现红色部分（就是 \(\color{red}\texttt{a}\)）是 \(t\) 的一段前缀，蓝色部分（就是 \(\color{blue}\texttt{ba}\)）是 \(t\) 的一段后缀。再观察它们在 \(s\) 中出现的位置，\(\color{red}\texttt{a}\) 是 \(s\) 的后缀 \({\color{red}\texttt{a}}\texttt{bbaa}{\color{blue}\texttt{ba}}\) 的一段前缀，\(\color{blue}\texttt{ba}\) 是 \(s\) 的前缀 \(\texttt{a}{\color{red}\texttt{a}}\texttt{bbaa}{\color{blue}\texttt{ba}}\) 的一段后缀。

仔细观察上面的例子与它的性质，将它刻画成更一般的形式。这样，你会发现，合法的情况都形如下图：

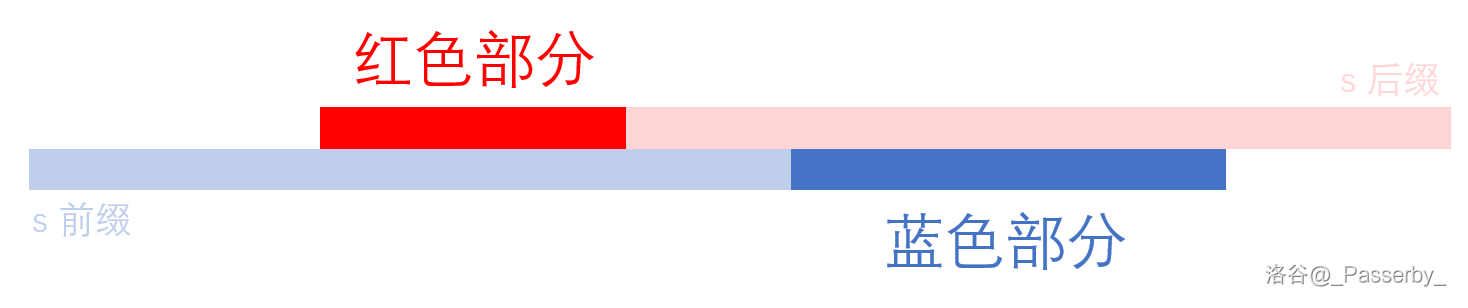
这里有两个性质，等会会用到：

1. \(s\) 的前后缀不能离得太近，要不然中间没有可以切开的地方。具体地，它们（端点）的距离要大于 \(\lvert t \rvert\)。
2. 红色部分的长度与蓝色部分的长度之和等于 \(\lvert t \rvert\)。

还是上面那个图，现在，我们固定这个前缀和后缀。记 \(\text{lcp}\) 表示这个后缀与 \(t\) 的最长公共前缀，记 \(\text{lcs}\) 表示这个前缀与 \(t\) 的最长公共后缀，在图中可以画成：

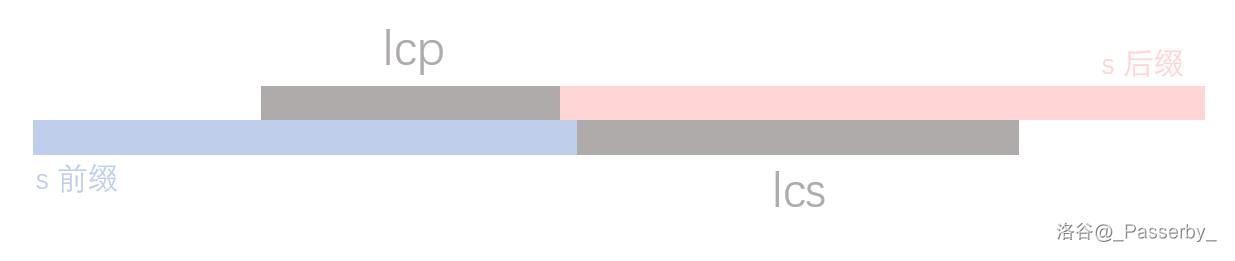
你会发现，红色部分不超过 \(\text{lcp}\)，蓝色部分不超过 \(\text{lcs}\)，即：

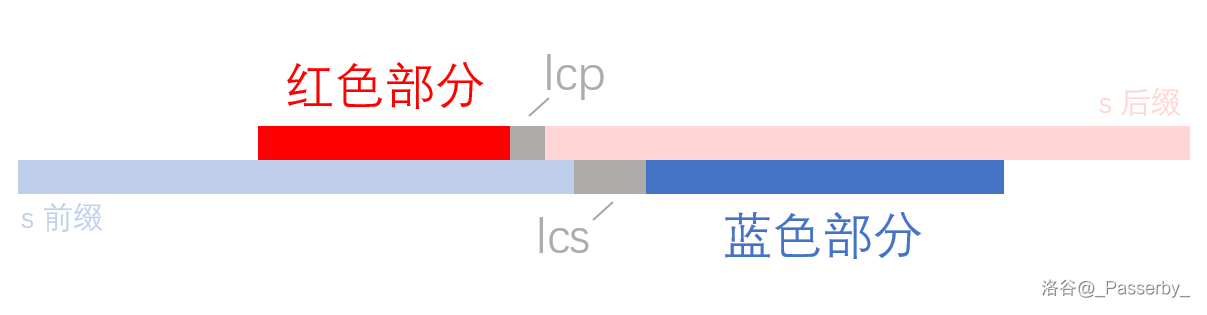
也就是说，一个 \(\text{lcp}\) 贡献了长度为 \(1\sim \lvert \text{lcp} \rvert\) 的前缀，一个 \(\text{lcs}\) 贡献了长度为 \(1\sim \lvert \text{lcs} \rvert\) 的一个后缀。这样，我们就可以枚举 \(s\) 的前缀和后缀，然后根据性质二直接统计答案。这样做时间复杂度是 \(O(n^2)\)，不能接受。

考虑优化。根据性质一，我们可以双指针枚举前缀和后缀。观察一个 \(\text{lcs}\)，根据性质二，它需要的前缀长度为 \(\lvert t \rvert - \lvert \text{lcs} \rvert\) 到 \(\lvert t \rvert - 1\)。这样，我们每次枚举到一个前缀，就在它可贡献范围内（\(1\sim \lvert \text{lcp} \rvert\)）区间加一，枚举到一个后缀时，就统计它需要的前缀长度（\(\lvert t \rvert - \lvert \text{lcs} \rvert\) 到 \(\lvert t \rvert - 1\)）的区间和，线段树维护即可，时间复杂度 \(O(n \log n)\)。

求 \(\text{lcp}\) 和 \(\text{lcs}\) 可以使用扩展 KMP 算法（Z 函数）在 \(O(n)\) 的时间复杂度内求出，总时间复杂度 \(O(n \log n)\)。

当然，你也可以把上面的限制刻画成一个二元偏序关系，然后直接二维数点解决。

代码：

#include <bits/stdc++.h>
#define int long long 
#define ls u << 1
#define rs u << 1 | 1
using namespace std;

const int N = 1e6 + 10;
typedef long long ll;
int n, m;
char a[N], b[N];
int f[N], p[N], s[N];
int ans = 0;

struct tree{
    int l, r;
    int val, lzy;
}t[N << 2];

void pushup(int u) {
    t[u].val = t[ls].val + t[rs].val;
}
void maketag(int u, int x) {
    t[u].val += (t[u].r - t[u].l + 1) * x;
    t[u].lzy += x;
}
void pushdown(int u) {
    if (!t[u].lzy) return ;
    maketag(ls, t[u].lzy);
    maketag(rs, t[u].lzy);
    t[u].lzy = 0;
}
void build(int u, int l, int r) {
    t[u].l = l, t[u].r = r;
    if (l == r) return ;
    int M = (l + r) >> 1;
    build(ls, l, M);
    build(rs, M + 1, r);
    pushup(u);
}
void modify(int u, int l, int r, int x) {
    if (l <= t[u].l && t[u].r <= r) maketag(u, x);
    else {
        int M = (t[u].l + t[u].r) >> 1;
        pushdown(u);
        if (l <= M) modify(ls, l, r, x);
        if (r > M) modify(rs, l, r, x);
        pushup(u);
    }
}
int query(int u, int l, int r) {
    if (l <= t[u].l && t[u].r <= r) return t[u].val;
    int M = (t[u].l + t[u].r) >> 1, res = 0;
    pushdown(u);
    if (l <= M) res += query(ls, l, r);
    if (r > M) res += query(rs, l, r);
    pushup(u);
    return res;
}


signed main() {
    cin >> a + 1 >> b + 1;
    n = strlen(a + 1), m = strlen(b + 1);
    b[m + 1] = '*';
    for (int i = m + 2; i <= m + n + 1; i++) b[i] = a[i - m - 1];
    int k1 = 0, k2 = 0;
    f[1] = m;
    for (int i = 2; i <= m + n + 1; i++) {
        if (k2 >= i) f[i] = min(k2 - i + 1, f[i - k1 + 1]);
        while (i + f[i] <= n + m + 1 && b[1 + f[i]] == b[i + f[i]]) f[i]++;
        if (i + f[i] - 1 >= k2) k1 = i, k2 = i + f[i] - 1;
    }
    for (int i = m + 2; i <= m + n + 1; i++) p[i - m - 1] = f[i];
    reverse(a + 1, a + n + 1);
    reverse(b + 1, b + m + 1);
    for (int i = m + 2; i <= m + n + 1; i++) b[i] = a[i - m - 1];
    memset(f, 0, sizeof f);
    k1 = 0, k2 = 0;
    f[1] = m;
    for (int i = 2; i <= m + n + 1; i++) {
        if (k2 >= i) f[i] = min(k2 - i + 1, f[i - k1 + 1]);
        while (i + f[i] <= n + m + 1 && b[1 + f[i]] == b[i + f[i]]) f[i]++;
        if (i + f[i] - 1 >= k2) k1 = i, k2 = i + f[i] - 1;
    }
    for (int i = m + 2; i <= m + n + 1; i++) s[i - m - 1] = f[i];
    reverse(s + 1, s + n + 1);
    build(1, 1, n);
    for (int i = 1; i <= n; i++) {
        int j = m + i;
        if (j > n) break;
        if (p[i]) modify(1, 1, p[i], 1);
        if (s[j]) ans += query(1, max(1ll, m - s[j]), m - 1);
    }
    for (int i = 1; i <= n; i++) {
        if (p[i] < m) continue;
        int l = i - 1, r = i + p[i];
        if (l >= 1) ans += l * (l + 1) / 2;
        if (r <= n) ans += (n - r + 2) * (n - r + 1) / 2;
    }
    cout << ans << "\n";
    return 0;
}