分层图 + 最短路
分层图 + 最短路
定义:
分层图就是普通图变为立体的
适用范围:
一些图论题,比如最短路、网络流等,题目对边的权值提供可选的操作,比如可以将一定数量的边权减半或变为零,在此基础上求解最优解。
算法:
Dijkstra 或 SPFA (Floyed 没写过)
例题1
洛谷P4822 BJWC2012冻结
题意:
可以将 k条双向边的边权变为其中的一半,求最短路。
输入:
4 4 1
1 2 4
4 2 6
1 3 8
3 4 8
输出:
7
建图:
我们假设现在在第i层,点u和点v之间有一条权值w的边,对于下一层,即i+1层,u'与v'之间仍是有一条权为w的边,且对于u与v'之间应该加上一条边权为w/2的边。所以如果每一层有m条边,第i层和第i+1层之间也一定是有m条边。显然层数就是k,每上下层都有一个w/2,走到第k层的终点即可完成最小用时。
代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <limits.h>
using namespace std;
typedef long long ll;
const int N=2e6;
struct edge{
int from;
int to;
int dis;
int next;
}e[N];
int head[N],cnt;
int u,v,w;
int n,m,k;
int s,t;
void add(int u,int v,int w)
{
++cnt;
e[cnt].from = u;
e[cnt].to = v;
e[cnt].dis = w;
e[cnt].next = head[u];
head[u] = cnt;
}
int mapp[N];
bool vis[N];
queue<int> q;
void SPFA(int u)
{
memset(vis,0,sizeof(vis));
memset(mapp,0x3f,sizeof(mapp));
q.push(u); vis[u] = true;
mapp[u] = 0;
while(!q.empty())
{
int x = q.front();
vis[x] = false;
q.pop();
for(int i=head[x];i;i=e[i].next)
{
int y = e[i].to;
if(mapp[y] > mapp[x] + e[i].dis)
{
mapp[y] = mapp[x] + e[i].dis;
if(vis[y] == false)
{
vis[y] = true;
q.push(y);
}
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
//scanf("%d%d",&s,&t);
s = 1;t = n;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
for(int j=1;j<=k;j++)
{
add(u+j*n,v+j*n,w);
add(v+j*n,u+j*n,w);
add(u+(j-1)*n,v+j*n,w/2);
add(v+(j-1)*n,u+j*n,w/2);
}
}
for(int i=1;i<=k;i++)
add(t+(i-1)*n,t+i*n,0);
SPFA(s);
printf("%d",mapp[t+k*n]);
return 0;
}
时间复杂度:
SPFA O(n*m) 不会超时
例题2
洛谷P4568 JLOI2011飞行路线
题意:
只是例题一的w/2,变为了0
输入:
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100
输出:
8
数据范围:
2 \(\leqslant\) n \(\leqslant\) \(10^4\), 1 \(\leqslant\) m \(\leqslant\) \(5*10^4\)
算法:
SPFA会超时,所以我们用堆优化的Dijkstra
代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int N=5e6;
struct edge{
int from;
int to;
int dis;
int next;
}e[N];
struct node{
int dis;
int pos;
bool operator <(const node &x)const
{
return x.dis < dis;//权值从小到大排序
}
};
priority_queue<node> q;
int mapp[N];
bool vis[N];
int head[N],cnt;
int u,v,w;
int n,m,k,s,t;
void add(int u,int v,int w)
{
++cnt;
e[cnt].from = u;
e[cnt].to = v;
e[cnt].dis = w;
e[cnt].next = head[u];
head[u] = cnt;
}
void Dijkstra(int u)
{
memset(mapp,0x3f,sizeof(mapp));
mapp[u]=0;
q.push((node){0,u});
while(!q.empty())
{
node p;
p=q.top();
q.pop();
int x = p.pos,d = p.dis;
if(vis[x] == true) continue;
vis[x] = true;
for(int i=head[x];i;i=e[i].next)
{
int y=e[i].to;
if(mapp[y]>mapp[x]+e[i].dis)
{
mapp[y]=mapp[x]+e[i].dis;
q.push((node){mapp[y],y});
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
scanf("%d%d",&s,&t);
//s = 1;t = n;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
for(int j=1;j<=k;j++)
{
add(u+j*n,v+j*n,w);
add(v+j*n,u+j*n,w);
add(u+(j-1)*n,v+j*n,0);
add(v+(j-1)*n,u+j*n,0);
}
}
for(int i=1;i<=k;i++)
add(t+(i-1)*n,t+i*n,0);
Dijkstra(s);
printf("%d",mapp[t+k*n]);
return 0;
}
四倍经验
洛谷P2939 USACO09FEBRevamping Trails G
简直一模一样就不放代码了
洛谷P1948 USACO08JANTelephone Lines S
根据题意改一处代码即可
代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int N=6e6;
struct edge{
int from;
int to;
int dis;
int next;
}e[N];
struct node{
int dis;
int pos;
bool operator <(const node &x)const
{
return x.dis < dis;//权值从小到大排序
}
};
priority_queue<node> q;
int mapp[N];
bool vis[N];
int head[N],cnt;
int u,v,w;
int n,m,k,s,t;
void add(int u,int v,int w)
{
++cnt;
e[cnt].from = u;
e[cnt].to = v;
e[cnt].dis = w;
e[cnt].next = head[u];
head[u] = cnt;
}
void Dijkstra(int u)
{
memset(mapp,0x3f,sizeof(mapp));
mapp[u]=0;
q.push((node){0,u});
while(!q.empty())
{
node p;
p=q.top();
q.pop();
int x = p.pos,d = p.dis;
if(vis[x] == true) continue;
vis[x] = true;
for(int i=head[x];i;i=e[i].next)
{
int y=e[i].to;
if(mapp[y]>max(mapp[x],e[i].dis))
{
mapp[y]=max(mapp[x],e[i].dis);
q.push((node){mapp[y],y});
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
//scanf("%d%d",&s,&t);
s = 1;t = n;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
for(int j=1;j<=k;j++)
{
add(u+j*n,v+j*n,w);
add(v+j*n,u+j*n,w);
add(u+(j-1)*n,v+j*n,0);
add(v+(j-1)*n,u+j*n,0);
}
}
for(int i=1;i<=k;i++)
add(t+(i-1)*n,t+i*n,0);
Dijkstra(s);
if(mapp[t+k*n] == 1061109567) printf("-1\n");
else printf("%d",mapp[t+k*n]);
return 0;
}
NOIP2009 提高组 最优贸易
输入
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
输出
5
分析
可以构造如下分层图
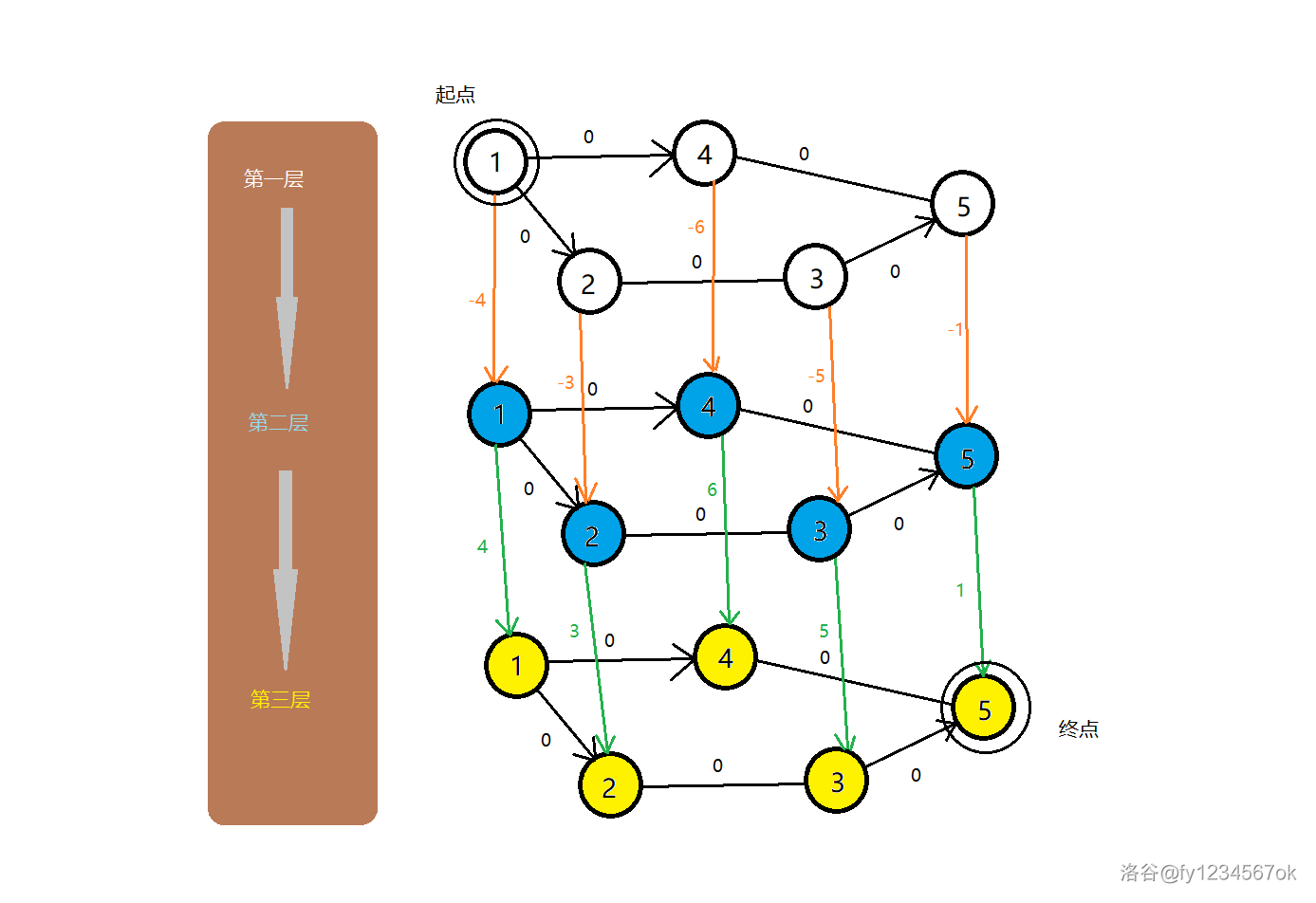
假设第一层普通的图,那么第二层表示只买,第三层只卖。那么答案就是1-n*3的最长路,因为有负边权,用SPFA。详细看代码
代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <limits.h>
using namespace std;
typedef long long ll;
const int N=2e6;
struct edge{
int from;
int to;
int dis;
int next;
}e[N];
int head[N],cnt;
void add(int u,int v,int w)
{
++cnt;
e[cnt].from = u;
e[cnt].to = v;
e[cnt].dis = w;
e[cnt].next = head[u];
head[u] = cnt;
}
int n,m;
int a[N];
int u,v,w;
int mapp[N];
bool vis[N];
queue<int> q;
void SPFA(int u)
{
for(int i=1;i<=3*n;i++)
mapp[i] = -10000;
memset(vis,0,sizeof(vis));
mapp[u] = 0; vis[u] = true;
q.push(u);
while(!q.empty())
{
int x = q.front();
vis[x] = false;
q.pop();
for(int i=head[x];i;i=e[i].next)
{
int y = e[i].to;
if(mapp[y] < mapp[x] + e[i].dis)
{
mapp[y] = mapp[x] + e[i].dis;
if(vis[y] == false)
{
vis[y] = true;
q.push(y);
}
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,0);
add(u+n,v+n,0);//每一层之间的所有点以边权为0连接
add(u+2*n,v+2*n,0);
if(w == 2)
{
add(v,u,0);
add(v+n,u+n,0);
add(v+2*n,u+2*n,0);
}
}
for(int i=1;i<=n;i++)
{
add(i,i+n,-a[i]);//层与层之间连边
add(i+n,i+2*n,a[i]);
}
SPFA(1);
printf("%d",mapp[3*n]);
return 0;
}
P5663 CSP-J2019加工零件
输入
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2
输出
No
Yes
No
Yes
No
Yes
代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
typedef long long ll;
const int N=3e6;
struct edge{
int from;
int to;
int dis;
int next;
}e[N];
int head[N],cnt;
void add(int u,int v,int w)
{
++cnt;
e[cnt].from = u;
e[cnt].to = v;
e[cnt].dis = w;
e[cnt].next = head[u];
head[u] = cnt;
}
int mapp[N];
bool vis[N];
queue<int> q;
void SPFA(int u)
{
memset(mapp,0x3f,sizeof(mapp));
memset(vis,0,sizeof(vis));
mapp[u] = 0; vis[u] = true;
q.push(u);
while(!q.empty())
{
int x = q.front();
vis[x] = false;
q.pop();
for(int i=head[x];i;i=e[i].next)
{
int y = e[i].to;
if(mapp[y] > mapp[x] + e[i].dis)
{
mapp[y] = mapp[x] + e[i].dis;
if(vis[y] == false)
{
vis[y] = true;
q.push(y);
}
}
}
}
}
int n,m,p,u,v;
int a,L;
int main()
{
cin>>n>>m>>p;
//设i号节点的偶节点为i,奇节点为i+n
//偶节点含义从1到该节点距离(永远)为偶数的节点;
//奇节点定义从1到该节点距离(永远)为奇数的节点;
for(int i=1;i<=m;i++)
{
cin>>u>>v;
add(u,v+n,1);
add(v+n,u,1);
add(u+n,v,1);
add(v,u+n,1);
}
//编号为a的工人想生产一个第L阶段的零件需要1号提供原材料
//等价于从1号到a的最短路径<= L && 与L的奇偶性相同,即只要大于最短路&&与其奇偶性相同的都可以构造出来
//因为来回走一条路径会使路径值+2,
SPFA(1);
for(int i=1;i<=p;i++)
{
cin>>a>>L;
if(L&1)//为奇数
{
if(mapp[a+n] <= L)//奇数路径
puts("Yes");
else puts("No");
}
else
{
if(mapp[a] <= L)//偶数路径
puts("Yes");
else puts("No");
}
}
/*cout<<endl;
for(int i=1;i<=2*n;i++)
{
cout<<mapp[i]<<" ";
}*/
return 0;
}
P3119 USACO15JANGrassCownoisseurG
题意
约翰有n块草场,编号1到n,这些草场由若干条单行道相连。奶牛贝西是美味牧草的鉴赏家,她想到达尽可能多的草场去品尝牧草。
贝西总是从1号草场出发,最后回到1号草场。她想经过尽可能多的草场,贝西在通一个草场只吃一次草,所以一个草场可以经过多次。因为草场是单行道连接,这给贝西的品鉴工作带来了很大的不便,贝西想偷偷逆向行走一次,但最多只能有一次逆行。问,贝西最多能吃到多少个草场的牧草。
输入格式
第一行:草场数n,道路数m。
以下m行,每行x和y表明有x到y的单向边,不会有重复的道路出现。
输出格式
一个数,逆行一次最多可以走几个草场。
输入
7 10
1 2
3 1
2 5
2 4
3 7
3 5
3 6
6 5
7 2
4 7
输出
6
分析
首先有环,我们可以用tarjan缩点,缩完点后的点权为连通块内点的个数,跑一个最长路。
问题在于可以逆行一次。
我们可以建造分层图,来达到逆行一次的效果。
先建一个一模一样的图,两个图的点权一致,在连一条v,u+n的边(这里的n表示缩完点后点的数量),
spfa跑一个最长路。取mapp[color[1]]和mapp[color[1] + sccnt]的较大值即可;
注意起点题目中虽然是一号点,但我们要从一号点对应的连通块编号出发,也就是color[1],初始点权要设置为0.(从一号点出发,但它不吃一号点的草)。
代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <stack>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 2e6;
int n,m;
struct edge{
int from;
int to;
int dis;
int next;
}e[N];
int head[N],cnt;
void add(int u,int v)
{
++cnt;
e[cnt].from = u;
e[cnt].to = v;
e[cnt].next = head[u];
head[u] = cnt;
}
int low[N],pre[N],t,siz[N];
int sccnt,color[N],from[N],to[N];
bool vis[N];
stack<int> q;
void tarjan(int u)
{
low[u] = pre[u] = ++t;
vis[u] = true;
q.push(u);
for(int i=head[u];i;i=e[i].next)
{
int v = e[i].to;
if(pre[v] == 0)
{
tarjan(v);
low[u] = min(low[u],low[v]);
}
else if(vis[v] == true)
{
low[u] = min(low[u],pre[v]);
}
}
if(pre[u] == low[u])
{
int w;
sccnt++;
do
{
w = q.top();
q.pop();
vis[w] = false;
color[w] = sccnt;
siz[sccnt]++;
}while(u != w);
}
}
int mapp[N];
queue<int> qe;
void SPFA(int u)
{
memset(mapp,-100,sizeof(mapp));
memset(vis,0,sizeof(vis));
mapp[color[u]] = 0;
vis[color[u]] = true;
qe.push(color[u]);
while(!qe.empty())
{
int x = qe.front();
vis[x] = false;
qe.pop();
for(int i=head[x];i;i=e[i].next)
{
int y = e[i].to;
if(mapp[y] < mapp[x] + siz[y])
{
mapp[y] = mapp[x] + siz[y];
if(vis[y] == false)
{
vis[y] = true;
qe.push(y);
}
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
from[i] = u,to[i] = v;
add(u,v);
}
for(int i=1;i<=n;i++)
{
if(pre[i] == 0)
tarjan(i);
}
//cout<<endl;
memset(head,0,sizeof(head)); cnt = 0;memset(&e,0,sizeof(e));
//for(int i=1;i<=sccnt;i++)
//cout<<siz[i]<<" ";
//cout<<endl;
for(int i=1;i<=m;i++)
{
int u = from[i],v = to[i];
if(color[u] != color[v])
{
//cout<<u<<" "<<v<<endl;
//cout<<color[u]<<" "<<color[v]<<endl;
//cout<<endl;
add(color[u],color[v]);
add(color[u] + sccnt,color[v] + sccnt);
siz[color[u] + sccnt] = siz[color[u]];
siz[color[v] + sccnt] = siz[color[v]];
add(color[v],color[u]+sccnt);
}
}
SPFA(1);
printf("%d",max(mapp[color[1]],mapp[color[1] + sccnt]));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号