差分约束系统
【模板】差分约束
前置知识
想要做对差分约束，负环判定这个知识肯定是要会的，不会的可以看我的另一篇博客qwq
另外，若干您不想看题解，也可以直接看判断负环的模板题P3385
差分约束系统
（以下内容部分摘自《算法竞赛进阶指南》）
- 差分约束系统
差分约束系统是一种特殊的\(N\)元一次不等式
它包含\(N\)个变量\(X_1\) ~ \(X_n\)以及\(M\)各约束条件，每个约束条件都是由两个变量做差构成的（所以是差分嘛！），形如\(X_i-X_n≤C_k\)，其中\(C_k\)是常数（可以是负数也可以是非负数），\(1≤i,j≤N，1≤k≤M\)
我们要解决的问题就是：求一组解\(X_1=a_1,X_2=a_2···X_n=a_n\)，使所有约束条件都得到满足
- 转换思想
差分约束系统的每个约束条件\(X_i-X_j≤C_k\)可以变形为\(X_i≤X_j+C_k\)
有没有觉得有那么一点点的熟悉？
嗯...和求解单源最短路中的三角形不等式\(dis[i]≤dis[j]+e[i].val\)（\(dis[i]-dis[j]≤e[i].val\)）非常相似
因此可以三角形不等式推广：把每个变量\(X_i\)看作有向图中的一个节点\(i\)，对于每个约束条件\(X_i-X_n≤C_k\)，从节点\(j\)向节点\(i\)连一条长度为\(C_k\)的有向边
现在来看下面给出的这张图，来讲解一下差分约束中的最短路和最长路（可能有点绕，但是图很好理解）：
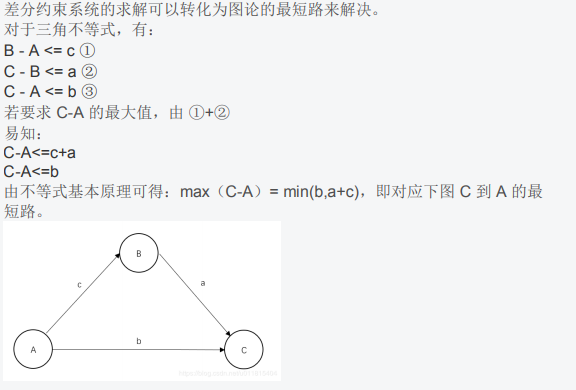
从这张图中的例子，我们不难得出（重点啊）：
-
差分约束跑最短路，跑出的结果是所有解中的最大解
-
差分约束跑最长路，跑出的结果是所有解中的最小解
但是，最短路和最长路也是可以互相转换的，什么意思？（需要掌握）
在某些题目中，约束条件形如\(x_i-X-j≥C_k\)，我们有两种方式解决：
-
可以从\(j\)到\(i\)连一条长度为\(C_k\)的有向边，然后计算单源最长路，若图中有正环则无解
-
我们也可以把约束条件转化成\(X_j-X_i≤-C_k\)，再按单源最短路进行计算
- 解题模型
PS：差分约束是有多组解的，但是题目一般只会要求输出其中任意一种
-
建立“超级源点0”，将\(0\)与每个点\(i\)连一条长为\(0\)的边，然后以\(0\)为起点求单源最短路
-
不建立“超级源点”，将每一个点都入队然后去跑最短路
若图中存在负环，则给定的差分约束系统无解；否则\(X_i=dis[i]\)就是差分约束系统的一组解
例题代码
现在给出这道模板题的代码（如下是\(SPFA\)版本的，下面会给出\(Ford\)版本的函数段）：
#include <bits/stdc++.h>
using namespace std;
queue<int> q;
int n,m,u,v,w,tot;
int dis[200010],vis[200010],cnt[200010],head[200010];
struct node {
int to,net,val;
} e[200010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline bool spfa() {
for(register int i=0;i<=n;i++) {
vis[i]=0;
dis[i]=20050206;
}
dis[0]=0;
vis[0]=1;
q.push(0);
while(!q.empty()) {
int x=q.front();
q.pop();
vis[x]=0;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
if(cnt[v]>=n) return false;
if(!vis[v]) {
vis[v]=1;
cnt[v]++;
q.push(v);
}
}
}
}
return true;
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&w);
add(v,u,w);
}
for(register int i=1;i<=n;i++) add(0,i,0);
if(spfa()==false) puts("NO");
else {
for(register int i=1;i<=n;i++) printf("%d ",dis[i]);
}
return 0;
}
下面是\(Ford\)版本的函数段，其他的和上面的没什么区别
inline bool ford() {
for(register int i=0;i<=n;i++) dis[i]=20050206;
dis[0]=0;
for(register int i=0;i<n;i++) {
for(register int j=1;j<=tot;j++) {
if(dis[e[j].fro]+e[j].val<dis[e[j].to]) {
dis[e[j].to]=dis[e[j].fro]+e[j].val;
}
}
}
for(register int i=1;i<=tot;i++) {
if(dis[e[i].fro]+e[i].val<dis[e[i].to]) return false;
}
return true;
}
好题推荐
-
洛谷P3275 糖果 （差分约束还是算经典的一道题，不过也可以缩点+拓扑A掉）
-
洛谷P2294 狡猾的商人 （思路巧妙的差分约束/并查集/贪心/DP（后两种比较玄学））
更新于：2020.7.3——狡猾的商人题解
最后，关于上面其他好题的题解我会陆陆续续更新在我的博客中，欢迎大家来踩qwq
如果有任何不懂或是我的题解有误的，欢迎大家在评论区留言，我会及时回复、改正，谢谢大家啊orz
