行列式, 偏序与杨表: 代数的抻直律

多项式环, \(k[X_1,\dots,X_n]\), 本身是一个相对来说比较 "简单" 的事物. 这里说简单的意思是, 对于 \(k[X_1,\dots,X_n]\) 本身的每一个元素, 我们有一个简单的 "描述" 它的方法: 每个元素都有唯一的方式, 写作单项式的线性组合, 而单项式都写作 \(X_1^{i_1} \cdots X_n^{i_n}\). 而我们一旦转换到它的一个商环或者自环, 情况就很容易变得极为复杂了.

一个具体的例子是所谓的行列式环 (determinantal ring) 问题. 考虑总共 \(n\times m\) 个变量 \(X_{ij} \in k\), 我们想象它组成一个 \(n\times m\) 的矩阵. 我们只想考虑这个矩阵的秩 \(<r\) 的情况. 线性代数的知识告诉我们, 这个性质可以被多项式方程刻画:

定理. 矩阵 \(X\) 的秩 \(<r\), 当且仅当所有大小为 \(r\) 的子集 \(S\subseteq [n], T\subseteq [m]\), 子式 \(\det(X_{S, T}) = 0\).

我们又知道, 根据矩阵秩的某种定义, 一个矩阵的秩 \(< r\) 当且仅当存在两个矩阵 \(U\in k^{n\times (r-1)}, V \in k^{(r-1)\times m}\), 使得 \(X=UV\).

我们记所有秩 \(<r\) 的矩阵空间为 \(X_{<r} \subset k^{n\times m}\), 那么前面的定理告诉我们的事实就是, \(X_{<r}\) 是一个代数集, 可以写作 \(X_{<r} = V(I_r)\), 其中 \(I_r\) 就是所有 \(r\) 阶子式生成的多项式理想. 而矩阵的另一种定义告诉我们, 这个集合 \(X_{<r}\) 是某个多项式映射

\[k^{n\times (r-1)}\times k^{(r-1)\times m} \to k^{n\times m} \]

的像. 由于这个映射的原像是不可约的, 那么 \(X_{<r}\) 本身也不可约. 这应该告诉我们一个基本事实: 这个 \(X_{<r}\) 的坐标环, 也即多项式对 \(X_{<r}\) 满足的所有理想的商环 \(k[X_{ij}]/I(X_{<r})\), 应该是整环, 也即 \(I(X_{<r})\) 是一个素理想. 但是这就有了一个问题---这并没有完全告诉我们关于原本的理想 \(I_r\) 的信息. 根据 Hilbert 零点定理, 我们知道 \(I(X_{<r}) = \sqrt{I_r}\). 但是 \(I_r\) 到底是不是 \(\sqrt{I_r}\) 呢? Eagon 和 Northcott 对此给出了肯定性的答案:

定理 (Eagon–Northcott). 对于任何整环 \(B\), 多项式环 \(B[X_{ij}]\) 上的 \(r\) 阶子式生成的理想 \(I_r\) 总是素理想.

他们是用了同调代数的方法才得出这一结果的. 后来, 人们希望发展一个更加显式的理论用来研究行列式环.

某种意义上说, 就是想要给出一种更加直观的证明: 行列式环是一个商环, 我们能不能规定某种每个等价类里找出一个 "典范" 的代表元呢? 证明一个理想 \(\mathfrak p\) 是素理想, 无非是说 \(A/\mathfrak p\) 是整环, 也即 \(a,b\neq 0\implies ab\neq 0\). 如果我们能有某种 "典范" 的代表元, 在两个元素相乘的时候又能论证乘法的结果依然有某个 "最大项" 保留着, 那自然就证明了环是整环了.

这个想法在一般意义上当然是极为困难的, 所以目前对于一般的多项式理想, 其素性测试---由 Gröbner 基给出---复杂度高达 EXPSPACE (指数空间).

不过出于一些 (来自不变量理论的) 动机, 人们实际上成功在行列式环上得到了一个这么相当组合的理论, 称作 "抻直律" 的理论. 它一开始由 Hodge 提出, 然后由 de Cocini–Eisenbud–Procesi 和 Doubilet–Rota–Stein 将行列式的情况完善.

什么是抻直律

一个环 \(A\), 我们说它是分次的, 如果可以把它写成 \(A_0, A_1,\dots, A_n, \dots\) 的部分, 且 \(A\) 的所有元素都能写成这些 \(A_i\) 唯一的线性组合的形式, 也即 \(A=\bigoplus_{d\geq 0} A_d\). 两个次数为 \(d, e\) 的元素乘起来应该是 \(d+e\) 次的 (虽然也可以是 \(0\)): \(A_d A_d \subset A_{d+e}\).

我们今天只考虑 \(A_0=k\) 的情况. 比如说多项式环 \(k[X_1,\dots,X_n]\) 就可以把所有齐次 \(d\) 次多项式写成部分 \(A_d\).

我们首先给出抻直律的一般定义. 一个分次的环 \(A\), 我们说它是一个有抻直律的代数 (Algebra with Straightening Law, ASL), 如果我们可以给出一个有限集 \(P\subset A\), 这个有限集每个元素都是次数大于 \(0\) 的齐次元素. 进一步地, 要给 \(P\) 赋予一个偏序关系:

• 对于任何一条链 \(\alpha_1 \leq \cdots \leq \alpha_n\), 我们管这样的连乘积 \(\alpha_1 \cdots \alpha_n\) 叫一个标准单项式 (standard monomial).
• 我们要求全体标准单项式线性无关. 但是它们组成的单项式 (也就是乘的时候可以不可比) 张成整个 \(A\).
• (抻直律) 如果 \(\alpha, \beta\) 不可比, 那么乘积 \(\alpha \beta\) 需要可以写为一些标准单项式的线性组合 \(\sum c_\mu \mu\), 其中每一项 \(\mu = \gamma_1 \cdots \gamma_m\) 需要满足首项 \(\gamma_1\leq \alpha\) 且 \(\gamma_1 \leq \beta\) (这其实等价于严格小于). 注意如果 \(\alpha \beta = 0\), 这也是自动满足条件的.

我们先看第一个平凡的例子: 对于多项式环 \(k[X_1,\dots,X_n]\), 偏序

\[X_1 \leq \cdots \leq X_n \]

就是一个 ASL.

我们接下来看第二个例子: 它仍然是四个变量的多项式环, 但是我们给它一个不同的抻直律, 如图所示:

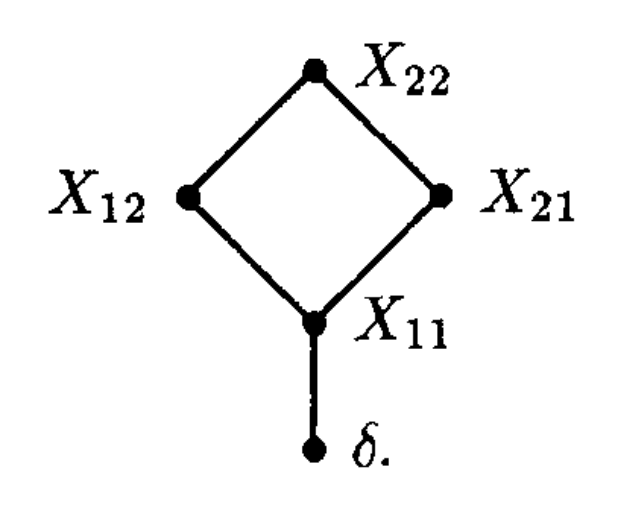
(截自 Bruns & Vetter, Determinantal Rings)

其中 \(\delta\) 是矩阵 \(X_{ij}\) 的行列式, 也即 \(\delta = X_{11}X_{22} - X_{12} X_{21}\). 换句话说, 抻直律由关系

\[X_{12} X_{21} = X_{11}X_{22} - \delta \]

给出. 显然除了标准单项式线性无关这点需要花力气验证, 其他都是比较显然的. 不过由于不是重点, 我们现在并不验证这个例子.

一个基本事实是, 抻直律的基本要求保证了标准单项式不仅彼此线性无关, 而且刚好构成了 \(A\) 的一组基: 直观上说, 读者只需考虑任何两个标准单项式相乘之后何以仍然表为一系列标准单项式的线性组合. 通过运用抻直律, 每次可以 "解决" 一个不可比的部分. 而抻直律里微妙的条件 \(\gamma_1 < \alpha, \beta\), 结合次数的良定义, 可以让这个过程总是递降的.

这验证了为什么它被称作 straightening: 把原来不是链的乘积抻直.

接下来, 我们来看一个具体的例子.

Plüker 代数的抻直律

我们现在不考虑子式生成的理想, 而是生成的子代数. 假设 \(n\geq m\), 我们考虑这么一个特殊例子: 恰所有 \(m\) 阶子式, 这些子式生成的子代数 \(A\subset k[X_{ij}]\) 我们称为 Plüker 代数.

对于 \(A\) 的生成元, 我们有一个自然而然的表达方式: 选取 \(a_1,\dots,a_m \in [n]\), 我们用方括号括住序列

\[[a_1,\dots,a_m] = \det(X_{a_1,\dots,a_m}) \]

表示按顺序选取出这些行, 组成的矩阵求行列式. 显然, 我们实际上只需要取 \(a_1 < \cdots < a_m\) 的情况就可以了, 我们一般情况下允许 \(a\) 是任何序列, 但对于 \(a\in P\) 我们假设此时一定有 \(a\) 严格单调. 对于 \(P\) 上的偏序, 我们直接让它逐点比较, 也即 \(a\leq b\) 当且仅当 \(a_i\leq b_i\) 对所有 \(i\) 成立.

现在, 让我们来先尝试验证抻直律吧! 为此, 我们需要先找出一些子式的抵消规则. 显然这些项在刚好张成了 "一次" 的情况, 那在 "二次" 就会开始产生 "合冲" (syzygy) 了.

定理 (Plüker 关系). 对于任何 \(a_1,\dots,a_{k}\), \(c_{k+2}, \dots, c_{m}\) 和 \(b_1,\dots,b_{m+1}\), 有

\[\sum_{\sigma \in S_{m+1}} (-1)^\sigma [a_1,\dots,a_k,b_{\sigma(1)},\dots,b_{\sigma(m-k)}] \cdot [b_{\sigma(m-k+1)},\dots,b_{\sigma(m+1)}, c_{k+2},\dots,c_m] = 0. \]

证明. 我们现在把问题想象成一个一般的矩阵问题 \(\sum_\sigma (-1)^{\sigma} \det(A | B_{\sigma(1,\dots,m-k)})\det(B_{\sigma(m-k+1,\dots,m+1)}|C)\). 现在假设 \(A,C\) 都已经固定了, 这就是一个只输入矩阵 \(B\), 输出 \(k\) 的问题.

这个映射 \(k^{(m+1)\times m}\to k\) 是交错线性的: 如果 \(B\) 有两行相等, 那么在求和里, 如果这两行落在同一个 \(\det\) 中, 那就直接为 \(0\). 如果落在两个不同的 \(\det\) 中, 那么交换它们配对, 置换的符号 \((-1)^\sigma\) 把它们抵消了.

一个 \((k^m)^{m+1} \to k\) 的交错线性映射只能是零映射, 所以求和结果必是 \(0\). \(\square\)

显然上面的求和每一项都被重复数了 \((m-k)! \cdot (k+1)!\) 次, 我们去重之后会得到一个每个单项式系数都是 \(\pm 1\) 的关系:

\[\sum_{S\sqcup T = [m+1]} (-1)^{\operatorname{inv}(S, T)} [a,b_S] \cdot [b_T, c] = 0. \]

现在我们就可以构造抻直律了! 如果 \(u,v\in P\) 不可比, 那么我们不妨假设存在 \(k\) 使得 \(u_i \leq v_i\) 对 \(i \leq k\) 都成立, 但 \(u_{k+1} > v_{k+1}\). 注意此时就有了一条新的链 \(v_1<\dots <v_{k+1} < u_{k+1} < \cdots < u_m\).

对于这种问题来说不如举个实际的例子, 我们考虑 \([1, 4, 6] \cdot [2, 3, 5]\). 现在不可比的地方出现在第二个位置:

\[[1, {\bf 4}, {\bf 6}] \cdot [{\bf 2}, {\bf 3}, 5] \]

那么 Plüker 关系让我们枚举把 \(2, 3, 4, 6\) 填进 \([1, -, -]\cdot [-, -, 5]\) 的方式, 我们会得到:

\[[1, 4, 6] [2, 3, 5] - [1,3,6][2,4,5] + [1,2,6][3,4,5] + [1,3,4][2,6,5] - [1,2,4][3,6,5] + [1,2,3][4,6,5] = 0. \]

现在有些项都不是单调递增的下标了, 我们调整, 得到

\[[1, 4, 6] [2, 3, 5] - [1,3,6][2,4,5] + [1,2,6][3,4,5] - [1,3,4][2,5,6] + [1,2,4][3,5,6] - [1,2,3][4,5,6] = 0. \]

后三项都是标准单项式, 但是 \([1,3,6][2,4,5], [1,2,6][3,4,5]\) 依然是不可比的乘积. 我们需要递归地拆下去. 但是注意到:

• Plüker 关系里产生的其他项 \(u'v'\), 总是分别改进了 \(u\) 和 \(v\): \(u'\leq u\) 且 \(v' \geq v\). 所以这个过程一定是 "递降的", 会终止成一堆标准单项式.
• 但是怎么证明最后每个标准单项式 \(ab\) (\(a\leq b\)) 都满足 \(a\leq u, v\) 呢? 这里我们先假设已经证明了标准单项式是线性无关的 (待会就证), 那么我们观察一下我们已经知道了什么: 我们知道 \(u\cdot v\) 已经可以写成一些标准单项式的线性组合, 这个线性组合是唯一的, 而前面的归纳过程中保证了 \(a\leq u\) 是成立的. 那么我们可以用完全相同的道理跑一遍 \(v\cdot u\) 的展开式, 说明最后得到的标准单项式的每一项也必然是 \(\leq v\) 的!

现在我们证明线性无关性. 其实做法也相当直接: 我们给单项式 (\(X_{ij}\) 为基单项式而不是子式!) 规定一个字典序关系, 然后直接证明不同的标准单项式的 "字典序" 最大的那个单项式互不相同. (实际上规定一个好的序关系, 也是 Gröbner 基里的常规操作)

为了方便, 我们希望这个序关系是保乘法的: 如果两个单项式 \(X^I \leq X^J\), 那么 \(X^I \cdot X^K \leq X^J \cdot X^K\), 这样一来任何两个多项式 \(f\cdot g\) 的最高此项就是 \(f, g\) 各自最高次项的乘积了, 对我们的计算会方便很多.

答案基本上就是你第一个想到该试什么: 直接规定 \(X_{11} > X_{12} >\dots> X_{1m} > X_{21} > \cdots > X_{nm} > 1\), 比较字典序! 那么对于任何一个子式, 就自然有

\[[a_1,\dots,a_m] = X_{a_1 1} X_{a_2 2} \cdots X_{a_m m}. \]

所以一个标准单项式 \(a^1\cdots a^k\) 的最高次项就是

\[\prod_{i=1}^k (X_{a^i_1 1} \cdots X_{a^i_m m})= \prod_{i=1}^k \prod_{j=1}^m X_{a_{j}^i j}, \]

因为 \(a_{j}^i\) 固定 \(j\) 关于 \(i\) 递增, 我们自然可以从这个最高此项直接把 \(a^1,\dots,a^k\) 本身读出来.

综上, 我们验证了 Plüker 代数的所有抻直律.

定理. Plüker 代数是一个 ASL.

杨表

上面的刻画给了我们一个数 Plüker 代数 \(A\) 的 \(d\) 次部分 \(A_d\) 的维度的直接方法: 它就是递增序列 \(a^1 \leq \cdots\leq a^k \in P\) 的数量. 我们知道每个 \(a^i\) 都是一个长为 \(m\) 的数组, 如果把它们排成一列呢?

a[1,1] < ... < a[1, m]
 <=              <=
a[2,1] < ... < a[2, m]
...

我去, 这不是我们半标准杨表 (semi-standard Young tableaux) 吗? 不过准确说半标准杨表的定义是按行不严格单调递增, 按列严格递增. 所以我们要做个转置.

定理. \(n\times m\) 的 Plüker 代数的 \(d\) 次部分维数 \(\dim_k A_d\) 等于 \(m\times k\) 形状的, 值域为 \(n\) 的半标准杨表填数方案.

这个填数方案的公式是熟知的, 我就不贴出来了.

事实上, 杨表和多项式环有一个更加细致的对应关系. 这个关系本质上是通过考虑如下增广矩阵实现的:

\[\begin{pmatrix} X\\ I \end{pmatrix} \]

这个矩阵的 \(m\) 阶子式, 事实上实现了 \(X\) 矩阵的所有可能子式: 如果对于大小相同的 \(S\subset [n]\) 和 \(T\subset [m]\), 子式 \(\det X_{ST}\) 等价于选取 \(S\) 这些行, 加上 \(I\) 里的 \(T\) 的补集那些行, 就相当于去掉了对应的 \(X\) 的列. 我们这里略过细节分析, 这个增广矩阵沿用前面的 ASL, 可以转写为如下的形式 (不妨仍然设 \(n\geq m\)):

定理 (Doubilet–Rota–Stein). 我们记有限集 \(P\) 为如下所有序列: \([a_1,\dots,a_r \mid b_1,\dots,b_r]\), 满足 \(a,b\) 都是严格递增序列, 分别值域为 \(n, m\). 其中 \(r\) 可以取值为任何不超过 \(m\) 的正整数.

这个序列代表的就是取出 \(X\) 对应的位置子矩阵求子式. 我们给 \(P\) 赋予如下偏序:

• \([a_1,\dots,a_r \mid b_1,\dots,b_r] \leq [c_1,\dots,c_s \mid d_1,\dots,d_s]\), 当且仅当 \(r\geq s\) 且 \(a_i\leq c_i, b_i\leq d_i\) 对所有 \(i\leq s\) 都成立.

这个偏序是整个多项式环 \(k[X_{ij}]\) 的一个抻直律.

对于一个整数拆分 \(\lambda\), 以其为形状的一对杨表 (bitableaux) \((S \mid T)\), 两个表所填的数的值域分别为 \(n, m\), 这对杨表定义出双行列式 (bideterminant), 为每行所取出子式的乘积: \((S\mid T)(X) = \prod_i \det(X_{S_i T_i})\).

那么偏序 \(P\) 对应的全体标准单项式恰为双行列式 \((S\mid T)(X)\) 中 \(S, T\) 的转置皆为半标准杨表的情况, 称之为标准双行列式 (standard bideterminant). 也就是说, 标准双行列式恰构成多项式环 \(k[X_{ij}]\) 的一组基.

其实一开始举的第二个例子就是 \(2\times 2\) 矩阵的抻直律.

对于大家喜闻乐见 (并不) 的 Pffafian, 也有一个类似的抻直律 (Abeasis–Del Fra), 在这里就不介绍了.