二分查找
二分模板
算法思路:假设目标值在闭区间[l, r]中, 每次将区间长度缩小一半,当l = r时,我们就找到了目标值。
版本1
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时,其更新操作是r = mid或者l = mid + 1;计算mid时不需要加1
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
版本2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或者l = mid;此时为了防止死循环,计算mid时需要加1。
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
参考:https://www.acwing.com/blog/content/31/
版本3
循环条件:l < r - 1,l = mid, r = mid
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l < r - 1){
int mid = l + (r - l) / 2;
if (nums[mid] >= target)
r = mid;
else
l = mid + 1;
}
if(nums[r] < target)
return r;
else if(arr[l] > k)
return l;
else return target - nums[l] < nums[r] - k ? l : r;
}
为什么不用mid = (left+right)/2 而用mid = left + (right-left)/2
因为left和right都是signed int类型,最多表示到2^31 - 1, 如果left=1, right = 2^31-1. 那么left+right就等于2^31, 超出signed int的上界2^31-1的限制, 发生数据溢出。 left+(right-left) 实际上限制了相加的两个数字的大小,不会造成溢出
Leetcode704 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
/*
* @lc app=leetcode.cn id=69 lang=cpp
*
* [69] x 的平方根
*/
// @lc code=start
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x/2+1;
while(l<r){
//int mid = l + (long long)r + 1 >> 1;
int mid = l + ((long long)r - l + 1) / 2;
//if (mid * mid > x) 可能会溢出
if (mid > x / mid)
r = mid - 1;
else
l = mid;
}
return l; //l == r
}
};
// @lc code=end
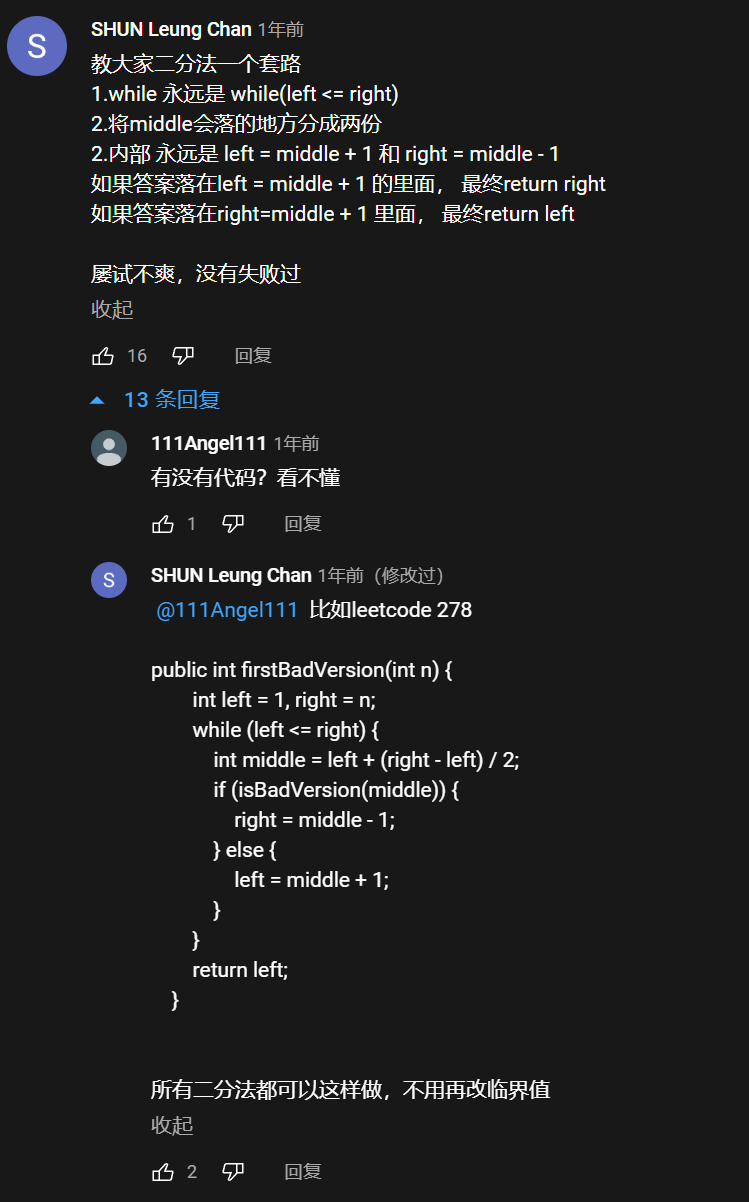
看YouTube上评论区一兄弟的方法,还是挺好用的
/*
* @lc app=leetcode.cn id=35 lang=cpp
*
* [35] 搜索插入位置
*/
// @lc code=start
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l <= r){
int mid = l + (r - l) / 2;
if (nums[mid] >= target)
r = mid - 1;
else
l = mid+1;
}
return l;
}
};
// @lc code=end
Leetcode34 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
source code
/*
* @lc app=leetcode.cn id=34 lang=cpp
*
* [34] 在排序数组中查找元素的第一个和最后一个位置
*/
// @lc code=start
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.empty())
return {-1, -1};
int l = 0, r = nums.size() - 1;
while (l < r){
long mid = l + (r - l) / 2;
if (nums[mid] >= target)
r = mid;
else
l = mid + 1;
}
int start = r;
if(nums[r]!=target)
return {-1, -1};
l = 0, r = nums.size() - 1;
while (l < r){
long mid = l + (r - l + 1) / 2;
if(nums[mid]<=target)
l = mid;
else
r = mid - 1;
}
int end = r;
return {start,end};
}
};
// @lc code=end
Leetcode69 x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
source code
/*
* @lc app=leetcode.cn id=69 lang=cpp
*
* [69] x 的平方根
*/
// @lc code=start
class Solution {
public:
int mySqrt(int x) {
long l = 0, r = x;
while(l<r){
long mid = l + (r - l + 1) / 2;
if (mid > x / mid)
r = mid - 1;
else
l = mid;
}
return l;
}
};
// @lc code=end
Leetcode278 第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例 1:
输入:n = 5, bad = 4
输出:4
解释:
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
示例 2:
输入:n = 1, bad = 1
输出:1
提示:
1 <= bad <= n <= 231 - 1
source code
/*
* @lc app=leetcode.cn id=278 lang=cpp
*
* [278] 第一个错误的版本
*/
// @lc code=start
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
long l = 1, r = n;
while(l<r){
long mid = l + (r - l) / 2;
if(isBadVersion(mid))
r = mid;
else
l = mid + 1;
}
return l;
}
};
// @lc code=end
Leetcode441 排列硬币
你总共有 n 枚硬币,并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯,其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。
给你一个数字 n ,计算并返回可形成 完整阶梯行 的总行数。
示例 1:
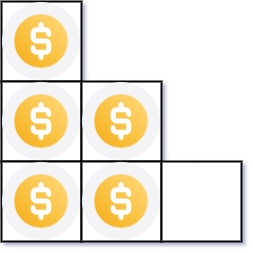
输入:n = 5
输出:2
解释:因为第三行不完整,所以返回 2 。
示例 2:
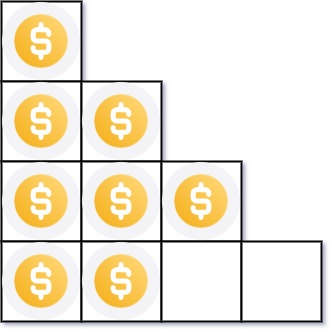
输入:n = 8
输出:3
解释:因为第四行不完整,所以返回 3 。
提示:
1 <= n <= 231 - 1
source code
/*
* @lc app=leetcode.cn id=441 lang=cpp
*
* [441] 排列硬币
*/
// @lc code=start
class Solution {
public:
int arrangeCoins(int n) {
int l = 1, r = n;
while(l<r){
long long mid = l + (r - l+1) / 2;
if ((long long)mid * (mid + 1) <= (long long)2 * n)
l = mid;
else
r = mid-1;
}
return l;
}
};
// @lc code=end
ACwing67 数字在排序数组中出现的次数
统计一个数字在排序数组中出现的次数。
例如输入排序数组 [1,2,3,3,3,3,4,5] 和数字 33,由于 33 在这个数组中出现了 44 次,因此输出 44。
数据范围
数组长度 [0,1000]
样例
输入:[1, 2, 3, 3, 3, 3, 4, 5] , 3
输出:4
source code
class Solution
{
public:
int getNumberOfK(vector<int> &nums, int k)
{
if (nums.empty())
return 0;
int l = 0, r = nums.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (nums[mid] >= k)
r = mid;
else
l = mid + 1;
}
if (nums[l] != k)
return 0;
int start = l;
l = 0, r = nums.size() - 1;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (nums[mid] <= k)
l = mid;
else
r = mid - 1;
}
int end = r;
if (start == end)
return end;
return start - end + 1;
}
};
Leetcode74 搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
- 每行中的整数从左到右按升序排列。
- 每行的第一个整数大于前一行的最后一个整数。
示例 1:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
示例 2:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
source code
/*
* @lc app=leetcode.cn id=74 lang=cpp
*
* [74] 搜索二维矩阵
*/
// @lc code=start
class Solution
{
public:
bool searchMatrix(vector<vector<int>> &matrix, int target)
{
int n = matrix.size(), m = matrix[0].size();
if (matrix.empty() || matrix[0].empty())
return 0;
vector<int> a;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
a.push_back(matrix[i][j]); //把二维matrix存到一维数组
int l = 0, r = a.size() - 1;
//二分
while (l < r)
{
int mid = l + r >> 1;
if (a[mid] >= target)
r = mid;
else
l = mid + 1;
}
if(a[r]!=target)
return 0;
return 1;
}
};
// @lc code=end
Leetcode162 寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
source code
class Solution
{
public:
int findPeakElement(vector<int> &nums)
{
int l = 0, r = nums.size() - 1;
whiel(l<r){
int mid = l + (r - l) / 2;
if(nums[mid] < nums[mid + 1])
l = mid + 1;
else
r = mid;
}
return r;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号