线段树历史信息问题的一类构建矩阵方法

前置知识：矩阵相关，线段树

本文记录一类历史信息问题的线段树解法，这个做法在比赛一题中为人所周知，现在，笔者希望在这里提出一种构造矩阵后能大大减少常数的维护方法。

最朴素的问题

考虑这样一个问题：区间加，区间最值，区间历史最值。

朴素的线段树维护会需要维护区间加/区间 \(\max\)/区间历史 \(\max\) 的 \(\text{tag}\)，其中有非常复杂的 \(\text{pushDown}\) 需要实现，但我们今天并不需要动脑子，只需要做一些体力劳动就好了。

考虑给序列每一个位置维护一个向量：

\[\begin{bmatrix} a & b \end{bmatrix} \]

其中 \(a\) 表示最大值， \(b\) 表示历史最大值。

\[\begin{bmatrix} a & b \end{bmatrix} \begin{bmatrix} v & v\\ -\infty & 0 \end{bmatrix} = \begin{bmatrix} a+v & \max\{a+v,b\} \end{bmatrix} \]

注意，这里的矩阵乘法是广义矩阵乘法，即 \((\max,+)\) 矩阵。

在这道题我们可能没有看出来维护矩阵的便利，再看下一道题会更加明显。

加上区间覆盖呢？

我们得到了 P4314，我们现在多了一个区间覆盖，怎么做？

之前维护标记的方法看起来有点复杂，矩阵这个时候就体现出了其优势，因为我们有区间覆盖，肯定是需要在向量中多加一个 \(0\) 来让我们对矩阵中的值本身取 \(\max\) 的。

\[\begin{bmatrix} a & b & 0 \end{bmatrix} \begin{bmatrix} -\infty & -\infty & -\infty\\ -\infty & 0 & -\infty\\ v & v & 0 \end{bmatrix} = \begin{bmatrix} v & \max\{v,b\} & 0 \end{bmatrix} \]

看起来我们有一个九倍常数的线段树，但实际上根本不是那么多，我们乘两个矩阵不难发现，有很多地方根本不会被更改，那么这些地方不论怎么乘都是常数，但是如何快速找到哪些地方是常数呢。

具体看看这个转移我们维护了什么，我们考虑这个矩阵有什么意义，一个元素在 \((x,y)\) 位置表示在向量中第 \(x\) 项对于第 \(y\) 项有一定贡献。

我们把这个转移关系的图画出来，如果这一位是 \(-\infty\)，对于 \((\max,+)\) 矩阵，代表不可能做出贡献，我们就不连边。

我们把这两个矩阵一起构成的图画出来看看：

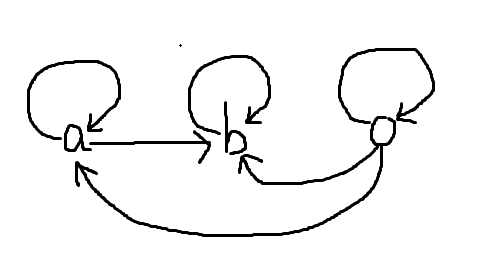
大概是这个样子，我们考虑一个矩阵中的值需要被维护，当且仅当它们之间有直接或者间接的到达关系。

但是有一些自环同样没有用，就比如 \(0\) 本身的自环，无论如何取值都是 \(0\)，所以它也是一个常量，没有维护的价值。

为什么这个做是对的

我们把这个矩阵看成一个邻接矩阵，画出来的图就是上面那样，考虑矩阵乘法对于邻接矩阵意味着 Floyd，也就是说，我们多次矩阵乘法会出现有意义价值的那些数，本质上是对一个图做了传递闭包。

也就是说，我们可以把它看成向量中元素互相贡献的有向图，我们看这个图哪些点之间可以到达就去维护哪些点，具体转移就是类似一个 \(i\rightarrow j\rightarrow k\) 的过程。

比赛

一句话题意，让我们求如下式子的值：

\[\sum^r_{i=l} \sum^r_{j=i} (\max^j_{k=i}A_k)(\max^j_{k=i}B_k) \]

现在我们从区间历史最值到区间历史和，只要把广义矩阵乘法换成真正的矩阵乘法就好了。

为了维持这个矩阵，我们考虑到这种和的问题都要同时维护区间长度，同时，我们要维护两个数组和，两个数组乘积和，区间历史乘积和。

\[\begin{bmatrix} a & b & ab & c & len \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 & 0 & 0\\ 0 & 1 & v & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ v & 0 & 0 & 0 & 1\\ \end{bmatrix} = \begin{bmatrix} v & b & vb & c & len \end{bmatrix} \]

\[\begin{bmatrix} a & b & ab & c & len \end{bmatrix} \begin{bmatrix} 1 & 0 & v & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & v & 0 & 0 & 1\\ \end{bmatrix} = \begin{bmatrix} a & v & av & c & len \end{bmatrix} \]

\[\begin{bmatrix} a & b & ab & c & len \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{bmatrix} = \begin{bmatrix} a & b & ab & c+ab & len \end{bmatrix} \]

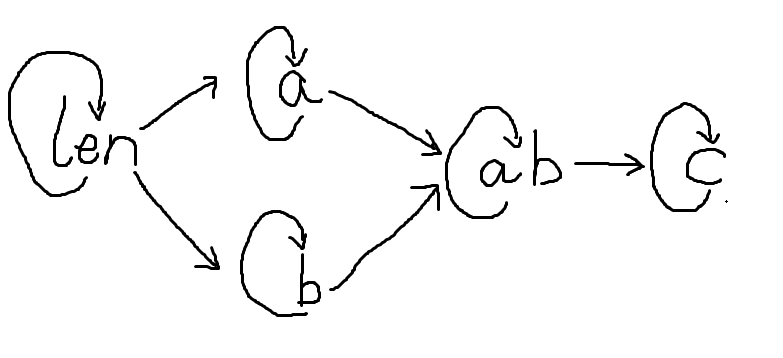
注意到我们只有 \(14\) 个可用转移，而且有一些完全没有用的，比如 \(\text{len}\) 和 \(\text{ab}\) 对自己的转移恒为 \(1\)。

于是我们只剩 \(12\) 个可用转移，建个图跑一下就找到了所有的转移应当为什么样子（类似 Floyd ）。

转移如下：

ans.x11=x11*ano.x11;
ans.x13=x11*ano.x13+x13*ano.x33;
ans.x14=x11*ano.x14+x13*ano.x34+x14;
ans.x22=x22*ano.x22;
ans.x23=x22*ano.x23+x23*ano.x33;
ans.x24=x22*ano.x24+x23*ano.x34+x24;
ans.x33=x33*ano.x33;
ans.x34=x33*ano.x34+x34;
ans.x51=x51*ano.x11+ano.x51;
ans.x52=x52*ano.x22+ano.x52;
ans.x53=x51*ano.x13+x52*ano.x23+x53*ano.x33+ano.x53;
ans.x54=x51*ano.x14+x52*ano.x24+x53*ano.x34+x54+ano.x54;

其中 \(\text{ano}\) 为右乘的矩阵，\(\text{ans}\) 为乘积。