20241224北京总结

模拟赛

\(T1\) , 连图的方案数计数 , 显然是 \(Prufer\) 序列个数 , 大力推式子 , 之后做一个背包

我考场上没想到 \(Pruffer\) 序列 , 也没推明白式子 , 一方面经验问题 , 另一方面王铎讲完的东西没能完全理解 , 痛失 \(n^3\) 这个分

后面多项式优化/生成函数不会到无所谓 , 有点神秘了疑似

\(T2\) , 是一眼 \(dp\) , \(40pts\) 可做 , 场上就奔着这个分做的

考虑三维状态 , 但有个 \(side\) 被我想假了 , 又是 \(subtask\) 所以挂 \(0\) 了

正解就是我的 \(dp\) 上加优化 , 我其实看出来了 , 就是转移点都是一些 \(i=j\) , \(i=k\) 的点 , 首先就能差掉一维 , 找到一个 \(n^2\) 做法 , 然后 \(n\) 滚掉又差一维 , 然后在上面上线段树转移 , 总复杂度 \(nlogn\)

\(T3\) , 打个表出来找规律 , 发现这个 \(p\) 是一些 \(q\) 加权求和 , 二分求出应该到哪个 \(q\)

正解不会 , 疑似有点神秘了 , 拉差这些数学还是疑似有点太太不会了

接下来是晚上学了一些自动机 , 为明天的字符串做准备

自动机

我感性理解一下 , 可能不太严格

自动机就是一个把类似序列一样的东西做成判定性的问题 , 并给出这个判定性的问题一个答案

举个例子 , 给你一个串 , 判定它是否为一个含有 \(001\) 的串的自动机如下

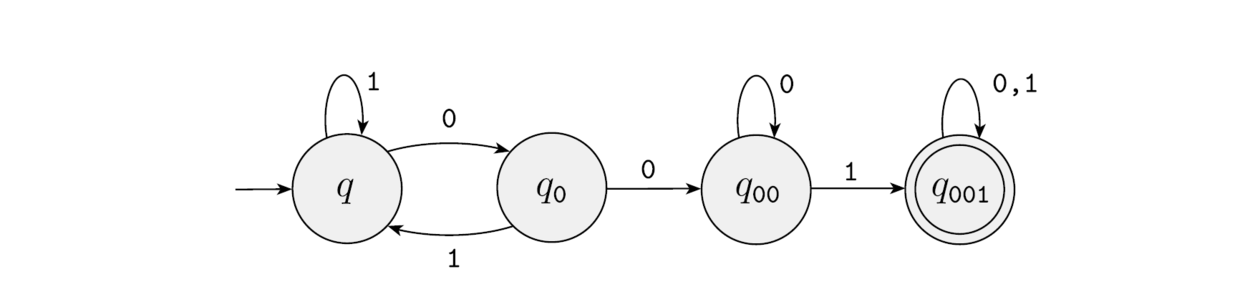
可以看到 , 这个自动机构成了一个类似于有向图的东西 , 前面箭头指的 \(q\) 即为这个自动机的起始状态 , 画圈的为接受状态集合 , 即如果你最后走到了这个状态 , 你的结果就被判定为 \(T\)

那么连边是什么呢 ? 就是转移函数 , 举个例子 , \(f(q,0)=q_0\) , \(f(q_{001},1)=q_{001}\) , 第一个参数和返回值都是状态 , 第二个参数是字符集中得字符 , 在上图中表现为边权

如何判定一个串是否课接受 , 如果最后没走到可接受的状态集合 , 或者是中间走出了一些未定义的转移 ( 之后只能从未定义转向未定义 , 某种意义上也没走到可接受 ) , 就不算是判定为 \(T\)

了解什么是自动机以后 , 不妨来看看之前学的一些字符串算法是否是自动机

\(Trie\) 树 , 典型的自动机 , \(Trie\) 树上的边就是一个转移 , 在字符串集合中转移

\(kmp\) , 自动机 , 意为接受以 \(s\) 为后缀的的字符串

\(AC\) 自动机 , 就是接受以 \(s\) 为后缀的字符串同时在字符串集合中转移 , 所以他其实是 \(Trie\) 树和 \(kmp\) 在自动机意义下的组合

所以以上算法都可以解决一类判定上的问题 , 这就是自动机的作用

其实还学了 \(PAM\) , 但是没写代码 , 就明天在说