栈的应用----中缀表达式转后缀表达式的算法

前提

一个中缀表达式可以对应多个后缀表达式，机器算法得出的是性质最好的左优先的后缀表示式。

 

算法核心思想

1、一切过程皆是数据。

2、一个中缀表达式的操作数，左右两边都各有一个符号，这个数要么先参与左边的符号运算，要么先参与右边的符号运算，具体视优先级情况而定。

 

3、中缀表达式的界定符，即括号，规定了最高的优先级，相当于在括号内先递归调用一次无括号算法，然后再将返回的数字参与到无括号算法当中，相当于是一次无括号转换算法的递归调用。

 

三种情况

 

 

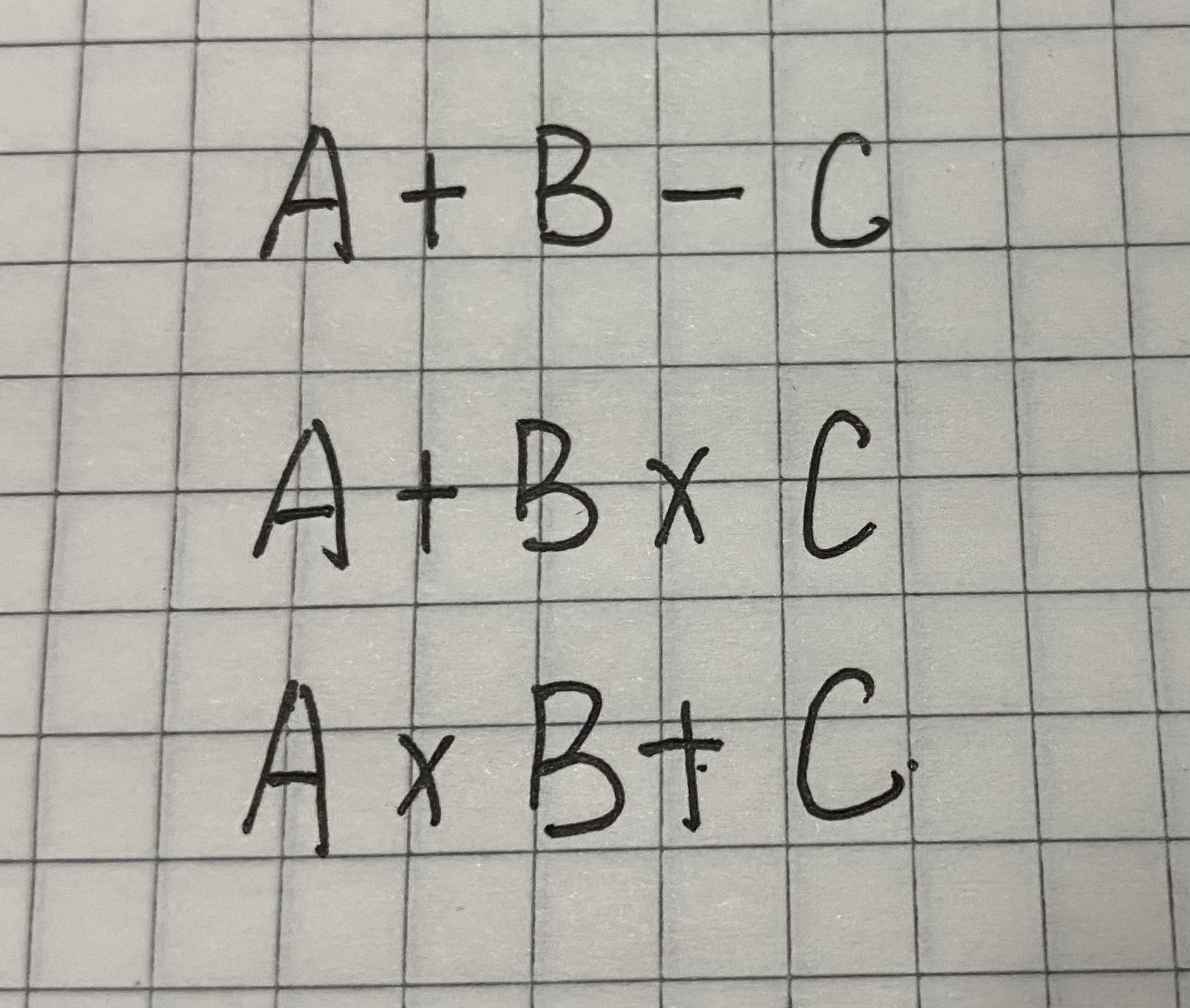
注意 ，这里的ABC既可以指一个操作数，也可以指一个多操作数和多运算符构成的式子，每次经过一次运算后就把运算元素看成一个整体，最终就会简化为只有三种情况

1、优先级相同，先输出哪个都行，但是由于左优先原则先输出左边的

2、优先级前小后大，不弹栈，因为后面的优先级更高需要先执行，需要压栈

3、优先级前大后小，必须弹栈，因为要让优先级高的运算符先执行

4、括号相当于一次递归调用

算法具体流程

1、遇到操作数。直接加入后缀表达式（因为后缀表达式和中缀表达式的操作数顺序一样）

2、遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符（），如果遇到（或栈空则停止。之后再把当前运算符入栈。

3、遇到界限符。遇到（直接入栈，遇到）则依次弹出栈内运算符并加入后缀表达式，直到弹出（为止。（（不加入后缀表达式）