N 皇后-力扣解题

n 皇后问题 研究的是如何将 n 个皇后放置在 n*n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

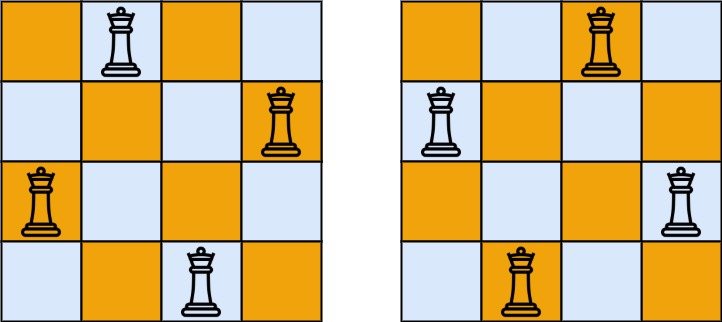
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

n, *_ = map(int, input().split())

table = [['.']* n for _ in range(n)]
# 记录皇后以存在的列数
cols= []
def solveNQueens(n):
    # 存答案的列表
    res = []
    for col in range(n):
        table[0][col] = 'Q'
        cols.append(col)
        # 重第一行的位置开始尝试添加皇后，后面就往下面进行搜索
        dfs(table, 1, 0, res)
            # 搜完成后进行回溯
        table[0][col] = '.'
        cols.remove(col)
    return res

import copy
def dfs(table, x, y, res) -> None:
    if y == n:
        return
    if x == n:
        res.append(copy.deepcopy(table))
        return

    if y not in cols:
        if check(table,x, y):
            table[x][y] = 'Q'
            cols.append(y)
            dfs(table, x+1, 0, res)
            table[x][y] = '.'
            cols.remove(y)
    dfs(table, x, y+1, res)


def check(table, row, col):
    for i in range(len(table)):
        for j in range(len(table[0])):
            if i+j == row+col or i-j == row-col:
                if table[i][j] == 'Q':
                    return False
    return True


def parse(a):
    res = []
    for i in range(len(a)):
        b = []
        for j in range(len(a[i])):
            s = ''
            for k in a[i][j]:
                if k == '.':
                    s+='.'
                if k == 'Q':
                    s+= 'Q'
            b.append(s)
        res.append(b)
    return res

print(parse(solveNQueens(n)))