UVA 部分刷题记录
UVA10780 Again Prime? No Time. 打表找规律 思维
题意:求
题解:数学,题解见:http://blog.cinema000.xyz/

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int M = 10005;
int tot, ans, cnt[M], yz[M];
void init(){
tot = 0;
ans = 1e9 + 7;
}
bool isprime(int x){
for(int i = 2; i * i <= x; i++)
if(x % i == 0)return 0;
return 1;
}
void divide(int x){
for(int i = 2; i * i <= x; i++)
if(x % i == 0){
yz[++tot] = i; cnt[tot] = 0;
while(x % i == 0) x /= i, cnt[tot]++;
}
if(x != 1)yz[++tot] = x, cnt[tot] = 1;
}
int get(int x, int n){
int k = 0, now = 1, ret = 0;
while(1){
now *= x, k++;
int d = n / now;
if(!d)break;
ret += d;
}
return ret;
}
int main(){
int T, idc = 0, m, n;
scanf("%d", &T);
while(T--){
init();
scanf("%d%d", &m, &n);
printf("Case %d:\n", ++idc);
if(isprime(m)){
int ans = get(m, n);
ans ? printf("%d\n", ans) : puts("Impossible to divide");
}
else {
divide(m);
for(int i = 1; i <= tot; i++)
ans = min(ans, get(yz[i], n) / cnt[i]);
ans ? printf("%d\n", ans) : puts("Impossible to divide");
}
}
}
UVA10859 Placing Lampposts 有借鉴价值的建模 思维
给定一个n个点m条边的无向无环图,在尽量少的节点上放灯,使得所有边都与灯相邻(被灯照亮)。
在灯的总数最小的前提下,被两盏灯同时照亮的边数应该尽可能大。
题解:这道题转化为 在灯的总数最小的前提下,被一盏灯照亮的边数应该尽可能小, 就成了一个经典模型;
化为求 z = M * x + y; M是一个极大的数, 使的y的影响在x下面就没有用了;x为灯的总数, y为被一盏灯照亮的边数, 用上司的舞会做一个函数最大值;

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int M = 1005, mod = 5000;
int h[M], dp[M][2], tot; bool vis[M];
struct edge{int nxt, v;}G[M << 1];
void add(int u, int v){
G[++tot].v = v; G[tot].nxt = h[u]; h[u] = tot;
}
void init(){
memset(h, 0, sizeof(h));
tot = 0;
memset(vis, 0, sizeof(vis));
}
void dfs(int u, int f){
vis[u] = 1;
int tmp1 = 0, tmp2 = 0;
for(int i = h[u]; i; i = G[i].nxt){
int v = G[i].v;
if(v == f)continue;
dfs(v, u);
tmp1 += dp[v][1] + 1;
tmp2 += min(dp[v][1], dp[v][0] + 1);
}
dp[u][0] = tmp1;
dp[u][1] = mod + tmp2;
}
int main(){
int T;
scanf("%d", &T);
while(T--){
init();
int n, m, u, v, ans = 0;
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
scanf("%d%d", &u, &v);
u++, v++;
add(u, v), add(v, u);
}
for(int i = 1; i <= n; i++)
if(!vis[i]){
dfs(i, i);
ans += min(dp[i][0], dp[i][1]);
}
printf("%d %d %d\n",ans / mod, m - ans % mod, ans % mod);
}
}
UVA11134 Fabled Rooks 分开考虑+贪心 思维
在一个n*n(1<=n<=5000)的棋盘上放置n个车,每个车都只能在给定的一个矩形(xli,xri,yli,yri)里放置,使其n个车两两不在同一行和同一列,判断并给出解决方案。
题解:x,y互不影响,x,y分别做一次类似区间覆盖的贪心,如果x,y都合法,那么这个点的唯一位置就可以确定了;

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int M = 5005;
int tox[M], toy[M];
struct Node{int id, xl, yl, xr, yr;}p[M];
bool cmp1(Node A, Node B){return A.xl == B.xl ? A.xr < B.xr : A.xl < B.xl;}
bool cmp2(Node A, Node B){return A.yl == B.yl ? A.yr < B.yr : A.yl < B.yl;}
int main()
{
//puts("INPUT:");
int n, idc = 0;
while(scanf("%d", &n) == 1 && n){
int xl, yl, xr, yr;
for(int i = 1; i <= n; i++){
scanf("%d%d%d%d", &xl, &yl, &xr, &yr);
p[i] = (Node){i, xl, yl, xr, yr};
}
bool fg = 1;
memset(tox, 0, sizeof(tox));
memset(toy, 0, sizeof(toy));
sort(p + 1, p + 1 + n, cmp1);
for(int i = 1, t = 0; i <= n && t <= n; i++){
while((++t) <= n)
if(i >= p[t].xl && i <= p[t].xr){
tox[p[t].id] = i; break;
}
for(int x = t + 1; x <= n; x++) {
if(p[x].xl > i)break;
p[x].xl = i + 1;
}
if(t < n) sort(p + t + 1, p + n + 1, cmp1);
}
for(int i = 1; i <= n; i++)fg &= (tox[i] != 0);
if(!fg){puts("IMPOSSIBLE");continue;}
sort(p + 1, p + 1 + n, cmp2);
for(int i = 1, t = 0; i <= n && t <= n; i++){
while((++t) <= n)
if(i >= p[t].yl && i <= p[t].yr){
toy[p[t].id] = i; break;
}
for(int x = t + 1; x <= n; x++) {
if(p[x].yl > i)break;
p[x].yl = i + 1;
}
if(t < n)sort(p + t + 1, p + n + 1, cmp2);
}//for(int i = 1; i <= n; i++)printf("%d ", toy[i]);
for(int i = 1; i <= n; i++)fg &= (toy[i] != 0);
if(!fg){puts("IMPOSSIBLE");continue;}
for(int i = 1; i <= n; i++)printf("%d %d\n", tox[i], toy[i]);
}
return 0;
}
UVA10795 A Different Task 经典递归思路 思维
题意:给出汉诺塔的初末状态,问最少多少步可以移到目标状态;
题解:首先大的并且已经在目标位置上的肯定不会移动,我们就只需要将k-1根移动到过度柱子 + 最后把k-1根从过度柱子移到目标状态 + 1;
这个用一个dfs(now, k, final)实现,还是先把k - 1移到过度柱子,此时过度柱子上的一定是从小到大,我们再把这k-1根移到final上,这个时候相当于普通的汉诺塔;步数是2^(k-1) + 1(移动一根k的步数);

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int pos[80], tgr[80];
#define ll long long
ll dfs(int * P, int k, int goal){
if(!k) return 0;
if(P[k] == goal) return dfs(P, k - 1, goal);
return dfs(P, k - 1, 6 - P[k] - goal) + (1LL << (k - 1));
}
int main()
{
int n, idc = 0;
while(scanf("%d", &n) == 1 && n){
ll ans = 0;
for(int i = 1; i <= n; i++)scanf("%d", &pos[i]);
for(int i = 1; i <= n; i++)scanf("%d", &tgr[i]);
for(int i = n; i; i--){
if(pos[i] != tgr[i]){
ans = dfs(pos, i - 1, 6 - pos[i] - tgr[i]) + dfs(tgr, i - 1, 6 - pos[i] - tgr[i]) + 1;
break;
}
}
printf("Case %d: %lld\n", ++idc, ans);
}
return 0;
}
UVA1326 Jurassic Remains 双向搜索模板+二进制枚举 代码
题意:相当于给n个01串,选尽量多的串使他们的抑或和为0;n <= 25;
题解:双向搜索,先搜出前面抑或得到的子串,在搜后面得到的子串,比较相同;

#include<bits/stdc++.h>
using namespace std;
const int M = 30;
int a[M];
map <int, int> table;
inline int bitcount(int x){
if(!x) return 0;
return bitcount(x >> 1) + (x&1);
}
char c[1005];
int main(){
int n;
while(scanf("%d", &n) == 1){
for(int i = 1; i <= n; i++){
scanf("%s", c);
a[i] = 0;
int len = strlen(c);
for(int j = 0; j < len; j++) a[i] ^= ( 1 << (c[j] - 'A') );
}
table.clear();
int ans = 0;
int n1 = n/2, n2 = n - n1;
for(int s = 0; s < (1 << n1); s++){
int x = 0;
for(int i = 1; i <= n; i++)
if((1 << (i-1)) & s) x ^= a[i];
if(!table.count(x) || bitcount(s) > bitcount(table[x])) table[x] = s;
}
for(int s = 0; s < (1 << n2); s++){
int x = 0;
for(int i = n1 + 1; i <= n; i++)
if((1 << (i-n1-1)) & s) x ^= a[i];
if(table.count(x) && bitcount(s) + bitcount(table[x]) > bitcount(ans)){
ans = table[x] + (s << n1);
// printf("%d %d %d %d\n", x, table[x], s, ans);
}
}
printf("%d\n", bitcount(ans));
if(ans){
for(int i = 1; i <= n; i++)
if((1 << (i - 1)) & ans)printf("%d ", i);
}
puts("");
}
}
UVA1467 Installations 贪心推理题 思维
题意,n(<=500)个工作,有持续时间和限制时间,每个工作惩罚时间= max(0, now - limit),安排工作顺序,使最大的两个惩罚值之和最小,求最小值;
题解:先按照结束时间为第一关键字,持续时间为第二关键字排序,这样可以保证最大的惩罚值最小,在此基础上第二大的最小;但是有可以最大的变大,第二大变小更优;
找到两个最大值的位置,p1, p2(p1 < p2);枚举p2之前的每个位置,把他放在p2后面,更新最大,第二大值,证明见https://blog.csdn.net/corncsd/article/details/18948953

#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <cmath> #include <ctime> using namespace std; const int M = 505; int ta, tb, n, mx1, mx2, p; struct Job{ int s, t; }a[M]; bool cmp(Job A, Job B){ return A.t == B.t ? A.s < B.s : A.t < B.t; } int wrk(int x){ ta = tb = 0; int now = 0; for(int i = 1; i <= p; i++){ if(i == x)continue; now += a[i].s; int tp = max(0, now - a[i].t); if(tp > ta)tb = ta, ta = tp, mx2 = mx1, mx1 = i; else if(tp > tb)tb = tp, mx2 = i; } now += a[x].s; int tp = max(0, now - a[x].t); if(tp > ta)tb = ta, ta = tp, mx1 = x; else if(tp > tb)tb = tp, mx2 = x; return ta + tb; } int main(){ int T; scanf("%d", &T); while(T--){ scanf("%d", &n); p = n; for(int i = 1; i <= n; i++)scanf("%d%d", &a[i].s, &a[i].t); sort(a + 1, a + 1 + n, cmp); a[0].t = 1e9; int ans = wrk(0); p = max(mx1, mx2); for(int i = 1; i <= p; i++) ans = min(ans, wrk(i)); printf("%d\n", ans); } }
UVA1335 Beijing Guards 贪心推理 思维
题意:n(<=100000)个人站成一圈,每个人要a个礼物,相邻两人礼物编号不可重复,每个编号有礼物无限个,求最小编号可以是多少;
题解:若n为偶数,答案是max(a[i] + a[i+1]),规律好找;若n为奇数,我们就尽量让为偶数的人选编号小的礼物,奇数人选编号大的,这样可以避免冲突;编号就二分好了;

#include<bits/stdc++.h>
using namespace std;
const int M = 100000 + 5;
int n, lft[M], rigt[M], a[M];
bool check(int k){
lft[1] = a[1]; rigt[1] = 0;
int y = k - a[1];
for(int i = 2; i <= n; i++){
if(i%2){
rigt[i] = min(a[i], y - rigt[i - 1]);
lft[i] = a[i] - rigt[i];
}
else{
lft[i] = min(a[i], a[1] - lft[i - 1]);
rigt[i] = a[i] - lft[i];
}
}
return lft[n] == 0;
}
int main(){
// freopen("c.in","r",stdin);
// freopen("my.out","w",stdout);
//cout<<bitcount(6)<<endl;
while(scanf("%d", &n) == 1 &&n){
int ans = 0, L = 0, R = 0;
for(int i = 1; i <= n; i++)scanf("%d", &a[i]);
a[n + 1] = a[1];
for(int i = 1; i <= n; i++)
L = max(L, a[i] + a[i + 1]), R = max(R, a[i] * 3);
if(n == 1)ans = a[1];
else if(n%2){
int lf = L, rg = R;
while(lf <= rg){
int mid = (lf + rg) >> 1;
if(check(mid))rg = mid - 1, ans = mid;
else lf = mid + 1;
}
}
else ans = L;
printf("%d\n", ans);
}
}
我在n=1是直接return a[1], 搞了半天,多组数据呵呵
UVA1099 Sharing Chocolate 好题 思维+代码
题意:x*y大小的巧克力,问最后能否切成x1*y1,x2*y2,x3*y3……xn*yn (n <= 15)的巧克力;
题解:虽然n很小,但是想搜索很难啊;状压DP, dp[s][x][y] 表示选择集合为s的块,能否凑出x*y;然后可以把max(x, y)压掉,用总面积表示,细节看代码;

#include<bits/stdc++.h>
using namespace std;
const int M = (1 << 15) + 1;
int dp[M][105], sum[M], a[16];
inline int bitcount(int x){return x == 0 ? 0 : bitcount(x >> 1) + (x & 1);}
bool dfs(int r, int res){
if(dp[res][r] != -1) return dp[res][r];
if(bitcount(res) == 1) return dp[res][r] = 1;
int y = sum[res]/r;
for(int s0 = res&(res-1); s0; s0 = res&(s0-1)){
int s1 = res - s0;
if((sum[s0]%r == 0 && dfs(min(r, sum[s0]/r), s0)) && dfs(min(r, sum[s1]/r), s1))
return dp[res][r] = 1;
if((sum[s0]%y == 0 && dfs(min(y, sum[s0]/y), s0)) && dfs(min(y, sum[s1]/y), s1))
return dp[res][r] = 1;
}
return dp[res][r] = 0;
}
int main(){
int n, X, Y, idc = 0;
//cout<<bitcount(6)<<endl;
while(scanf("%d", &n)&&n){
memset(sum, 0, sizeof(sum));
memset(dp, -1, sizeof(dp));
scanf("%d%d", &X, &Y);
for(int i = 1; i <= n; i++)scanf("%d", &a[i]);
for(int s = 1; s < (1 << n); s++)
for(int i = 1; i <= n; i++)
if(s & (1 << (i - 1))) sum[s] += a[i];
int All = (1 << n) - 1;
if(sum[All] % X || sum[All] != X*Y){
printf("Case %d: No\n", ++idc);continue;
}
bool ans = dfs(min(X, Y), All);
printf("Case %d: ",++idc);
ans == 1 ? puts("Yes") : puts("No");
}
}
UVA11090 Going in Cycle!! SPFA跑负环 思维
给定一个N个点M条边的带权有向图,求平均值最小的回路
N<=50
题解:我们要求平均权值最小,所以考虑二分答案。
当它小于mid的时候,这就意味着: a_1+a_2+......+a_k<k*mid
即:(a_1-mid)+(a_2-mid)+......(a_k-mid)<0
这时我们发现只要我们开始的时候将各个边处理一下,之后需要的操作就是判负环了.......
(我写二分时,用ans记录合法的L,R,但有一组因为精度原因,一来就L==R,而ans初值为1,我因为这个原因wa了一页)

# include <bits/stdc++.h>
const double eps = 1e-8 , dnf = 5e13 + 7 ;
const int N = 10000 + 5 ;
int head [ N ] , nxt [ N << 1 ] , to [ N << 1 ] , cn ;
int num [ N ] , x , y ;
double dis [ N ] , w [ N ] , z ;
int n , m , T ;
bool vis [ N ] ;
std :: queue < int > q ;
void create ( int u , int v , double d ) {
cn ++ ;
w [ cn ] = d ;
to [ cn ] = v ;
nxt [ cn ] = head [ u ] ;
head [ u ] = cn ;
}
bool spfa ( int s , double l ) {
memset ( vis , false , sizeof ( vis ) ) ;
for ( int i = 1 ; i <= n ; i ++ )
dis [ i ] = dnf ;
memset ( num , 0 , sizeof ( num ) ) ;
q . push ( s ) ;
dis [ s ] = 0 ;
while ( ! q . empty ( ) ) {
int u = q . front ( ) ; q . pop ( ) ; vis [ u ] = false ;
for ( int i = head [ u ] ; i ; i = nxt [ i ] ) {
int v = to [ i ] ;
if ( dis [ v ] > dis [ u ] + w [ i ] - l ) {
dis [ v ] = dis [ u ] + w [ i ] - l ;
if ( ! vis [ v ] ) {
num [ v ] ++ ;
if ( num [ v ] > n ) return true ;
vis [ v ] = true ;
q . push ( v ) ;
}
}
}
}
return false ;
}
bool check ( double lim ) {
for ( int i = 1 ; i <= n ; i ++ )
if ( spfa ( i , lim ) )
return true ;
return false ;
}
double divx ( double l , double r ) {
double ans = - 1 ;
while ( l <= r - eps ) {
double mid = ( r + l ) / 2 ;
if ( check ( mid ) )
r = mid - eps , ans = mid ;
else
l = mid + eps;
}
return ans ;
}
void init ( ) {
cn = 0 ;
memset ( head , 0 , sizeof ( head ) ) ;
}
/*
1
1 1
1 1 3.5
*/
int main ( ) {
int kase = 0 ;
scanf ( "%d" , & T ) ;
while ( T -- ) {
kase ++ ;
init ( ) ;
scanf ( "%d%d" , & n , & m ) ;
for ( int i = 1 ; i <= m ; i ++ )
scanf ( "%d%d%lf" , & x , & y , & z ) , create ( x , y , z ) ;
double ansx = divx ( 0 , 1e8 ) ;
if ( ansx == - 1 ) printf ( "Case #%d: No cycle found.\n" , kase ) ;
else printf ( "Case #%d: %.2lf\n" , kase , ansx ) ;
}
return 0 ;
}
UVA11374 Airport Express dijstra 思维+代码
题意:
在IokhIokh市中,机场快线是市民从市内去机场的首选交通工具。机场快线分为经济线和商业线两种,线路、速度和价钱都不同。你有一张商业线车票,可以坐一站商业线,而其他时候只能乘坐经济线。假设换乘时间忽略不计,你的任务是找一条去机场最快的线路。
输入格式:
输入包含多组数据。每组数据第一行为33个整数N, ,S和E(2≤N≤500,1≤S,E≤100),即机场快线中的车站总数,起点和终点(即机场所在站)编号。下一行包含一个整数M(1≤M≤1000),即经济线的路段条数。以下M行每行3个整数X, Y, Z,K(1≤K≤1000),以下KK行是这些路段的描述,格式同经济线。所有路段都是双向的,但有可能必须使用商业车票才能到达机场。保证最优解唯一。
输出格式:
对于每组数据,输出3行。第一行按访问顺序给出经过的各个车站(包括起点和终点),第二行是换乘商业线的车站编号(如果没有商业线车票,输出Ticket Not Used),第三行是总时间。
题解:


#include <cstdio> #include <cstring> #include <queue> using namespace std; const int N = 505; const int M = 5005; const int INF = 0x3f3f3f3f; typedef long long ll; int n, s, t; int vis[N], d[2][N], en; int head[M]; int pre[2][N]; struct node { int to, dis, next; }edge[N * M]; void init(); void addEdge(int u,int v,int x) { edge[en].to = v; edge[en].next = head[u]; edge[en].dis = x; head[u] = en++; edge[en].to = u; edge[en].next = head[v]; edge[en].dis = x; head[v] = en++; } void SPFA(int flag) { queue<int> Q; for(int i = 1; i <= n; i++) { d[flag][i] = INF; vis[i] = 0; pre[flag][i] = -1; } d[flag][s] = 0; vis[s] = 1; pre[flag][s] = s; Q.push(s); while(!Q.empty()) { int u = Q.front(); vis[u] = 0; Q.pop(); for(int i = head[u]; i != -1; i = edge[i].next) { int v = edge[i].to; //.fprintf(stderr, "%d ", v); if(d[flag][u] + edge[i].dis < d[flag][v]) { d[flag][v] = d[flag][u] + edge[i].dis; pre[flag][v] = u; if(!vis[v]) { Q.push(v); vis[v] = 1; } } } } } void input() { int num, a, b, c; scanf("%d", &num); for (int i = 0; i < num; i++) { scanf("%d %d %d", &a, &b, &c); addEdge(a, b, c); } } void print(int x) { if (pre[0][x] == x) { printf("%d", x); return; } print(pre[0][x]); printf(" %d", x); } void solve() { int num, a, b, c; int Min = d[0][s], tU = -1, tV = -1; scanf("%d", &num); for (int i = 0; i < num; i++) { scanf("%d %d %d", &a, &b, &c); if (d[0][a] + d[1][b] + c < Min) { Min = d[0][a] + d[1][b] + c; tU = a, tV = b; } if (d[0][b] + d[1][a] + c < Min) { Min = d[0][b] + d[1][a] + c; tU = b, tV = a; } } if (tU == -1) { print(s); puts(""); printf("Ticket Not Used\n"); } else { print(tU); for (int i = tV; i != s; i = pre[1][i]) printf(" %d", i); printf(" %d\n", s); printf("%d\n", tU); } printf("%d\n", Min); } int main() { // freopen("c.in","r",stdin); // freopen("std.out","w",stdout); int Case = 1; while (scanf("%d %d %d", &n, &s ,&t) == 3) { memset(head, -1, sizeof(head));en = 0; if (Case != 1) puts(""); Case++; input(); SPFA(0); s = t; SPFA(1); solve(); } return 0; }
UVA10825 Anagram and Multiplication 思维
题目大意:给出m和n,要求你求出一个m位的n进制数,这个数分别乘上1,2,..,m之后的值是这个数每位上的数的排列组合中的其中一种,求这个数
解题思路:这题的难点是怎么枚举这个数。因为要分别乘上1,2,..,m,如果我们枚举这个数的最后一位的话,乘上这些数后不然得出最后一位的值,而这些值必然是属于这个数的,只是不知道再那个位置上而已,所以要对这些数进行排列组合,然后再进行确认,确认的过程就是暴力的过程

#include<bits/stdc++.h>
using namespace std;
int n, m;
int arr[10];
bool vis[10];
#define RG register
int main(){
//freopen("c.in","r",stdin);
//freopen("c.out","w",stdout);
while(scanf("%d%d", &m, &n) == 2){
if(!n&&!m)break;
int ok=0;
for(int i = 1; i < n; i++){
arr[1] = i;
for(int j = 2; j <= m; j++) arr[j] = i * j % n;
//for(int j = 1; j <= m; j++) printf("%d", arr[j]);puts("");
sort(arr + 1, arr + 1 + m);
do{
int fg = 0;
for(RG int p = 2; p <= m; p++){
memset(vis, 0, sizeof(vis));
int tot = 0, c = 0;
fg = 0;
for(RG int j = 1; j <= m; j++){
int now = (arr[j] * p + c) % n;
c = (arr[j] * p + c) / n;
//if(check())printf("%d %d %d ", arr[j], now, c);
for(RG int k = 1; k <= m; k++)
if(!vis[k] && now == arr[k]){vis[k] = 1; tot++; break;}
}
/*if(check()){
printf("\n%d: ", p);
for(int j=1;j<=m;j++) if(vis[j])printf("%d ", arr[j]);
printf("FUCK THAT%d\n", tot);
}*/
if(tot != m || !arr[m]){fg = 1; break;}
}
if(!fg){
for(int j = m; j>1; j--){
printf("%d ", arr[j]);
}
printf("%d\n",arr[1]);
ok = 1;
break;
}
}while(next_permutation(arr + 1, arr + 1 + m));
if(ok)break;
}
if(!ok)printf("Not found.\n");
}
}
UVA11538 Chess Queen 数学+思维
题目大意:给定一个棋盘,在棋盘上放两个皇后(一白一黑),求使得两个皇后相互攻击(在一行、一列或对角线)的方案数。
解题思路:
1、我们首先可以想到的是一个皇后在一个任意的位置,另一个皇后可以放的在同一行或在同一列的方案数有(m-1+n-1),棋盘上一共有m*n个格子,所以可放在同行或同列相互攻击的方案是ans=(m-1+n-1)*m*n;
2、同行同列的方案数已经算出来了,现在我们计算对角线上的方案数吧,因为左斜和右斜的方案是一样多的,所以我们只要求出左斜线即可知道右斜线的方案数。
3、左斜线,首先我们要考虑到的是:斜线的最大值,即为min(m,n),那我们就把x=max(m,n)看作行,y=min(m,n)看作列,所以我们的2~y-1行每行的格子数就是行号数,大于等于y的行号数都只有y个格子,所以等于Y个格子的左斜线有(y-x+1)——每一条上可以任选两个点放置皇后,即cnt+=i*(i-1)*2; cnt+=(n-m+1)*m*(m-1);
4、即总方案数:ans+2*cnt;

#include <iostream> #include <cstring> #include <cstdio> #include <algorithm> using namespace std; #define ll unsigned long long int main(){ ll n, m; while(cin>>n>>m ){ if(!n&&!m)break; if(n > m) swap(n, m); ll ans = m*(m-1)*n + n*(n-1)*m; ans -= n*(n-1)*2; ans += 2*(n-1)*n*(2*n - 1)/3; ans += (m-n+1)*(n-1)*n*2; //printf("Case %d: %lld\n", ++idc, ans); cout<<ans<<endl; } }
UVA11806 Cheerleaders 容斥原理+二进制 数学+思维+代码
题意:在一个m*n的矩形网格里放k个相同的石子,问有多少种方法?每个格子最多放一个石子,所有石子都要放完,并且第一行、最后一行、第一列、最后一列都得有石子。
思路:假设满足第一行没有石子的方案集为A,最后一行没有石子的方案集为B,第一列没有石子的方案集为C,最后一列没有石子的方案集为D,全集为S,则所求答案就是“在S中但不在A,B,C,D任何一个集合中”的元素个数,这里就是运用容斥原理。程序中可以用二进制来表示集合。

#include <cstdio>
#include <cstdlib>
#include <ctime>
int C[505][505];
const int mod = 1000007;
inline int moc(int a){return a >= mod ? a - mod : a;}
void init(){
for(int i = 0; i <= 500; i++)
for(int j = 0; j <= i; j++)
if(i == j || j == 0) C[i][j] = 1;
else C[i][j] = moc(C[i - 1][j] + C[i - 1][j - 1]);
}
int main() {
init();
int T;
scanf("%d", &T);
for(int j = 1; j <= T; j++){
int n, m, k, sum = 0;
int ans = 0;
scanf("%d%d%d", &n, &m, &k);
for(int s = 0; s < 16; s++){
int b = 0, r = n, c = m;
if(s & 1) {r--, b++;}
if(s & 2) {r--, b++;}
if(s & 4) {c--, b++;}
if(s & 8) {c--, b++;}
if(b&1) ans = (mod - C[r*c][k] + ans) % mod;
else ans = moc(ans + C[r*c][k]);
}
printf("Case %d: %d\n", j, ans);
}
}
UVA1374 Power Calculus 迭代搜索

两个剪枝:如果以指数增长不可以满足,就byebye;
数不会超过2*n;

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
using namespace std;
#define ll long long
const int M = 2e5 + 10;
int n;
int a[2005] = {0, 1}, fg;
void dfs(int up, int dep){
if(a[dep] == n){
fg = dep-1; return ;
}
if(a[dep] <<(up-dep+1) < n) return ;
if(dep > up) return;
for(int i = 1; i <= dep; i++){
if(fg) return ;
int t = a[dep] + a[i];
if(t > 0 && t <= 2*n){
a[dep+1] = t;
dfs(up, dep+1);
}
t = a[dep] - a[i];
if(t > 0 && t <= 2*n){
a[dep+1] = t;
dfs(up, dep+1);
}
}
}
int main(){
while(scanf("%d", &n)&&n){
fg = 0; int i = 1;
if(n == 1) {printf("0\n");continue;}
while(1){
dfs(i, 1);
if(fg)break;
i++;
}
printf("%d\n",i);
}
}
UVA1394 And Then There Was One 经典的猴子报数 思维
题意:最初,n个石头按照顺时针的顺序围成一个圈,它们的编号是1,...,n.现在你将会得到两个数字k和m。之后,移除石子m,然后数k个石子移除一个,重复这个操作直到只剩下一个石子为止,求这个最后剩下的石子的编号。(与约瑟夫问题类似)
题解:
UVA1481 Genome Evolution 计算几何 思维+代码
题目大意:给你n个点和一个m×m的坐标纸(坐标范围0-m-1),n个点中前两个为A和B,要求给出坐标纸上满足以下性质的点的数目——某一个点满足条件当且仅当对任意一个给定点C,它对A曼哈顿距离小于C对A曼哈顿距离 或 它对B曼哈顿距离小于C对B曼哈顿距离。
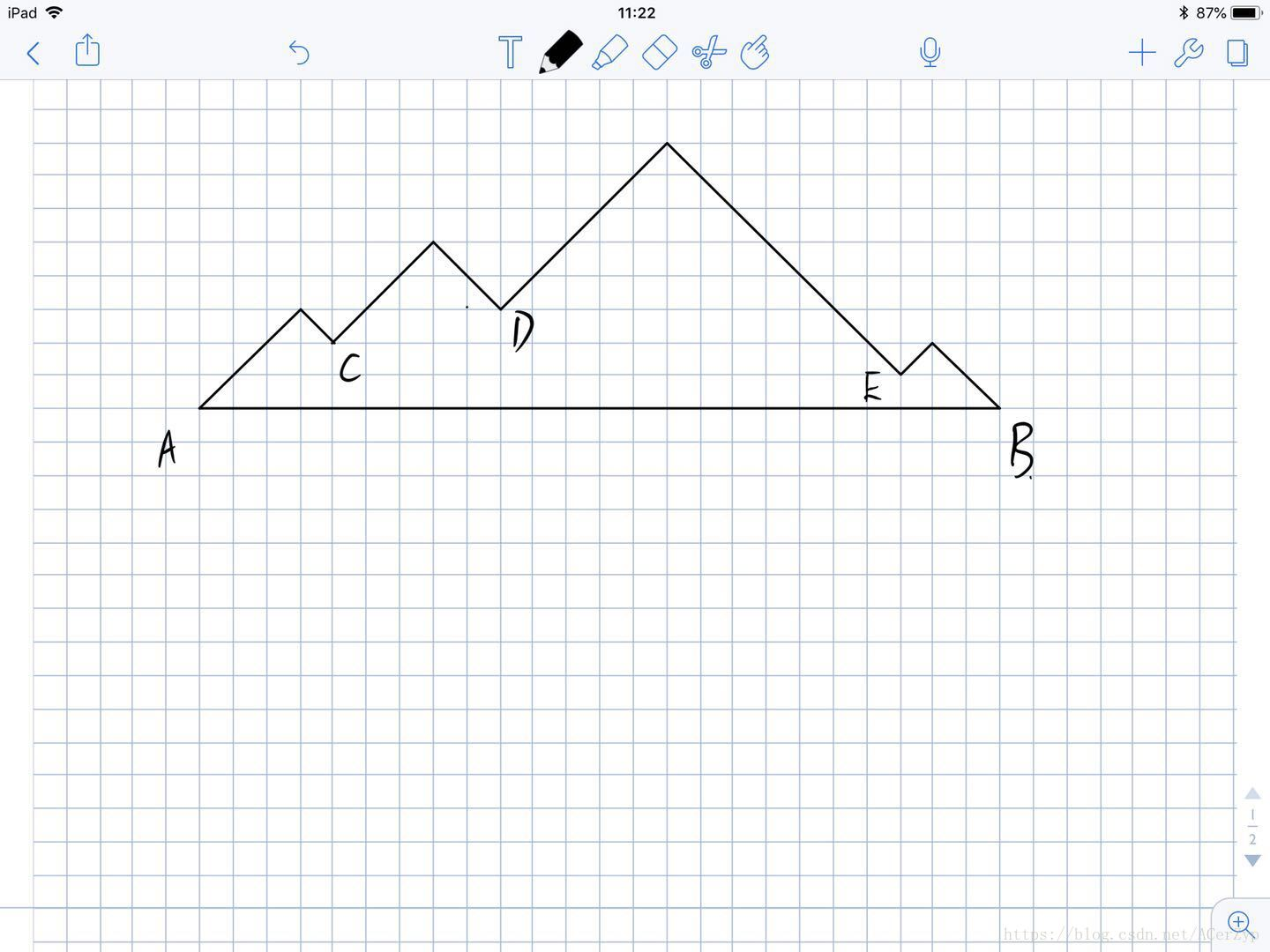
思路:显然符合条件的点都在AB之间(因为如果在AB两侧则假设此点在A左侧,则此点到A距离小于A,到B距离也小于B,不符合题意)。则对于任意一个题目输入的点,它的可行域(即对于此点符合条件的点的集合)如下:

则整个题目给定点的可行域为所有单个点可行域的交集,则大致如下图:

#include<bits/stdc++.h> using namespace std; const int M = 1e5 + 5, INF = 2e9; int b[M], a[M], pos[M]; int read(){ int x = 0; int f = 1; char c = getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();} return x*=f; } int up[M]; inline int ab(int a){return a>=0?a:-a;} int main(){ int n; while(scanf("%d", &n)&&n){ for(int i = 1; i <= n; i++) a[i] = read(); for(int i = 1; i <= n; i++) b[i] = read(), pos[b[i]] = i; int cnt = 0; for(int st = 1; st < n; st++){ int lf = pos[a[st]], rg = pos[a[st]], L = lf, R = rg; for(int ed = st + 1; ed <= n; ed++){ int x = pos[a[ed]]; if(x < lf) lf = x; if(x > rg) rg = x; if(L > lf) L--; else R++; if(L == lf && rg == R) cnt++; } } printf("%d\n",cnt); } }
uva 11400 lighting system design 贪心+DP 思维
题目大意:给出n个模式,每个模式有电压v,电压费用k,每盏灯的花费c以及灯数l。然后电压高的可以用于电压低得。问说最少花费多少钱可以满足n个模式。
题解:首先贪心,对于每种灯泡要不然全换,要不然全不换,费用节省主要是由于替换灯泡类型而排除了低压电源,将灯泡按电压上升排序,DPi表示考虑了前i个灯泡的最优解,我就只需要枚举之前是哪换的,DPj是有许多种灯泡组成的,所以用它更新考虑了替换不同电压灯泡的情况,相当于灯泡先换成j,再换为i.
uva Fewest Flops 贪心+DP状态定义 思维
题意:输入一个正整数 k 和一个字符串 S, 字符串的长度保证为 k 的整数倍。把 S 的字符串从左至右的顺序每 k 个分成一组,每组里面的字符串可以任意重排,但组与组间的顺序不能改变。你的任务是使重排后的字符串包含的 “块”
尽量的少,每个 “块” 为连续的相同的字母。比如 uuvuwwuv 可以分为两组:uuvu 和 wwuv,第一组重排为 uuuv , 第二组重排为 vuww,连接起来就是 uuuvvuww, 包含4个 “块”。
思路:
dp[i][j]: 第 i 块以第 j 位结尾时的最小块数
对于每个单独的一块,它的chunks就是等于出现的不同字母数
第 i 块的chunks记做 chunks[i]
如果第 i-1 块的最后一位和第 i 块的第一位是一样的,那么可以合并这两个,总chunks可以减少一个
dp[i][j] = min{ 如果i-1块的第k位和i块的第一位不同:dp[i-1][k]+chunks[i],
如果i-1块的第k位和i块的第一位相同: dp[i-1][k]+chunks[i]-1 }

#include <iostream> #include <cstring> #include <cmath> #include <string> #include <algorithm> #include <queue> #include <stack> using namespace std; const int INF = 1<<29; const double PI = acos(-1.0); const double e = 2.718281828459; const double eps = 1e-8; const int MAXN = 1010; int vis[256]; char s[MAXN]; int dp[MAXN][MAXN]; int main() { //freopen("in.txt", "r", stdin); //freopen("out.txt", "w", stdout); int Case, kk, chunk; cin>>Case; while(Case--) { cin>>kk>>s; int len = strlen(s); for(int i = 0; i < len/kk; i++) { fill(dp[i], dp[i]+kk, INF); memset(vis, 0, sizeof(vis)); chunk = 0; for(int j = i*kk; j <= (i+1)*kk-1; j++) { if(!vis[s[j]]) { vis[s[j]] = 1; chunk++; } } if(!i) { for(int j = 0; j < kk; j++) dp[i][j] = chunk; continue; } for(int j = 0; j < kk; j++) { for(int k = 0; k < kk; k++) { // 在第 i-1 块里面选择第 k 位的字母,作为第 i-1 块的末位,同时作为第 i 块的首位 int front = (i-1)*kk+k; int rear = i*kk+j;// 在第 i 块里面选择第 j 位的字母,作为第 i 块的末位 if(vis[s[front]] && (chunk==1||s[front]!=s[rear])) //第 i 块的首位和末位不可能为同个字母,除非第 i 块的所有字母都相同 dp[i][j] = min(dp[i][j], dp[i-1][k]+chunk-1); else dp[i][j] = min(dp[i][j], dp[i-1][k]+chunk); } } } int ans = INF; for(int i = 0; i < kk; i++) ans = min(ans, dp[len/kk-1][i]); cout<<ans<<endl; } return 0; }
UVA1169 Robotruck 线段树、单调队列优化DP
题目描述】
有n个垃圾,第i个垃圾的坐标为(xi,yi),重量为wi。有一个机器人,要按照编号从小到大的顺序捡起所有垃圾并扔进垃圾桶(垃圾桶在原点(0,0))。机器人可以捡起几个垃圾以后一起扔掉,但任何时候其手中的垃圾总重量不能超过最大载重C。两点间的行走距离为曼哈顿距离(即横坐标之差的绝对值加上纵坐标之差的绝对值)。求出机器人行走的最短总路程(一开始,机器人在(0,0)处)。
【输入格式】
输入的第一行为数据组数。每组数据的第一行为最大承重C(1<=C<=100);第二行为正整数n(1<=n<=100000),即垃圾的数量;以下n行每行为两个非负整数x,y和一个正整数w,即坐标和重量(重量保证不超过C)。
【输出格式】
对于每组数据,输出总路径的最短长度。

这个可以线段树优化;

#include<bits/stdc++.h> using namespace std; const int M = 1e5 + 5, INF = 2e9; int dis[M], sum[M], x[M], y[M], ls[M], c[M], dp[M]; inline int ab(int a){return a >= 0 ? a : -a;} int n, C; struct Node{ int v; Node *ls, *rs; void up(){ v = min(ls->v, rs->v); } }pool[M << 2], *root, *tail = pool; #define Ls nd->ls, lf, mid #define Rs nd->rs, mid+1, rg Node *build(int lf = 0, int rg = n){ Node *nd = ++tail; if(lf == rg)nd->v = INF; else { int mid = (lf + rg) >> 1; nd->ls = build(lf, mid); nd->rs = build(mid+1, rg); nd->up(); } return nd; } void add(int pos, int d, Node *nd = root, int lf = 0, int rg = n){ if(lf == rg)nd->v = d; else { int mid = (lf + rg) >> 1; if(pos <= mid) add(pos, d, Ls); else add(pos, d, Rs); nd->up(); } return ; } int query(int L, int R, Node *nd = root, int lf = 0, int rg = n){ if(L <= lf && rg <= R) return nd->v; int mid = (lf + rg) >> 1; int ans = INF; if(L <= mid) ans = query(L, R, Ls); if(R > mid) ans = min(ans, query(L, R, Rs)); return ans; } int read(){ int x = 0; int f = 1; char c = getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();} return x*=f; } int main(){ int T = read(); while(T--){ C = read(); n = read(); tail = pool; root = build(); int lst = 0; for(int i = 1; i <= n; i++){ x[i] = read(), y[i] = read(), c[i] = read(); sum[i] = sum[i - 1] + c[i]; while(sum[i] - sum[lst] > C) lst++; ls[i] = lst; dis[i] = dis[i - 1] + ab(x[i] - x[i-1]) + ab(y[i] - y[i-1]); } dp[0] = 0; add(0, 0); for(int i = 1; i <= n; i++){ dp[i] = query(ls[i], i - 1) + x[i] + y[i] + dis[i]; add(i, dp[i] - dis[i+1] + x[i+1] + y[i+1]); } printf("%d\n", dp[n]); if(T > 0) printf("\n"); } }
UVA10891 Game of Sum DP重复状态优化
题目描述
有一个长度为n的整数序列,两个游戏者A和B轮流取数,A先取。每次玩家只能从左端或者右端取任意数量的数,但不能两边都取。所有数都被取走视为游戏结束,然后统计每个人取走的数之和,作为各自的得分。两个人采取的策略都是让自己得分尽可能高,并且两个人都很机智,求A得分-B得分后的结果。 输入格式
输入包含多组数据,每组数据第一行为正整数n(1<=n<=100) ,第二行为给定的整数序列,输入结束标志是n=0 输出格式
对于每组数据,输出A和B都采取最优策略下,A的得分-B的得分

#include<bits/stdc++.h> using namespace std; const int M = 105, INF = 2e9; int sum[M], a[M]; int read(){ int x = 0; int f = 1; char c = getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();} return x*=f; } int dp[M][M], g[M][M], f[M][M]; int main(){ // freopen("c.in","r",stdin); // freopen("c.out","w",stdout); int n, cas = 0; while(scanf("%d",&n) && n){ for(int i = 1; i <= n; i++) { a[i] = read(), sum[i] = sum[i - 1] + a[i]; dp[i][i] = f[i][i] = g[i][i] = a[i]; } for(int l = 2; l <= n; l++){ for(int i = 1; i + l - 1 <= n; i++){ int j = i + l - 1; int m = 0; m = min(m, min(f[i+1][j], g[i][j-1])); dp[i][j] = sum[j] - sum[i-1] - m; f[i][j] = min(f[i+1][j], dp[i][j]); g[i][j] = min(g[i][j-1], dp[i][j]); //printf("%d %d %d\n",i,j,dp[i][j]); } } printf("%d\n", 2*dp[1][n] - sum[n]); } }
UVA11825 Hackers' Crackdown 数学模型 代码+思维
题目描述
假如你是一个黑客,侵入了一个有着n台计算机(编号为1.2.3....n)的网络。一共有n种服务,每台计算机都运行着所有服务。对于每台计算机,你都可以选择一项服务,终止这台计算机和所有与它相邻计算机的该项服务(如果其中一些服务已经停止,那他们继续保持停止状态)。你的目标是让尽量多的服务完全瘫痪(即:没有任何计算及运行着该服务) 输入格式
输入包含多组数据,每组数据的第一行为整数n(1<=n<=16):以下n行每行描述一台计算机相邻的计算机,其中第一个数m为相邻计算机个数,接下来的m个整数为这些计算机的编号。输入结束标志n=0. 输出格式
对于每组数据,输出完全瘫痪的服务的数量


#include<bits/stdc++.h> using namespace std; const int M = (1<<16) + 1, INF = 2e9; int read(){ int x = 0; int f = 1; char c = getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();} return x*=f; } int f[M], cover[M], P[M]; int main(){ int n, cas = 0; while(scanf("%d",&n) && n){ memset(P, 0, sizeof(P)); memset(cover, 0, sizeof(cover)); memset(f, 0x8f, sizeof(f)); ++cas; for(int i = 0; i < n; i++){ int m = read(); P[i] |= (1<<i); while(m--){ int x = read(); P[i] |= (1<<x); } } int all = (1<<n) - 1; for(int s = 0; s <= all; s++) for(int i = 0; i < n; i++) if(s&(1<<i)) cover[s] |= P[i]; f[0] = 0; for(int S = 0; S <= all; S++) for(int S0 = S; S0; S0 = S&(S0-1)){ if(cover[S0] == all) f[S] = max(f[S], f[S^S0] + 1); } printf("Case %d: %d\n", cas, f[all]); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号