BFS简单题记
围成面积
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1359时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
编程计算由“*”号围成的下列图形的面积。面积计算方法是统计*号所围成的闭合曲线中水平线和垂直线交点的数目。如下图所示，在10*10的二维数组中，有“*”围住了15个点，因此面积为15。
【输入】
10×10的图形。
【输出】
输出面积。
【输入样例】
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
【输出样例】
15
题解：注意可能有多个区域被圈起来
#include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; int a[105]; bool b[105]; int zl[4][2]={{0,1},{0,-1},{1,0},{-1,0}}; int mp[15][15]; struct node{ int x,y; node():x(),y(){} node(const int x,const int y):x(x),y(y){} }; queue <node>Q; int t=1,ans; void bfs(int x,int y) { mp[x][y]=++t; a[t]++; Q.push(node(x,y)); while(!Q.empty()) { node u=Q.front(); Q.pop(); for(int i=0;i<4;i++) { int xx=u.x+zl[i][0],yy=u.y+zl[i][1]; if(xx>0&&xx<=10&&yy>0&&yy<=10&&!mp[xx][yy]) { mp[xx][yy]=t; a[t]++; Q.push(node(xx,yy)); } } } } int main() { for(int i=1;i<=10;i++) for(int j=1;j<=10;j++) cin>>mp[i][j]; for(int i=1;i<=10;i++) for(int j=1;j<=10;j++) if(!mp[i][j]) bfs(i,j); for(int i=1;i<=10;i++)b[mp[i][1]]=1; for(int i=1;i<=10;i++)b[mp[i][10]]=1; for(int i=1;i<=10;i++)b[mp[10][i]]=1; for(int i=1;i<=10;i++)b[mp[1][i]]=1; for(int i=2;i<=9;i++) for(int j=2;j<=9;j++) if(!b[mp[i][j]]&&mp[i][j]!=1) { b[mp[i][j]]=1; ans+=a[mp[i][j]]; } cout<<ans<<endl; }
奇怪的电梯(lift)
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1360时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
大楼的每一层楼都可以停电梯，而且第i层楼（1<=i<=N）上有一个数字Ki（0<=Ki<=N）。电梯只有四个按钮：开，关，上，下。上下的层数等于当前楼层上的那个数字。当然，如果不能满足要求，相应的按钮就会失灵。例如：3 3 1 2 5代表了Ki（K1=3,K2=3,……），从一楼开始。在一楼，按“上”可以到4楼，按“下”是不起作用的，因为没有-2楼。那么，从A楼到B楼至少要按几次按钮呢？
【输入】
共有二行，第一行为三个用空格隔开的正整数，表示N,A,B(1≤N≤200, 1≤A,B≤N)，第二行为N个用空格隔开的正整数，表示Ki。
【输出】
一行，即最少按键次数,若无法到达，则输出-1。
【输入样例】
5 1 5 3 3 1 2 5
【输出样例】
3
#include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; int a[205],c[205]; bool b[205]; int N,A,B; queue <int>Q; int bfs() { Q.push(A); b[A]=1; while(!Q.empty()) { int u=Q.front(); Q.pop(); int x=u+a[u],y=u-a[u]; if(x>0&&x<=N&&!b[x]) { b[x]=1;Q.push(x);c[x]=c[u]+1; } if(y>0&&y<=N&&!b[y]) { b[y]=1;Q.push(y);c[y]=c[u]+1; } if(b[B])return 1; } return 0; } int main() { cin>>N>>A>>B; for(int i=1;i<=N;i++)cin>>a[i]; if(bfs())cout<<c[B]<<endl; else cout<<"-1"<<endl; }
产生数(Produce)
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1361时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
给出一个整数n（n<=2000）和k个变换规则（k≤15）。规则：
① 1个数字可以变换成另1个数字；
② 规则中，右边的数字不能为零。
例如：n=234，k=2规则为
2 → 5
3 → 6
上面的整数234经过变换后可能产生出的整数为（包括原数）234，534，264，564共4种不同的产生数。
求经过任意次的变换（0次或多次），能产生出多少个不同的整数。仅要求输出不同整数个数。
【输入】
n
k
x1 y1
x2 y2
… …
xn yn
【输出】
格式为一个整数（满足条件的整数个数）。
【输入样例】
234 2 2 5 3 6
【输出样例】
4
题解：方案数=第1位可变化的方案*第2位可变化的方案*……*第n-1位可变化的方案*第n位可变化的方案
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<vector>
using namespace std;
int a[25];
bool b[12];
queue <int>Q;
vector<int>G[15];
int bfs(int x)
{
int t=1;
Q.push(x);
b[x]=1;
while(!Q.empty())
{
int u=Q.front();
Q.pop();
for(int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if(!b[v])
{
t++;Q.push(v);b[v]=1;
}
}
}
return t;
}
int main()
{
string s;
int ans=1,k;
cin>>s>>k;
for(int i=1;i<=k;i++)
{
int u,v;
cin>>u>>v;
G[u].push_back(v);
}
for(int i=0;i<s.size();i++)
{
memset(b,0,sizeof(b));
ans*=bfs(s[i]-'0');
}
cout<<ans<<endl;
}
【例8.3】最少步数
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1330时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
在各种棋中，棋子的走法总是一定的，如中国象棋中马走“日”。有一位小学生就想如果马能有两种走法将增加其趣味性，因此，他规定马既能按“日”走，也能如象一样走“田”字。他的同桌平时喜欢下围棋，知道这件事后觉得很有趣，就想试一试，在一个（100*100）的围棋盘上任选两点A、B，A点放上黑子，B点放上白子，代表两匹马。棋子可以按“日”字走，也可以按“田”字走，俩人一个走黑马，一个走白马。谁用最少的步数走到左上角坐标为(1,1)的点时，谁获胜。现在他请你帮忙，给你A、B两点的坐标，想知道两个位置到（1,1）点可能的最少步数。
【输入】
A、B两点的坐标。
【输出】
最少步数。
【输入样例】
12 16 18 10
【输出样例】
8 9
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;
int zl[12][2]={{1,2},{1,-2},{-1,2},{-1,-2},{-2,-1},{-2,1},{2,1},{2,-1},{2,2},{-2,-2},{2,-2},{-2,2}};
int Ax,Ay,Bx,By;
bool mp[105][105];
struct node{
int x,y,step;
node(){}
node(const int x,const int y,const int step):x(x),y(y),step(step){}
};
int bfs(int u,int v)
{
queue <node>Q;
Q.push(node(u,v,0));
mp[u][v]=1;
while(!Q.empty())
{
node nw=Q.front();
Q.pop();
for(int i=0;i<12;i++)
{
int x=nw.x+zl[i][0],y=nw.y+zl[i][1];
if(x>0&&x<=100&&y>0&&y<=100&&!mp[x][y])
{
Q.push(node(x,y,nw.step+1));
mp[x][y]=1;
if(x==1&&y==1)return nw.step+1;
}
}
}
return -1;
}
int main()
{
cin>>Ax>>Ay>>Bx>>By;
cout<<bfs(Ax,Ay)<<endl;
memset(mp,0,sizeof(mp));
cout<<bfs(Bx,By)<<endl;
}
仙岛求药
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1251
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
少年李逍遥的婶婶病了，王小虎介绍他去一趟仙灵岛，向仙女姐姐要仙丹救婶婶。叛逆但孝顺的李逍遥闯进了仙灵岛，克服了千险万难来到岛的中心，发现仙药摆在了迷阵的深处。迷阵由M×N个方格组成，有的方格内有可以瞬秒李逍遥的怪物，而有的方格内则是安全。现在李逍遥想尽快找到仙药，显然他应避开有怪物的方格，并经过最少的方格，而且那里会有神秘人物等待着他。现在要求你来帮助他实现这个目标。
下图 显示了一个迷阵的样例及李逍遥找到仙药的路线。
【输入】
输入有多组测试数据. 每组测试数据以两个非零整数 M 和 N 开始，两者均不大于20。M 表示迷阵行数, N 表示迷阵列数。接下来有 M 行, 每行包含N个字符,不同字符分别代表不同含义:
1)‘@’：少年李逍遥所在的位置；
2)‘.’：可以安全通行的方格；
3)‘#’：有怪物的方格；
4)‘*’：仙药所在位置。
当在一行中读入的是两个零时，表示输入结束。
【输出】
对于每组测试数据，分别输出一行，该行包含李逍遥找到仙药需要穿过的最少的方格数目(计数包括初始位置的方块)。如果他不可能找到仙药, 则输出 -1。
【输入样例】
8 8 .@##...# #....#.# #.#.##.. ..#.###. #.#...#. ..###.#. ...#.*.. .#...### 6 5 .*.#. .#... ..##. ..... .#... ....@ 9 6 .#..#. .#.*.# .####. ..#... ..#... ..#... ..#... #.@.## .#..#. 0 0
【输出样例】
10 8 -1
#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int qx,qy,m,n;
const int zl[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
char mp[25][25];
struct node{
int x,y,step;
node():x(),y(),step(){}
node(const int x,const int y,const int step):x(x),y(y),step(step){}
};
void bfs()
{
queue <node> Q;
Q.push(node(qx,qy,0));
mp[qx][qy]='#';
while(!Q.empty())
{
node nw=Q.front();
Q.pop();
for(int i=0;i<4;i++)
{
int x1=nw.x+zl[i][0],yy1=nw.y+zl[i][1];
if(x1>=0&&x1<m&&yy1>=0&&yy1<n&&(mp[x1][yy1]=='*'||mp[x1][yy1]=='.'))
{
if(mp[x1][yy1]=='*')
{
cout<<nw.step+1<<endl;
return ;
}
Q.push(node(x1,yy1,nw.step+1));
mp[x1][yy1]='#';
}
}
}
cout<<"-1"<<endl;
}
int main()
{
while(cin>>m>>n)
{
if(!m&&!n)break;
for(int i=0;i<m;i++)
{
scanf("%s",mp[i]);
for(int j=0;j<n;j++)
if(mp[i][j]=='@')
{
qx=i;qy=j;
}
}
bfs();
}
}
Dungeon Master
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1248
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
这题是一个三维的迷宫题目，其中用‘.’表示空地，‘#’表示障碍物，‘S’表示起点，‘E’表示终点，求从起点到终点的最小移动次数，解法和二维的类似，只是在行动时除了东南西北移动外还多了上下。可以上下左右前后移动，每次都只能移到相邻的空位，每次需要花费一分钟，求从起点到终点最少要多久。
【输入】
多组测试数据。
一组测试测试数据表示一个三维迷宫：
前三个数，分别表示层数、一个面的长和宽，后面是每层的平面图。前三个数据为三个零表示结束。
【输出】
最小移动次数。
【输入样例】
3 4 5 S.... .###. .##.. ###.# ##### ##### ##.## ##... ##### ##### #.### ####E 1 3 3 S## #E# ### 0 0 0
【输出样例】
Escaped in 11 minute(s). Trapped!
【提示】
对于题目给出数据的含义就是输入l，r，c，分别代表迷宫有l层，每层长宽分别是c，r。对于数据以可以这样移动:
(1,1,1)->(1,1,2)->(1,1,3)->(1,1,4)->(1,1,5)->(1,2,5)->
(1,3,5)->(1,3,4)->(1,4,4)->(2,4,4)->(2,4,5)->(3,4,,5)
共11步就可以到达终点 对于数据二明显不能到达，则输出Trapped！
这题用BFS解，每次去队首元素，如果是终点则输出结果移动的次数，否则，从该点开始分别向东南西北上下移动（如果可以走的话）并继续搜，如果到队列为空还没搜到解法，则说明无解。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
int L,r,c,qx,qy,qz;
const int maxn=105;
char mp[maxn][maxn][maxn];
int x1[7]={0,0,0,0,1,-1};
int y1[7]={1,-1,0,0,0,0};
int z1[7]={0,0,1,-1,0,0};
struct node
{
int z,x,y,step;
node ():z(),x(),y(),step(){}
node (const int z,const int x,const int y,const int step):z(z),x(x),y(y),step(step){}
};
void bfs()
{
queue <node>Q;
Q.push(node(qz,qx,qy,0));
mp[qz][qx][qy]='#';
while(!Q.empty())
{
node nw=Q.front();
Q.pop();
for(int i=0;i<7;i++)
{
int zn=nw.z+z1[i],xn=nw.x+x1[i],yy1=nw.y+y1[i];
if(zn>=0&&zn<L&&xn>=0&&xn<r&&yy1>=0&&yy1<c&&(mp[zn][xn][yy1]=='.'||mp[zn][xn][yy1]=='E'))
{
if(mp[zn][xn][yy1]=='E')
{
printf("Escaped in %d minute(s).\n",nw.step+1);
return ;
}
Q.push(node(zn,xn,yy1,nw.step+1));
mp[zn][xn][yy1]='#';
}
}
}
cout<<"Trapped!"<<endl;
}
int main()
{
while(cin>>L>>r>>c)
{
if(r==0&&L==0&&c==0)break;
memset(mp,0,sizeof(mp));
char a;
for(int i=0;i<L;i++)
for(int j=0;j<r;j++)
{
scanf("%s",mp[i][j]);
for(int m=0;m<c;m++)
if(mp[i][j][m]=='S')
{
qz=i;qx=j;qy=m;
}
}
bfs();
}
}
Knight Moves
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1257
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
输入n代表有个n*n的棋盘，输入开始位置的坐标和结束位置的坐标，问一个骑士朝棋盘的八个方向走马字步，从开始坐标到结束坐标可以经过多少步。
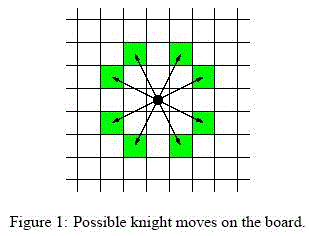
【输入】
首先输入一个n,表示测试样例的个数。
每个测试样例有三行。
第一行是棋盘的大小L(4<=L<=300);
第二行和第三行分别表示马的起始位置和目标位置（0~L-1）。
【输出】
马移动的最小步数，起始位置和目标位置相同时输出0。
【输入样例】
3 8 0 0 7 0 100 0 0 30 50 10 1 1 1 1
【输出样例】
5 28 0
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
int n,qx,qy,ex,ey;
int a[8][2]={{1,2},{-1,2},{-2,1},{2,1},{-1,-2},{1,-2},{-2,-1},{2,-1}};
int mp[305][305];
struct node
{
int x,y,step;
node ():x(),y(),step(){}
node (const int x,const int y,const int step):x(x),y(y),step(step){}
};
void bfs()
{
queue <node>Q;
Q.push(node(qx,qy,0));
mp[qx][qy]=-1;
while(!Q.empty())
{
node nw=Q.front();
Q.pop();
for(int i=0;i<8;i++)
{
int xn=nw.x+a[i][0],yy1=nw.y+a[i][1];
if(xn>=0&&xn<n&&yy1>=0&&yy1<n&&mp[xn][yy1]==0)
{
if(xn==ex&&yy1==ey)
{
printf("%d\n",nw.step+1);
return ;
}
Q.push(node(xn,yy1,nw.step+1));
mp[xn][yy1]=-1;
}
}
}
cout<<"0"<<endl;
}
int main()
{
int t;
cin>>t;
while(t--)
{
cin>>n;
cin>>qx>>qy>>ex>>ey;
if(qx==ex&&qy==ey)
{
cout<<"0"<<endl;return 0;
}
memset(mp,0,sizeof(mp));
bfs();
}
}
抓住那头牛
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1253
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
农夫知道一头牛的位置，想要抓住它。农夫和牛都位于数轴上，农夫起始位于点N(0<=N<=100000)，牛位于点K(0<=K<=100000)。农夫有两种移动方式：
1、从X移动到X-1或X+1，每次移动花费一分钟
2、从X移动到2*X，每次移动花费一分钟
假设牛没有意识到农夫的行动，站在原地不动。农夫最少要花多少时间才能抓住牛？
【输入】
两个整数，N和K。
【输出】
一个整数，农夫抓到牛所要花费的最小分钟数。
【输入样例】
5 17
【输出样例】
4
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int zl[3]={1,-1},m[1000006];
int n,k;
void bfs()
{
queue <int>Q;
Q.push(n);
while(!Q.empty())
{
int x=Q.front();
Q.pop();
for(int i=0;i<3;i++)
{
int x1;
if(i==2)x1=2*x;
else x1=x+zl[i];
if(x1>=0&&x1<=100005&&!m[x1])
{
if(x1==k)
{
cout<<m[x]<<endl;return ;
}
m[x1]=m[x]+1;
Q.push(x1);
}
}
}
}
int main()
{
cin>>n>>k;
m[n]=1;
bfs();
}
The Castle
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1250
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
一座城堡被分成ｍ*ｎ个方块（m≤50，n≤50），每个方块可有0～4堵墙（0表示无墙）。下面示出了建筑平面图：
图中的加粗黑线代表墙。几个连通的方块组成房间，房间与房间之间一定是用黑线（墙）隔开的。
现在要求你编一个程序，解决以下2个问题：
1、该城堡中有多少个房间?
2、最大的房间有多大?
【输入】
平面图用一个数字表示一个方块(第1个房间用二进制1011表示，0表示无东墙，用十进制11表示)。
第一行一个整数m（m≤50），表示房子南北方向的长度。
第二行一个整数n（n≤50），表示房子东西方向的长度。
后面的m行，每行有n个整数，每个整数都表示平面图对应位置的方块的特征。每个方块中墙的特征由数字P来描述（0≤P≤15）。数字P是下面的可能取的数字之和：
1（西墙 west）
2（北墙 north）
4（东墙 east）
8（南墙 south）
室内的墙被定义两次： 例如方块（1，1）中的南墙也被位于其南面的方块（2，1）定义了一次。
建筑中至少有两个房间。
【输出】
第1行：一个整数，表示房间总数；
第2行：一个整数，表示最大房间的面积（方块数）。
【输入样例】
4 7 11 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13
【输出样例】
5 9
题解：mp[i][j][0]记录是第几个房间，mp[i][j][1..4]记录该方向是否有障碍
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int n,m,ans;
int mp[255][255][6];
struct node{
int x,y;
node():x(),y(){}
node(const int x,const int y):x(x),y(y){}
};
int zl[5][2]={{0},{0,-1},{-1,0},{0,1},{1,0}};
int a[5]={0,1,2,4,8};
void bfs(int x,int y,int t)
{
queue <node>Q;
Q.push(node(x,y));
ans++;
mp[x][y][0]=t;
while(!Q.empty())
{
node nw=Q.front();
Q.pop();
for(int i=1;i<=4;i++)
{
int x1=nw.x+zl[i][0],yy1=nw.y+zl[i][1];
if(x1>0&&x1<=m&&yy1>0&&yy1<=n&&!mp[nw.x][nw.y][i]&&!mp[x1][yy1][0])
{
mp[x1][yy1][0]=t;
Q.push(node(x1,yy1));
ans++;
}
}
}
}
int main()
{
cin>>m>>n;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
int p;
cin>>p;
for(int k=4;k>0;k--)
if(p-a[k]>=0)
{
p-=a[k];
mp[i][j][k]=1;
}
}
int t=1,maxn=0;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(!mp[i][j][0])
{
bfs(i,j,t++);
maxn=max(maxn,ans);
ans=0;
}
cout<<t-1<<endl<<maxn<<endl;
}
Lake Counting
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1249
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
题意：有一块N*M的土地，雨后积起了水，有水标记为‘W’，干燥为‘.’。八连通的积水被认为是连接在一起的。请求出院子里共有多少水洼？
【输入】
第一行为N,M(1<=N,M<=110)。
下面为N*M的土地示意图。
【输出】
一行，共有的水洼数。
【输入样例】
10 12 W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W.
【输出样例】
3
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int n,m;
int mp[115][115];
queue <int> Q;
int a[8][2]={{0,1},{0,-1},{1,0},{-1,0},{1,-1},{-1,1},{-1,-1},{1,1}};
//包括斜的
void bfs(int k)
{
while(!Q.empty())
{
int x=Q.front();Q.pop();
int y=Q.front();Q.pop();
for(int i=0;i<8;i++)
{
int x1=x+a[i][0];
int yy1=y+a[i][1];
if(x1>0&&x1<=n&&yy1>0&&yy1<=m&&mp[x1][yy1]==0)
{
Q.push(x1);Q.push(yy1);
mp[x1][yy1]=k;
}
}
}
}
int main()
{
int ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
char a;
cin>>a;
if(a=='.')mp[i][j]=-1;
}
int k=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(!mp[i][j])
{
Q.push(i);Q.push(j);
mp[i][j]=++k;
bfs(k);
}
}
cout<<k<<endl;
}
迷宫问题
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1255
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
定义一个二维数组：
int maze[5][5] = {
0,1,0,0,0,
0,1,0,1,0,
0,0,0,0,0,
0,1,1,1,0,
0,0,0,1,0,
};
它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
【输入】
一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。
【输出】
左上角到右下角的最短路径，格式如样例所示。
【输入样例】
0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0
【输出样例】
(0, 0) (1, 0) (2, 0) (2, 1) (2, 2) (2, 3) (2, 4) (3, 4) (4, 4)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
queue <int> Q;
int a[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
int mp[6][6];
int j[6][6][2];
int bfs()
{
int flag=0;
while(!Q.empty())
{
if(flag)return 0;
int x=Q.front();Q.pop();
int y=Q.front();Q.pop();
for(int i=0;i<4;i++)
{
int x1=x+a[i][0],yy1=y+a[i][1];
if(x1>0&&x1<6&&yy1>0&&yy1<6&&!mp[x1][yy1])
{
mp[x1][yy1]=mp[x][y]+1;
j[x1][yy1][0]=x;j[x1][yy1][1]=y;
if(x1==5&&yy1==5){
flag=1;break;
}
Q.push(x1);Q.push(yy1);
}
}
}
}
int show(int x,int y)
{
if(x==1&&y==1)return 0;
show(j[x][y][0],j[x][y][1]);
printf("(%d, %d)\n",j[x][y][0]-1,j[x][y][1]-1);
}
int main()
{
for(int i=1;i<6;i++)
for(int j=1;j<6;j++)
{
cin>>mp[i][j];
if(mp[i][j])mp[i][j]=-1;
}
Q.push(1);Q.push(1);
mp[1][1]=1;
bfs();
show(5,5);
printf("(4, 4)\n");
}
流感传染
链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1191时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
有一批易感人群住在网格状的宿舍区内，宿舍区为n*n的矩阵，每个格点为一个房间，房间里可能住人，也可能空着。在第一天，有些房间里的人得了流感，以后每天，得流感的人会使其邻居传染上流感，（已经得病的不变），空房间不会传染。请输出第m天得流感的人数。
【输入】
第一行一个数字n，n不超过100，表示有n*n的宿舍房间。
接下来的n行，每行n个字符，’.’表示第一天该房间住着健康的人，’#’表示该房间空着，’@’表示第一天该房间住着得流感的人。
接下来的一行是一个整数m，m不超过100。
【输出】
输出第m天，得流感的人数。
【输入样例】
5 ....# .#.@. .#@.. #.... ..... 4
【输出样例】
16
#include<iostream>
#include<cstdio>
#include<string>
#include<queue>
using namespace std;
struct node{
int x,y,num;
};
queue <node> Q;
char a[105][105];
int mp[105][105];
int p[4][2]={{0,-1},{0,1},{1,0},{-1,0}};
int n,t;
void dfs(int t){
while(!Q.empty())
{
node now=Q.front();Q.pop();
for(int i=0;i<4;i++)
{
node s;
s.x=now.x+p[i][0];
s.y=now.y+p[i][1];
s.num=now.num+1;
if(s.num>t)return;
if(s.x>0&&s.x<=n&&s.y>0&&s.y<=n&&mp[s.x][s.y]==0)
{
mp[s.x][s.y]=1;
Q.push(s);
}
}
}
}
int main()
{
int cnt=0,k=0;
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
if(a[i][j]=='#')mp[i][j]=-1;
if(a[i][j]=='@')
{
mp[i][j]=1;
node s;
s.x=i;s.y=j;s.num=1;
Q.push(s);
}
}
cin>>t;
dfs(t);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(mp[i][j]==1)cnt++;
cout<<cnt<<endl;
}
小浣熊松松和朋友到野外露营，没想到遇上了π年一次的大洪水，好在松松是一只爱观察的小浣熊，他发现露营地的地形和洪水有如下性质：
①露营地可以被看做是一个N*M的矩形方阵，其中左上角坐标为(1,1)，右下角坐标为(n,m)，每个格子(i,j)都有一个高度h(i,j)。
②洪水送(r,c)开始，如果一个格子被洪水淹没，那这个格子四周比它低（或相同）的格子也会被淹没。
现在松松想请你帮忙算算，有多少个格子不会被淹没，便于他和朋友逃脱。
【原有误数据已删除】
第一行包含两个整数n，m，表示矩形方阵右下角坐标。
以下n行，每行m个数，第i行第j个数表示格子(i,j)的高度。
最后一行包含两个整数r，c，表示最初被洪水淹没的格子。
输出仅一行，为永远不会被淹没的格子的数量。
3 3
1 2 3
2 3 4
3 4 5
2 2
5
对于90%的数据，保证随机生成。
对于100%的数据，1<=N,M<=1000。
题解：向四个方位漫搠，访问了就做标记
#include<bits/stdc++.h>
using namespace std;
int N,M;
int h[1005][1005],mp[1005][1005];
int f[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
void bfs(int r,int c){
mp[r][c]=1;
for(int i=0;i<4;i++){
int x=r+f[i][0];int y=c+f[i][1];
//cout<<x<<" "<<y<<" "<<h[x][y]<<"B"<<endl;
if(x>=1&&x<=N&&y>=1&&y<=M){
if(mp[x][y])continue;
if(h[x][y]<=h[r][c]){
bfs(x,y);
}
}
}
}
int main(){
int r,t,cnt=0;
cin>>N>>M;
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)scanf("%d",&h[i][j]);
scanf("%d%d",&r,&t);
bfs(r,t);
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
if(mp[i][j]==0)cnt++;
printf("%d\n",cnt);
}
浙公网安备 33010602011771号