2021/09/08_基础树图例题练习(1)
2021/09/08_基础树图例题练习(1)
2021/09/06 A.M. 7:40-10:40
| Problems | Hospital | Castle | City | Repair | Trade | Price | Tree | Drop |
| 预估分数 | 100 | 100 | 100 | 100 | 100 | 0 | 0 | 100 |
| 实际分数 | 100 | 100 | 100 | 100 | 100 | 0 | 0 | 100 |
解题报告
A:Hospital_医院设置
给出的题解描述的很简单:
“这是一道简单的二叉树应用问题,问题中的结点数并不多,数据规模也不大,采用邻接矩阵存储,用Floyed算法求出任意两结点之间的最短路径,然后穷举医院可能建立的n个结点位置,找出一个最小距离的位置即可。也可以用双链表结构 或带父结点信息的数组存储结构来解决。”
Floyd算法的时间复杂度为O(n^3),同时本题还要穷举可能建立医院的n的位置,总时间复杂度为O(n^4),还不如直接来一遍纯暴力痛快。
暴力枚举每个可能建立医院的位置,遍历图,求其“距离和”。取所有距离和的最小值即可。时间复杂度为O(n^2)。
B:Castle_黑暗城堡

题目描述 知道黑暗城堡有 N 个房间,M 条可以制造的双向通道,以及每条通道的长度。 城堡是树形的并且满足下面的条件: 设 Di为如果所有的通道都被修建,第 i 号房间与第 1 号房间的最短路径长度; 而 Si 为实际修建的树形城堡中第 i 号房间与第 1 号房间的路径长度; 要求对于所有整数 i(1≤i≤N),有 Si=Di 成立。 你想知道有多少种不同的城堡修建方案。当然,你只需要输出答案对 231−1 取模之后的结果就行了。 输入 第一行为两个由空格隔开的整数 N,M; 第二行到第 M+1 行为 3 个由空格隔开的整数 x,y,l:表示 x 号房间与 y 号房间之间的通道长度为 l。 输出 一个整数:不同的城堡修建方案数对 231−1 取模之后的结果。 样例输入 4 6 1 2 1 1 3 2 1 4 3 2 3 1 2 4 2 3 4 1 样例输出 6
这是题意简化后的题面了,开门见山,很直接。
最小生成树和最短路结合的板题。
先用Dijkstra算法求出1号房间到每个房间的单源最短路。此时以1为树形城堡的根。容易想到:若x是y的父节点,x,y之间的通道长度为z,则有:
dist[y]=dist[x]+z;
即题中的要求的树结构是最短路径生成树。满足任意一对父子节点x,y都有上式成立的树结构为图的一棵最短路径生成树。
接着,把所有节点按照dist的值升序排序,依次考虑把每个节点p加入树形城堡中有多少种方法。维护这棵最小路径生成树T,统计有多少个节点x满足x∈T满足上式。让p与其中任意一个x相连,都符合题意。
由乘法原理,每步统计的数量相乘得到答案。

#include<stdio.h> #include<string.h> #include<iostream> using namespace std; #define LL long long const int N=1010; const LL P=(1LL<<31)-1; int n,m,a[N][N],d[N]; LL ans=1; bool v[N]; int main(){ scanf("%d%d",&n,&m); memset(a,0x3f,sizeof(a)); for(int i=1;i<=n;++i)a[i][i]=0; for(int i=1;i<=m;++i){ int u,v,val; scanf("%d%d%d",&u,&v,&val); a[u][v]=a[v][u]=min(a[u][v],val); } memset(d,0x3f,sizeof(d)); d[1]=0; for(int i=1;i<n;++i){ int t=0; for(int j=1;j<=n;++j) if(!v[j]&&(!t||d[j]<d[t]))t=j; v[t]=1; for(int j=1;j<=n;++j) d[j]=min(d[j],d[t]+a[t][j]); } memset(v,0,sizeof(v)); v[1]=1; for(int i=1;i<n;++i){ int t=0,k=0; for(int j=2;j<=n;++j) if(!v[j]&&(!t||d[j]<d[t]))t=j; for(int j=1;j<=n;++j) if(v[j]&&d[j]+a[j][t]==d[t])++k; v[t]=1; (ans*=k)%=P; } printf("%lld",ans); }
C:City_繁忙的都市

题目描述 城市C是一个非常繁忙的大都市,城市中的道路十分的拥挤,于是市长决定对其中的道路进行改造。城市C的道路是这样分布的:城市中有n个交叉路口,有些交叉路口之间有道路相连,两个交叉路口之间最多有一条道路相连接。这些道路是双向的,且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值,分值越小表示这个道路越繁忙,越需要进行改造。但是市政府的资金有限,市长希望进行改造的道路越少越好,于是他提出下面的要求: 1.改造的那些道路能够把所有的交叉路口直接或间接的连通起来。 2.在满足要求1的情况下,改造的道路尽量少。 3.在满足要求1、2的情况下,改造的那些道路中分值最大的道路分值尽量小。 任务:作为市规划局的你,应当作出最佳的决策,选择那些道路应当被修建。 输入格式 第一行有两个整数n,m表示城市有n个交叉路口,m条道路。 接下来m行是对每条道路的描述,u, v, c表示交叉路口u和v之间有道路相连,分值为c。(1≤n≤300,1≤c≤10000,1≤m≤100000) 输出格式 两个整数s, max,表示你选出了几条道路,分值最大的那条道路的分值是多少。 输入输出样例 输入 4 5 1 2 3 1 4 5 2 4 7 2 3 6 3 4 8 输出 3 6
最小生成树的板题。很显然,就是求最大边权最小的生成树。
直接用kruskal算法。以边权为关键字,对边升序排序。关键在并查集操作,查找两点是否在一个生成树中。
此处不再赘述了。

#include<stdio.h> #include<algorithm> using namespace std; struct nm{ int x,y,z; }a[45054]; bool cmp(nm a,nm b){ return a.z<b.z; } int n,m,ans,sum; int fa[45054]; int Get(int x){ if(fa[x]==x)return x; return fa[x]=Get(fa[x]); } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=m;i++) scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z); sort(a+1,a+1+m,cmp); for(int i=1;i<=m;++i){ int u=a[i].x,v=a[i].y; int fx=Get(u),fy=Get(v); if(fx==fy) continue; ans=max(ans,a[i].z); fa[fy]=fx,sum++; } printf("%d %d",sum,ans); }
D:Repair_走廊泼水节

题目描述 我们一共有N个OIER打算参加这个泼水节,同时很凑巧的是正好有N个水龙头(至于为什么,我不解释)。N个水龙头之间正好有N-1条小道,并且每个水龙头都可以经过小道到达其他水龙头(这是一棵树,你应该懂的..)。但是OIER门为了迎接中中的挑战,决定修建一些个道路(至于怎么修,秘密~),使得每个水龙头到每个水龙头之间都有一条直接的道路连接(也就是构成一个完全图呗~)。但是OIER门很懒得,并且记性也不好,他们只会去走那N-1条小道,并且希望所有水龙头之间修建的道路,都要大于两个水龙头之前连接的所有小道(小道当然要是最短的了)。所以神COW们,帮那些OIER们计算一下吧,修建的那些道路总长度最短是多少,毕竟修建道路是要破费的~~ 输入 本题为多组数据~ 第一行t,表示有t组测试数据 对于每组数据 第一行N,表示水龙头的个数(当然也是OIER的个数); 2到N行,每行三个整数X,Y,Z;表示水龙头X和水龙头Y有一条长度为Z的小道 输出 对于每组数据,输出一个整数,表示修建的所有道路总长度的最短值。 样例输入 2 3 1 2 2 1 3 3 4 1 2 3 2 3 4 3 4 5 样例输出 4 17 数据范围与约定 每个测试点最多10组测试数据 50% n<=1500; 100% n<=6000 100% z<=100
题意简化之后如下:
给定一棵N个节点的树,要求增加若干条边,把这棵树扩充为完全图,并满足图的唯一最小生成树仍然是这棵树。求增加的边的权值总和最小是多少。
类比Kruskal算法,用并查集记录点之间的连通情况。
对于每次合并时,集合Sx与集合Sy之间一共会增加|Sx|*|Sy|条边,故将(z+1)*(|Sx|*|Sy|)累加至答案中。
算法时间复杂度为O(N*log(N))。

#include<stdio.h> #include<algorithm> using namespace std; struct rec{ int x,y,z; }edge[6010]; int fa[6010],s[6010],n,T; long long ans; bool operator<(rec a,rec b){ return a.z<b.z; } int get(int x){ if(x==fa[x])return x; return fa[x]=get(fa[x]); } int main(){ scanf("%d",&T); while(T--){ scanf("%d",&n); for(int i=1;i<n;i++) scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z); sort(edge+1,edge+n); for(int i=1;i<=n;i++) fa[i]=i,s[i]=1; ans=0; for(int i=1;i<n;i++){ int x=get(edge[i].x); int y=get(edge[i].y); if(x==y)continue; ans+=(long long)(edge[i].z+1)*(s[x]*s[y]-1); fa[x]=y; s[y]+=s[x]; } printf("%lld\n",ans); } }
E:Trade_最优贸易
NOIp原题。因为不会写强联通分量缩点加拓补序DP,果断最短路(w)。
分正反两图两次SPFA解决。

#include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int N=1e5+6,M=1e6+6; int n,m,tot,Price[N],Ans; int Head[N],Side[M],Next[M],ans[N]; int fHead[N],fSide[M],fNext[M],fans[N]; priority_queue<pair <int,int> >q; priority_queue<pair <int,int> >fq; void Addin(){ for(int i=1;i<=m;i++){ int x,y,z; scanf("%d%d%d",&x,&y,&z); Side[++tot]=y; Next[tot]=Head[x]; Head[x]=tot; fSide[tot]=x; fNext[tot]=fHead[y]; fHead[y]=tot; if(z==2){ Side[++tot]=x; Next[tot]=Head[y]; Head[y]=tot; fSide[tot]=y; fNext[tot]=fHead[x]; fHead[x]=tot; } } } void SP1(){ memset(ans,0x3f,sizeof(ans)); ans[1]=Price[1]; q.push(make_pair(-ans[1],1)); while(q.size()){ int x=q.top().second; q.pop(); for(int i=Head[x];i;i=Next[i]){ int y=Side[i]; if(ans[y] > ans[x]){ ans[y]=ans[x]; ans[y]=min(ans[y],Price[y]); q.push(make_pair(-ans[y],y)); } } } } void SP2(){ memset(fans,0xcf,sizeof(fans)); fans[n]=Price[n]; fq.push(make_pair(fans[n],n)); while(fq.size()){ int x=fq.top().second; fq.pop(); for(int i=fHead[x];i;i=fNext[i]){ int y=fSide[i]; if(fans[y]<fans[x]){ fans[y]=fans[x]; fans[y]=max(fans[y],Price[y]); fq.push(make_pair(fans[y],y)); } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&Price[i]); Addin(); SP1(); SP2(); for(int i=1;i<=n;i++) Ans=max(Ans,fans[i]-ans[i]); printf("%d",Ans); }
但是看到洛谷题解有直接用暴力DP过的,虽然好多人在下面说数据水,但反正是我想不到的方法了(w)。
E:Price_奖金

题目描述 由于无敌的凡凡在2005年世界英俊帅气男总决选中胜出,Yali Company总经理Mr. Z心情好,决定给每位员工发奖金。公司决定以每个人本年在公司的贡献为标准来计算他们得到奖金的多少。 于是Mr.Z下令召开m方会谈。每位参加会谈的代表提出了自己的意见:“我认为员工a的奖金应该比b高!”Mr.Z决定要找出一种奖金方案,满足各位代表的意见,且同时使得总奖金数最少。每位员工奖金最少为100元。 输入 第1行两个整数n、m,表示员工总数和代表数; 以下m行,每行2个整数a、b,表示某个代表认为第a号员工奖金应该比第b号员工高。 输出 若无法找到合理方案,则输出“Poor Xed”;否则输出一个数表示最少总奖金。 样例输入 2 1 1 2 样例输出 201 数据范围 80%的数据满足:n<= 1000,m<= 2000; 100%的数据满足:n< = 10000,m< =20000。
简单的拓补排序。但蒟蒻我根本没想到,好久没写过拓补排序了完全懵。回忆一下便好了。
按M个代表的意见建图,若图中有环则无解,否则拓扑排序之后算出总奖金。

#include<queue> #include<vector> #include<stdio.h> #include<string.h> using namespace std; const int Size=20005; int n,m; vector<int>p[Size]; int pay[Size]; int indeg[Size]; bool topsort(){ queue<int>Q; for(int i=1;i<=n;i++) if(!indeg[i])Q.push(i); int num=0; while(!Q.empty()){ int u=Q.front(); Q.pop(); num++; for(int i=0;i<p[u].size();i++){ if(--indeg[p[u][i]]==0) Q.push(p[u][i]); pay[p[u][i]]=max(pay[u]+1,pay[p[u][i]]); } } if(n==num)return 1; return 0; } int main(){ scanf("%d %d",&n,&m); for(int i=1;i<=n;i++) pay[i]=100; memset(indeg,0,sizeof(indeg)); int x,y; for(int i=0;i<m;i++){ scanf("%d %d",&x,&y); p[y].push_back(x); indeg[x]++; } int sum=0; if(topsort()){ for(int i=1;i<=n;i++) sum+=pay[i]; printf("%d\n",sum); }else printf("Poor Xed\n"); }
F:Tree_对称二叉树

题目描述 如果二叉树的左右子树的结构是对称的,即两棵子树皆为空,或者皆不空,则称该二叉树是对称的。编程判断给定的二叉树是否对称。 输入 二叉树用顺序结构给出,若读到#则为空,二叉树 T1=ABCDE,T2=ABCD#E. 输出 如果二叉树是对称的,输出“Yes”,反之输出“No”。 样例输入1 ABCDE 样例输出1 Yes 样例输入2 ABCD#E 样例输出2 No
之前做了几道二叉树难题(对我这种蒟蒻),看到二叉树直接跳过了。然而就是一道很基础的二叉树的题。想了几分钟就知道怎么做了。
由于本题的二叉树是满二叉树,并且是按深度从左至右依次输出的,所以直接判断就可以了。

#include<stdio.h> #include<string.h> int main(){ char s[1001]; scanf("%s",s); int len=strlen(s),i; for(i=1;i<len;i+=2) if((s[i]!='#'&&s[i+1]=='#')||(s[i+1]!='#'&&s[i]=='#')||s[i+1]=='\0'){ printf("No"); break; } if(i>=len)printf("Yes"); }
E:Drop_小球

题目描述 许多的小球一个一个的从一棵满二叉树上掉下来组成 FBT(Full Binary Tree,满二叉树),每一时间,一个正在下降的球第一个访问的是非叶子节点。然后继续下降时,或者走右子树,或者走左子树,直到访问到叶子节点。决定球运动方向的是每个节点的布尔值。最初,所有的节点都是 false,当访问到一个节点时,如果这个节点是 false,则这个球把它变成 true,然后从左子树走,继续它的旅程。如果节点是 true,则球也会改变它为 false,而接下来从右子树走。满二叉树的标记方法如下图。 因为所有的节点最初为 false,所以第一个球将会访问节点 1,节点 2 和节点 4,转变节点的布尔值后在在节点 8 停止。第二个球将会访问节点 1、3、6,在节点 12 停止。明显地,第三个球在它停止之前,会访问节点 1、2、5,在节点 10 停止。 现在你的任务是,给定 FBT 的深度 D,和 I,表示第 I 个小球下落,你可以假定 I 不超过给定的 FBT 的叶子数,写一个程序求小球停止时的叶子序号。 输入 仅一行包含两个用空格隔开的整数 D 和 I。其中 2<=D<=20,1<=I<=524288。 输出 对应输出第 I 个小球下落停止时的叶子序号。 样例输入 4 2 样例输出 12
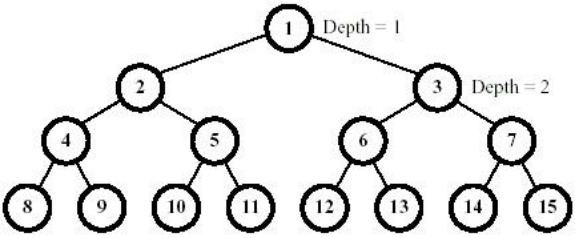
看到图感觉和线段树的标点方法有异曲同工之妙。
直接上暴力啦。暴力使我快乐。

#include<stdio.h> int d,l; int a[1<<21]; int main(){ scanf("%d%d",&d,&l); for(int i=1;i<=l;++i){ int pos=1; while(pos<(1<<d)){ if(pos<(1<<(d-1))){ if(!a[pos])a[pos]^=1,pos<<=1; else a[pos]^=1,pos=(pos<<1)+1; } if(pos>=(1<<(d-1))&&pos<=(1<<d)-1){ a[pos]=i; break; } } if(i==l)return(printf("%d",pos)&&0); } }
最后安利一首春泥棒-ヨルシカ
(尝试夹带私货啊哈哈哈)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号