YbtOJ 「图论」第2章最小生成树

最小生成树kruskal(无向图)

求一张图中边权最小且包含所有点的树将每一条边记录到结构体中再将所有边按照边权排序从小到大加边用并查集维护节点之间的关系如果遍历到当前这条边的两个节点在同一个集合内就舍弃这条边去找下一条小边

struct node
{
	int u , v , w;
	bool operator < ( const node &a ) const { return w < a.w; }
}a[N];
int find ( int x )
{
	if ( fa[x] == x ) return x;
	else return fa[x] = find ( fa[x] );
}
for ( int i = 1 ; i <= n ; i ++ ) fa[i]= i;
sort ( a + 1 , a + m + 1 );
for ( int i = 1 ; i <= m ; i ++ )
{
	int fu = find ( a[i].u ) , fv = find ( a[i].v );
	if ( fu != fv )
	{
		fa[fu] = fv;
		ans += a[i].w;
	}
}

A. 【例题1】繁忙都市

[题目描述]

城市 C 是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。城市 C 的道路是这样分布的：城市中有 \(n\) 个交叉路口，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连接。这些道路是双向的，且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值，分值越小表示这个道路越繁忙，越需要进行改造。但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的要求：

改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
在满足要求 1 的情况下，改造的道路尽量少。
在满足要求 1、2 的情况下，改造的那些道路中分值最大的道路分值尽量小。

任务：作为市规划局的你，应当作出最佳的决策，选择哪些道路应当被修建。

[输入格式]

第一行有两个整数 \(n,m\) 表示城市有 \(n\) 个交叉路口，\(m\) 条道路。

接下来 \(m\) 行是对每条道路的描述，\(u, v, c\) 表示交叉路口 \(u\) 和 \(v\) 之间有道路相连，分值为 \(c\)。

[输出格式]

两个整数 \(s, \mathit{max}\)，表示你选出了几条道路，分值最大的那条道路的分值是多少。

[算法分析]

裸题

[代码实现]

#include <bits/stdc++.h>

using namespace std;

#define inl inline

const int N = 1e5 + 5;



inl int read ()

{

	int x = 0 , f = 1;

	char ch = getchar();

	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }

	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }

	return x * f;

} 



int fa[N] , maxx , n , m;

struct node

{

	int u , v , w;

	bool operator < ( const node &a ) const { return w < a.w; }

}a[N];


int find ( int x )

{

	if ( fa[x] == x ) return x;

	else return fa[x] = find ( fa[x] );

}





int main()

{

	n = read() , m = read();

	for ( int i = 1 ; i <= m ; i ++ ) a[i].u = read() , a[i].v = read() , a[i].w = read();

	for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i;

	sort ( a + 1 , a + m + 1 );

	for ( int i = 1 ; i <= m ; i ++ )

	{

		int fu = find ( a[i].u ) , fv = find ( a[i].v );

		if ( fu != fv )

		{

			fa[fu] = fv;

			maxx = a[i].w;

		}

	}

	printf ( "%d %d" , n - 1 , maxx );

	return 0;	

}

B. 【例题2】新的开始

[题目描述]

Farmer John 的农场缺水了。

他决定将水引入到他的 \(n\) 个牧场。他准备通过挖若干井，并在各块田中修筑水道来连通各块田地以供水。在第 \(i\) 号田中挖一口井需要花费 \(W_i\) 元。连接 \(i\) 号田与 \(j\) 号田需要 \(P_{i,j}\)（\(P_{j,i}=P_{i,j}\)）元。

请求出 FJ 需要为使所有农场都与有水的农场相连或拥有水井所需要的最少钱数。

[输入格式]

第一行为一个整数 \(n\)。

接下来 \(n\) 行，每行一个整数 \(W_i\)。

接下来 \(n\) 行，每行 \(n\) 个整数，第 \(i\) 行的第 \(j\) 个数表示连接 \(i\) 号田和 \(j\) 号田需要的费用 \(P_{i,j}\)。

[输出格式]

输出最小开销。

[算法分析]

我们将\(0\)节点想象成水源点每一个村庄必须间接或直接地与水源点连接

建边的时候除了题目中给定的边之外 \(0\)节点还需要向每一个村庄连\(w\)权边之后跑最小生成树即可

[代码实现]

#include <bits/stdc++.h>
using namespace std;
#define inl inline

const int N = 1e5 + 5;

inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
} 

int fa[N] , ans , n;
struct node
{
	int u , v , w;
}e[N];




int find ( int x )
{
	if ( fa[x] == x ) return x;
	else return fa[x] = find ( fa[x] );
}


int main()
{
	n = read();
	for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i;
	for ( int i = 1 ; i <= n ; i ++ ) e[i].u = 0 , e[i].v = i , e[i].w = read();
	int l = n;
	for ( int i = 1 ; i <= n ; i ++ )
		for ( int j = 1 ; j <= n ; j ++ )
		{
			int temp = read();
			if ( i < j ) e[++l] = { i , j , temp };
		}
	sort ( e + 1 , e + l + 1 , [](const node &a , const node &b) { return a.w < b.w; } );
	for ( int i = 1 ; i <= l ; i ++ )
	{
		int fu = find(e[i].u) , fv = find(e[i].v);
		if ( fu != fv )
		{
			fa[fu] = fv;
			ans += e[i].w;
		}
	}
	printf ( "%d" , ans );
	return 0;	
}

C. 【例题3】公路建设

[题目描述]

A国是一个新兴的国家，有\(n\)个城市，编号\(1-n\) 政府想大搞公路建设，提供了优惠政策：对于每一个投资方案的预计总费用，政府负担\(50\%\)费用

世界各地的大公司纷纷投资，并提出了自己的建设方案，他们的投资方案包括这些内容：公路连接的两座城市的编号，预计的总费用(假设他们的预计总是准确的)。

你作为A国公路规划局的总工程师，有权力决定每一个方案是否接受。但是政府给你的要求是：

要保证各个城市之间都有公路直接或间接相连。
因为是新兴国家，政府的经济实力还不强。政府希望负担最少的费用。
因为大公司并不是同时提出方案，政府希望每接到一个方案，就可以知道当前需要负担的最小费用和接受的投资方案，以便随时开工。关于你给投资公司的回复可以等到开工以后再给。

注意：A国一开始是没有公路的。

[输入格式]

第\(1\)行有两个数字\(n,m\)

第\(2\)行到第\(n+1\)行给出了各个投资方案，第\(i\)行的方案编号为\(i-1\)，编号小的方案先接到，一个方案占一行，每行有\(3\)个数字，分别是连接的两个城市编号\(a\)、\(b\)和投资的预计总费用\(w\)。

[输出格式]

输出文件共有\(m\)行。每一行的第一个数字是当前政府需要负担的最少费用(保留\(1\)位小数)，但如果此时接受的所有投资方案不能保证政府的第一条要求，那么这一行只有一个数字\(0\)。

[算法分析]

暴力跑\(m\)次最小生成树可以优化每一次的排序复杂度因为每一次只会加入一个值所有\(O(n)\)插入即可

[代码实现]

#include <bits/stdc++.h>
using namespace std;
#define inl inline

const int N = 1e5 + 5;

inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
} 

int fa[N] , cnt , ans , n , m;
struct node
{
	int u , v , w;
	bool operator < ( const node &a ) const { return w < a.w; }
}e[N];
int find ( int x )
{
	if ( fa[x] == x ) return x;
	else return fa[x] = find ( fa[x] );
}


int main()
{
	n = read() , m = read();
	for ( int l = 1 ; l <= m ; l ++ )
	{
		e[l].u = read() , e[l].v = read() , e[l].w = read();
		for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i;
		for ( int i = l ; i ; i -- )//将新加入的这个值塞入到有序数列的对应位置中 用sort也行 但是更慢
		{
			if ( e[i].w < e[i-1].w ) swap ( e[i] , e[i-1] );
			else break;
		}
		cnt = 0 , ans = 0;
		for ( int i = 1 ; i <= l ; i ++ )
		{
			int fu = find(e[i].u) , fv = find(e[i].v);
			if ( fu != fv )
			{
				fa[fu] = fv;
				ans += e[i].w;
				cnt ++;
			}
			if ( cnt == n - 1 ) break;
		}
		if ( cnt < n - 1 ) printf ( "0\n" );
		else printf ( "%.1lf\n" , ans * 1.0 / 2 * 1.0 );
	}

	return 0;	
}

D. 【例题4】构造完全图

[题目描述]

对于完全图\(G\)，若有且仅有一棵最小生成树\(T\)，则称完全图\(G\)是树\(T\)扩展出的。

给你一棵树\(T\)，找出\(T\)能扩展出的边权和最小的完全图。

[输入格式]

第一行正整数\(N\)表示树\(T\)的点数；

接下来\(n-1\)行三个整数\(u,v,w\)；描述一条边

保证输入数据构成一棵树。

[输出格式]

输出仅一个数，表示最小的完全图的边权和。

[算法分析]

类比最小生成树的原理先将所有给定的边来排序然后从小到大加入边对于每一条边将它两边集合之间需要连的边的边权都设置为\(w+1\)(当前这一条边除外)

如果不排序会导致出错因为可能在以前加边的时候在这两个点之间加入了其他小边不能保证两个点之间的最小边是这个大边

[代码实现]

#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int N = 1e5 + 5;

inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
} 

int fa[N] , sz[N] , ans , n;
struct node
{
	int u , v , w;
	bool operator < ( const node &a ) const { return w < a.w; }
}e[N];
int find ( int x )
{
	if ( fa[x] == x ) return x;
	else return fa[x] = find ( fa[x] );
}


signed main()
{
	n = read();
	for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i , sz[i] = 1;
	for ( int i = 1 ; i < n ; i ++ ) e[i].u = read() , e[i].v = read() , e[i].w = read();
	sort ( e + 1 , e + n , [](const node a , const node b) { return a.w < b.w; } );
	for ( int i = 1 ; i <= n - 1 ; i ++ )
	{
		int fu = find(e[i].u) , fv = find(e[i].v);
		if ( fu != fv )
		{
			ans += ( sz[fu] * sz[fv] ) * ( e[i].w + 1 ) - 1;
			sz[fu] += sz[fv];
			fa[fv] = fu;
		}
	}
	printf ( "%lld" , ans );
	return 0;	
}

E. 1.连接云朵

裸题

#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int N = 1e6 + 5; 
inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
}

int fa[N] , n , m , k;

struct node { int u , v , w; } e[N];

int find ( int x )
{
	if ( fa[x] == x ) return x;
	else return fa[x] = find(fa[x]);
}

signed main ()
{
	n = read() , m = read() , k = read();
	for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i;
	for ( int i = 1 ; i <= m ; i ++ ) e[i].u = read() , e[i].v = read() , e[i].w = read(); 
	sort ( e + 1 , e + m + 1 , [](const node &a , const node &b) { return a.w < b.w; } );
	for ( int i = 1 , ans = n  , res = 0 ; i <= m ; i ++ )
	{
		int fu = find(e[i].u) , fv = find(e[i].v);
		if ( fu == fv ) continue;
		fa[fu] = fv;
		ans --;
		res += e[i].w;
		if ( ans == k ) { cout << res << endl; return 0; }
	}
	cout << "No Answer" << endl;
	return 0;
}

F. 2.序列破解

[题目描述]

魔术师的桌子上有 \(n\) 个杯子排成一行，编号为 \(1,2,…,n\)，其中某些杯子底下藏有一个小球，如果你准确地猜出是哪些杯子，你就可以获得奖品。

花费 \(c_{ij}\) 元，魔术师就会告诉你杯子 \(i,i+1,…,j\) 底下藏有球的总数的奇偶性。

采取最优的询问策略，你至少需要花费多少元，才能保证猜出哪些杯子底下藏着球？

[输入格式]

第一行一个整数 \(n\)。

第 \(i+1\) 行（\(1\le i\le n\)）有 \(n+1-i\) 个整数，表示每一种询问所需的花费。

其中 \(c_{ij}\)（对区间 \([i,j]\) 进行询问的费用，\(1\le i\le j\le n\)）为第 \(i+1\) 行第 \(j+1-i\) 个数。

[输出格式]

输出一个整数，表示最少花费。

[算法分析]

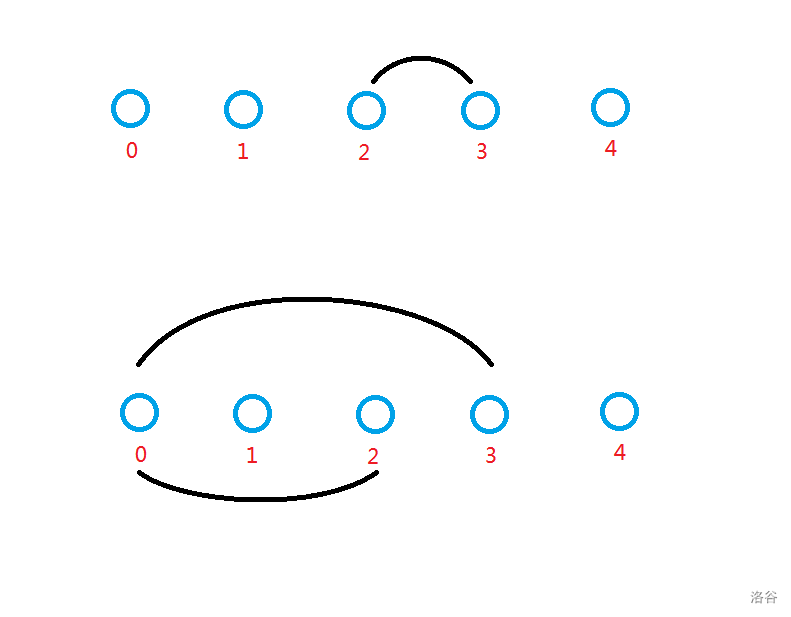
神题举例说明:

我们想得到3这个位置的奇偶性那么有两种方法:

直接查询\(3,3\)
查询\(1\)到\(2\),\(1\)到\(3\)的值

所以当我们知道\([l,r1]\)和区间\([l,r2]\)的奇偶性之后我们就可以知道区间\([r1+1,r2]\)的奇偶性

考虑将\(n\)个杯子看作\(n\)个点将知道\([l,r]\)的奇偶性看成是\(l\)向\(r\)连边这样如果有边\([l,r1]\)和边\([l,r2]\)就相当于图中有边\([r1+1,r2]\)

但是这条性质并不能搞出连通性所以考虑换边的定义 知道\([l,r]\)的奇偶性看作是\(l-1\)向\(r\)连边 这样如果有边\([l,r1]\)和边\([l,r2]\)就相当于图中有边\([r1,r2]\)

那么我们如果想要知道所有点的奇偶性那么我们需要将所有相邻的点都相连也就是说这张图是连通的最后跑最小生成树即可

边数组需要开大一点()

[代码实现]

#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int N = 1e6 + 5; 
inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
}

int fa[N] , n , m;

struct node { int u , v , w; } e[50000000];

int find ( int x )
{
	if ( fa[x] == x ) return x;
	else return fa[x] = find(fa[x]);
}

signed main ()
{
	n = read();
	for ( int i = 0 ; i <= n ; i ++ ) fa[i] = i;
	for ( int i = 1 ; i <= n ; i ++ )
		for ( int j = i ; j <= n ; j ++ )
			e[++m] = { i - 1 , j , read() };
	sort ( e + 1 , e + m + 1 , [](const node &a , const node &b) { return a.w < b.w; } );
	int ans = 0;
	for ( int i = 1 ; i <= m ; i ++ ) 
	{
		int fu = find(e[i].u) , fv = find(e[i].v);
		if ( fu == fv ) continue;
		fa[fu] = fv;
		ans += e[i].w;
	}
	cout << ans << endl;
	return 0;	
}

G. 3.生物进化

我们将所有可能的关系连边跑最小生成树将生成树中的边记录下来再用dfs搜索一遍判断父亲

#include <bits/stdc++.h>
using namespace std;
#define inl inline

const int N = 1e7 + 5; 
inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
}
		
int fa[N] , n , tot;
		
int find ( int x )
{
	if ( x == fa[x] ) return x;
	return fa[x] = find(fa[x]);
}
		
		
int head[N] , cnt;
struct node { int to , nxt; } e[N];
void add ( int u , int v ) { e[++cnt] = { v , head[u] } , head[u] = cnt; }
		
struct edge { int u , v , w; } a[N];
		
void dfs ( int u , int ff )
{
	fa[u] = ff;
	for ( int i = head[u] ; i ; i = e[i].nxt )
		if ( e[i].to != ff ) dfs ( e[i].to , u );
}
		
signed main ()
{
	n = read();
	for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i;
	for ( int i = 1 ; i <= n ; i ++ ) 
		for ( int j = 1 , w ; j <= n ; j ++ )
			w = read() , a[++tot] = { i , j , w };
	sort ( a + 1 , a + tot + 1 , [](const edge &a , const edge &b) { return a.w < b.w; } );
	for ( int i = 1 ; i <= tot ; i ++ )
	{
		int fu = find(a[i].u) , fv = find(a[i].v);
		if ( fu == fv ) continue;
		fa[fu] = fv;
		add ( a[i].u , a[i].v );
		add ( a[i].v , a[i].u );
	}
	dfs ( 1 , 0 );
	for ( int i = 2 ; i <= n ; i ++ ) cout << fa[i] << endl;
	return 0;
}

H. 4.保留道路

\(50pts\):类比公路建设每一次插入一条新边做一次最小生成树如果不能保证连通就继续加边否则统计答案复杂度\(O(M^2)\)

#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long 
const int N = 1e7 + 5; 
const int inf = 0x3f3f3f3f3f3f3f3f;
inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
}
		
int fa[N] , n , m , WS , wg , tot , ans = inf;

struct node { int u , v , g , s; } e[N];
		
int find ( int x )
{
	if ( x == fa[x] ) return x;
	return fa[x] = find(fa[x]);
}
		
signed main ()
{
	n = read() , m = read() , wg = read() , WS = read();
	for ( int i = 1 ; i <= m ; i ++ ) e[++tot].u = read() , e[tot].v = read() , e[tot].g = read() , e[tot].s = read();
	sort ( e + 1 , e + m + 1 , [](const node &a , const node &b) { return a.g < b.g; } );
	for ( int i = 1 ; i <= m ; i ++ )
	{
		for ( int j = 1 ; j <= n ; j ++ ) fa[j] = j;
		for ( int j = i ; j ; j -- )
		{
			if ( e[j].s < e[j-1].s ) swap ( e[j] , e[j-1] );
			else break;
		}
		int maxs = -inf , maxg = -inf , ct = 0;
		for ( int j = 1 ; j <= i ; j ++ )
		{
			int fu = find(e[j].u) , fv = find(e[j].v);
			if ( fu == fv ) continue;
			ct ++;
			fa[fu] = fv;
			maxs = max ( maxs , e[j].s );
			maxg = max ( maxg , e[j].g );
			if ( ct == n - 1 ) break;
		}
		if ( ct < n - 1 ) continue;
		ans = min ( ans , wg * maxg + WS * maxs );
	}
	if ( ans == inf ) cout << "-1" << endl;
	else cout << ans << endl;	
	return 0;
}

\(100pts\):我们按照\(g\)的顺序排序那么在不断加入新边的过程中当前的最小生成树只可能是由未加入新边的最小生成树边和当前新边组成的\(n\)条边中中选出来\(n-1\)条构成

因此维护一个最小生成树边集每一次只在\(n\)条边中做最小生成树

注意每次做最小生成树的时候需要同时更新边集

#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long 
const int N = 1e7 + 5; 
const int inf = 0x3f3f3f3f3f3f3f3f;
inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
}
		
int fa[N] , n , m , WS , wg , tot , ans = inf , top , j;

struct node { int u , v , g , s; } e[N] , sta[N];
		
int find ( int x )
{
	if ( x == fa[x] ) return x;
	return fa[x] = find(fa[x]);
}
		
signed main ()
{
	n = read() , m = read() , wg = read() , WS = read();
	for ( int i = 1 ; i <= m ; i ++ ) e[++tot].u = read() , e[tot].v = read() , e[tot].g = read() , e[tot].s = read();
	sort ( e + 1 , e + m + 1 , [](const node &a , const node &b) { return a.g < b.g; } );
	for ( int i = 1 ; i <= m ; i ++ )
	{
		for ( j = 1 ; j <= n ; j ++ ) fa[j] = j;
		sta[++top] = e[i];
		for ( j = top ; j ; j -- )
		{
			if ( sta[j-1].s > sta[j].s ) swap ( sta[j] , sta[j-1] ); 
			else break;
		}
		int ct = 0;
		for ( j = 1 ; j <= top ; j ++ )
		{
			int fu = find(sta[j].u) , fv = find(sta[j].v);
			if ( fu == fv ) continue;
			fa[fu] = fv;
			sta[++ct] = sta[j];
			if ( ct == n - 1 ) break;
		}
		if ( ct == n - 1 ) ans = min ( ans , wg * e[i].g + WS * sta[ct].s );
		top = ct;
	}
	if ( ans == inf ) cout << "-1" << endl;
	else cout << ans << endl;	
	return 0;
}

I. 5.最小距离和

方法1:循环两次对每个点两两建边边权为两点距离最后做最小生成树显然会爆炸

方法2:可以发现方法一建了很多无用的边我们考虑简化

如果是一维空间的话那么只有相邻的两个点可以被连边因为如果不相邻的两个点连边的话显然不如相邻连边优

那么推广到三维将边分别按照xyz坐标排序一次每次将相邻的点连边即可

#include <bits/stdc++.h>
using namespace std;
#define inl inline

const int N = 1e7 + 5; 
inl int read ()
{
	int x = 0 , f = 1;
	char ch = getchar();
	while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
	while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
	return x * f;
}

int fa[N] , n , cnt , ans;

struct node { int x , y , z , id; } a[N];
struct edge { int u , v , w; } e[N];

int find ( int x )
{
	if ( x == fa[x] ) return x;
	else return fa[x] = find(fa[x]);
}

signed main ()
{
	ios::sync_with_stdio(false);
	cin.tie(0) , cout.tie(0);
	n = read();
	for ( int i = 1 ; i <= n ; i ++ ) a[i].x = read() , a[i].y = read() , a[i].z = read() , a[i].id = i;
	for ( int i = 1 ; i <= n ; i ++ ) fa[i] = i;
	sort ( a + 1 , a + n + 1 , [](const node a , const node b) { return a.x < b.x; } );
	for ( int i = 1 ; i < n ; i ++ ) e[++cnt] = { a[i].id , a[i+1].id , a[i+1].x - a[i].x };
	sort ( a + 1 , a + n + 1 , [](const node a , const node b) { return a.y < b.y; } );
	for ( int i = 1 ; i < n ; i ++ ) e[++cnt] = { a[i].id , a[i+1].id , a[i+1].y - a[i].y };
	sort ( a + 1 , a + n + 1 , [](const node a , const node b) { return a.z < b.z; } );
	for ( int i = 1 ; i < n ; i ++ ) e[++cnt] = { a[i].id , a[i+1].id , a[i+1].z - a[i].z };
	sort ( e + 1 , e + cnt + 1 , [](const edge a , const edge b) { return a.w < b.w; } );
	for ( int i = 1 ; i <= cnt ; i ++ )
	{
		int fu = find(e[i].u) , fv = find(e[i].v);
		if ( fu == fv ) continue;
		fa[fu] = fv; ans += e[i].w;
	}
	cout << ans << endl;
	return 0;
}

posted @ 2023-06-25 09:41 Echo_Long 阅读(224) 评论(1) 收藏举报

刷新页面返回顶部

Echo-Long

YbtOJ 「图论」第2章最小生成树

最小生成树kruskal(无向图)

A. 【例题1】繁忙都市

B. 【例题2】新的开始

C. 【例题3】公路建设

D. 【例题4】构造完全图

E. 1.连接云朵

F. 2.序列破解

G. 3.生物进化

H. 4.保留道路

I. 5.最小距离和

公告