CF749B Parallelogram is Back 题解

Content

给出平行四边形的三个顶点 \((x_1,y_1),(x_2,y_2),(x_3,y_3)\)，求出所有可能的第四个顶点。

数据范围：\(\forall i\in[1,3],-1000\leqslant x_i,y_i\leqslant 1000\)。

Solution

这题可以通过平行四边形的一个性质轻松搞定——平行四边形的对角线互相平分。

啥啥啥？你还不知道什么是平行四边形？

因为太占空间，去这里看吧qwq。

那么用这个有什么用呢？

我们都知道，一条线段 \(AB\) 的中点计算公式是 \((\dfrac{x_A+x_B}{2},\dfrac{y_A+y_B}{2})\)，那么我们来看到下面这个平行四边形：

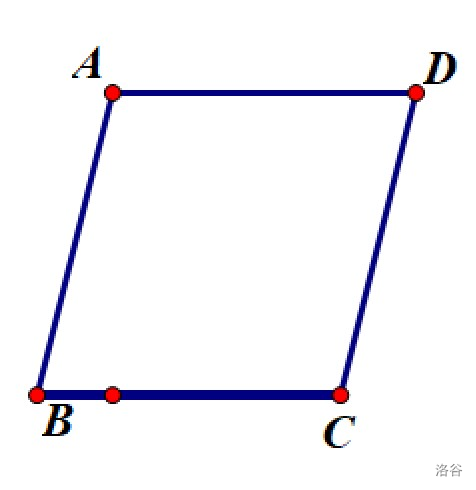
那么，我们通过上面这个平行四边形的性质可以得到，\(AC\) 和 \(BD\) 的中点是同一个点。那么我们就有：

\[\begin{cases}\dfrac{x_A+x_C}{2}=\dfrac{x_B+x_D}{2}&...(1)\\\dfrac{y_A+y_C}{2}=\dfrac{y_B+y_D}{2}&...(2)\end{cases} \]

将 \((1)\) 式和 \((2)\) 式分别都乘上 \(2\)可以得到：\(x_A+x_C=x_B+x_D,y_A+y_C=y_B=y_D\)。

所以，现在假设 \(A,B,C\) 三个点为题目中的已知点，那么第四个点 \(D\) 可以有以下几种：

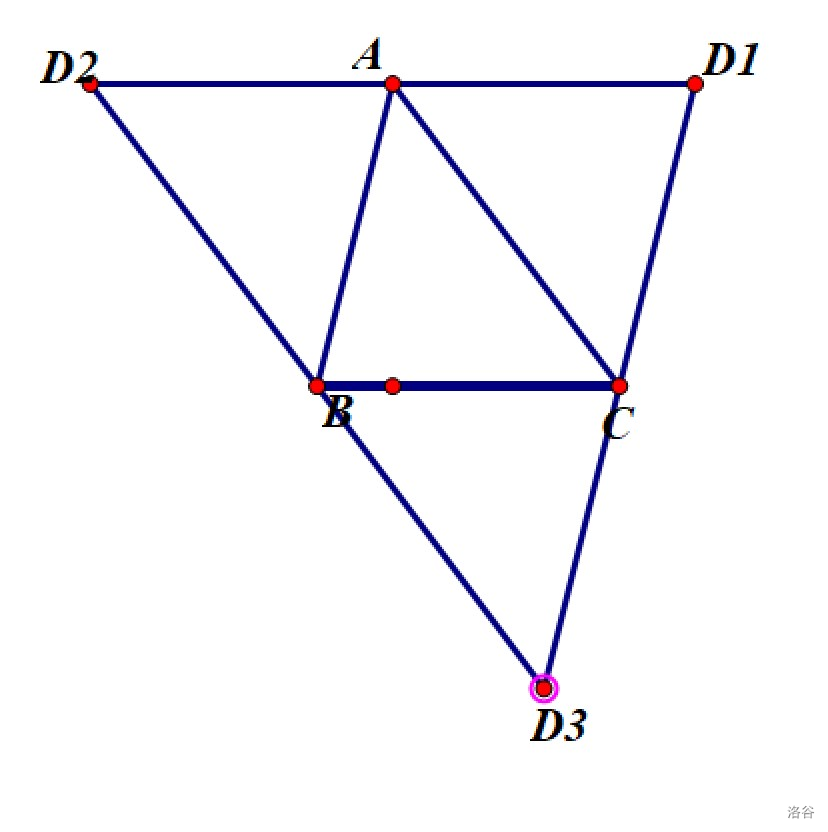
我们可以通过计算得到：

\(D_1(x_A+x_C-x_B,y_A+y_C-y_B)\)
\(D_2(x_A+x_B-x_C,y_A+y_B-y_C)\)
\(D_3(x_B+x_C-x_A,y_B+y_C-y_A)\)

我们可以发现，有且仅有以上这三个点符合要求。因此，满足点的个数为 \(3\)，坐标直接按照上面的公式输出即可（顺序可以任意）。

Code

#include <cstdio>
#include <algorithm>
#include <iostream>
using namespace std;

int x1, y1, x2, y2, x3, y3;

int main() {
	scanf("%d%d%d%d%d%d", &x1, &y1, &x2, &y2, &x3, &y3);
	printf("3\n%d %d\n%d %d\n%d %d", x2 + x3 - x1, y2 + y3 - y1, x1 + x3 - x2, y1 + y3 - y2, x1 + x2 - x3, y1 + y2 - y3);
}