LuoguP7043 「MCOI-03」村国 题解
Content
有 \(T\) 组询问,每组询问给定一个有 \(n\) 个节点的数,编号为 \(1\sim n\),每个节点一开始都有权值 \(a_i\)。现有 \(m\) 次操作,每次操作选择树上所有节点中权值最大的一个点(如果有多个选择编号最小的),然后将所有和这个点在树上直接相连的点的权值加 \(1\)。求 \(m\) 次操作以后权值最大的点的编号(如果有多个输出编号最小的)。
数据范围:\(1\leqslant n\leqslant 2\times 10^6,1\leqslant m\leqslant 10^{18},1\leqslant a_i\leqslant 2^{31}-1,1\leqslant T\leqslant 10\)。
Solution
比较具有启发性的题目。
我们先把 \(30\) 分的暴力(本人亲测)写完以后,看能不能找到一些规律。
我们接下来以这个图为例来找一下规律,下图是一个拥有 \(12\) 个节点的树,其中每个节点旁边红色的数字代表着它的权值。(图画得可能不是太好,请见谅)
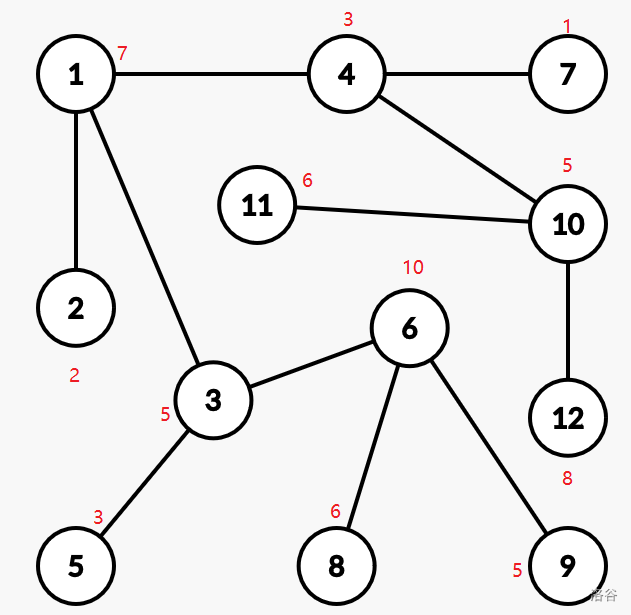
你也可以直接复制下面的对应数据来 \(\texttt{debug}\) 一下:
1
12 x //这里的 x 可以变成任何数
7 2 5 3 3 10 1 6 5 5 6 8
1 2
1 3
1 4
3 5
3 6
6 8
6 9
4 7
4 10
10 11
11 12
我们来模拟一下每次操作:
第一次,选择权值最大的节点 \(6\),然后让与之直接相连的每个节点的权值增加 \(1\),这样,与之直接相连的节点 \(3,8,9\) 的权值分别变成了 \(6,7,6\)。
第二次,第三次,第四次操作都是选择权值最大的节点 \(6\),就不再赘述了。第四次操作完成以后,节点 \(3,8,9\) 的权值分别变成了 \(9,10,9\)。
第五次,选择权值最大的节点,这是我们发现这样的节点有 \(2\) 个,分别是 \(6\) 和 \(8\),然而由于 \(6<8\),所以我们还是选择节点 \(6\),然后让与之直接相连的每个节点的权值增加 \(1\),这样,与之直接相连的节点 \(3,8,9\) 的权值分别变成了 \(10,11,10\)。
第六次,选择权值最大的节点 \(8\),然后让与之直接相连的每个节点的权值增加 \(1\),与之相连的节点 \(6\) 的权值变成了 \(11\)。
第七次,选择权值最大的节点,这是我们发现这样的节点有 \(2\) 个,分别是 \(6\) 和 \(8\),然而由于 \(6<8\),所以我们还是选择节点 \(6\),然后让与之直接相连的每个节点的权值增加 \(1\),这样,与之直接相连的节点 \(3,8,9\) 的权值分别变成了 \(11,12,11\)。
第八次,选择权值最大的节点 \(8\),然后让与之直接相连的每个节点的权值增加 \(1\),与之相连的节点 \(6\) 的权值变成了 \(12\)。
……
继续这样推下去的话你就能够发现,我们后面所选择的节点一定会在 \(6,8\) 之间反复循环,而这两个点又分别是一开始权值最大的点中编号最小的点和与之直接相连的节点中权值最大的点中编号最小的点。所以,我们可以得到以下思路:
- 记录下来所有与一开始权值最大的点中编号最小的点直接相连的所有点并取当中权值最大的点中编号最小的点。设我们选出来的点的编号分别是 \(k,k'\)。
- 如果 \(a_k-a_{k'}>m\),那么我们的节点 \(k\) 肯定是最后权值最大的点。
- 否则,由于最后的答案肯定在两个点之间反复横跳,我们只需要判断一下 \(m-(a_k-a_{k'})\) 的奇偶性即可。如果是奇数,那么答案肯定就是这两个点当中编号更大的,否则肯定就是这两个点当中编号更小的。这里请读者自己思考。
而且我们惊奇地发现,这个做法成功的越过了全网大部分人跳进去的 \(n=1\) 的坑,所以这个做法从某种意义上来讲是很优越的。
Code
int t, n, a[2000007], num[2000007];
long long m;
int main() {
//This program is written by Eason_AC
scanf("%d", &t);
while(t--) {
memset(num, 0, sizeof(num));
int ans = 0;
scanf("%d%lld", &n, &m);
for(int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
if((a[i] > a[ans]) || (a[i] == a[ans] && ans > i)) ans = i;
}
for(int i = 1; i < n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
if(x == ans) num[++num[0]] = y;
else if(y == ans) num[++num[0]] = x;
}
if(!num[0]) {printf("%d\n", ans); continue;}
int kk = 1;
for(int i = 1; i <= num[0]; ++i)
if(a[num[i]] > a[num[kk]]) kk = i;
if(a[ans] - a[num[kk]] > m) printf("%d\n", ans);
else if((m - (a[ans] - a[num[kk]])) % 2) printf("%d\n", max(num[kk], ans));
else printf("%d\n", min(num[kk], ans));
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号