LuoguB2030 计算线段长度 题解
Content
已知线段的两个端点的坐标 \(A(X_a,Y_a),B(X_b,Y_b)\) ,求线段 \(AB\) 的长度。
数据范围:\(|X_a|,|Y_a|,|X_b|,|Y_b|\leqslant 10000\)。
Solution
我们先给出平面直角坐标系上两点之间的距离公式:\(d_{AB}=\sqrt{(X_a-X_b)^2+(Y_a-Y_b)^2}\)。
那么我们怎么证?勾股定理。显然 \(A,B\) 的距离等于横坐标之差的平方加纵坐标之差的平方再开根号。不妨画个图理解一下:
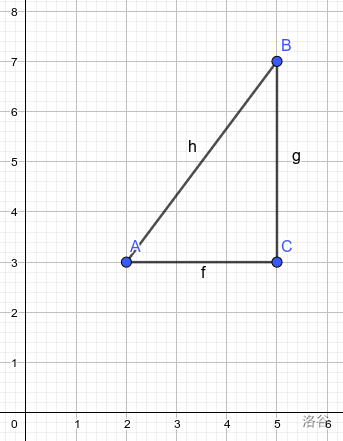
我们从图中不难发现,\(|X_a-X_b|=f\),\(|Y_a-Y_b|=g\),因此 \(AB=\sqrt{f^2+g^2}=\sqrt{(X_a-X_b)^2+(Y_a-Y_b)^2}\),注意这里把绝对值符号去掉了,想想这是为什么。
因此,直接按照这个公式输出答案即可。
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
double Xa,Ya,Xb,Yb,AB;
cin>>Xa>>Ya>>Xb>>Yb;
AB=sqrt(pow(abs(Xb-Xa),2)+pow(abs(Yb-Ya),2));
cout<<fixed<<setprecision(3)<<AB;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号